СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ. СВОБОДНЫЕ ЕЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
Сложение гармонических колебаний
Одного направления и одинаковой частоты
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда возникает задача найти результирующее колебание, иными словами, колебания нужно сложить. Сложим гармонические колебания одного направления и одинаковой частоты:
,
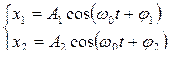воспользовавшись методом вращающегося вектора амплитуды, построим векторные диаграммы этих колебаний. Т.к. векторы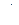 
и 
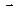вращаются с одинаковой угловой скоростью, то разность фаз (j2 - j1) между ними остаётся постоянной.
Очевидно, что уравнение результирующего колебания будет:
.
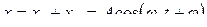В этом выражении амплитуда А и начальная фаза j соответственно задаются отношениями:
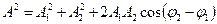. (10.1.1)
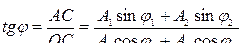. (10.1.2)
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания.
Амплитуда результирующего колебания зависит от разности фаз (j2 - j1) складываемых колебаний. Проанализируем это выражение в зависимости от разности фаз (j2 - j1).
1. 
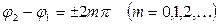В этом случае 
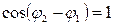и 
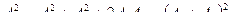, а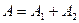 
, т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний.
Пусть, например, А1 = А2, тогда А = 2А1. Энергия каждого колебания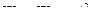 
, а энергия результирующего колебания в 4 раза больше энергии каждого из составляющих колебаний: 
.
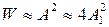2. Предположим теперь, что разность фаз равна:
.
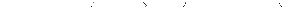В этом случае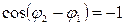 
и квадрат амплитуды результирующего колебания равен
,
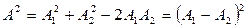а амплитуда равна: А = А1 – А2.
Если окажется, что А1 = А2, то амплитуда результирующего колебания будет равна нулю. Одновременно будет равна нулю энергия результирующего колебания.
Полученные результаты имеют ряд важных применений. Например, звуковые колебания, происходящие в определенной точке пространства от двух источников звука, могут усиливать друг друга или наоборот, ослаблять. При подходящих условиях в определенных точках пространства может оказаться, что «звук + звук = молчание».
С ложение взаимно-перпендикулярных колебаний
Одинаковой частоты
Шарик, подвешенный на легкой длинной пружине 
, конец которой закреплен на шарнире, может участвовать в двух взаимно перпендикулярных колебательных процессах (10.2.1).
Если возбудить одновременно оба колебания, то шарик будет двигаться по некоторой сложной траектории, форма которой зависит от соотношения частот и начальных фаз обоих колебаний.
Перейдем к сложению двух взаимно перпендикулярных гармонических колебаний одной и той же частоты 
, совершающихся вдоль координатных осей X и Y.
Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю.
Тогда уравнения колебания запишутся:
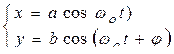, (10.2.1)
где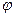 
- разность фаз обоих колебаний.
Эти уравнения представляют собой уравнение траектории в параметрической форме. Чтобы получить уравнение траектории в обычном виде нужно исключить параметр t.
Из уравнения (10.2.1):
;
.
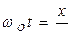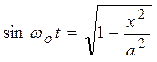Из уравнения (10.2.1):
.
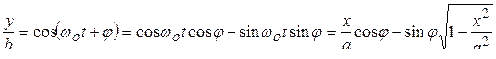После несложных преобразований получим
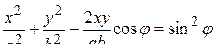. (10.2.2)
Это уравнение эллипса, оси которого ориентированы относительно координатных осей X и Y произвольно.
Рассмотрим некоторые частные случаи, представляющие физический интерес.
Разность фаз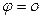 
(рис. 10.2.1) 
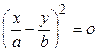, откуда и получается уравнение прямой: 
.
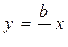Колеблющаяся точка движется по этой прямой, причем расстояние ее от начала координат равно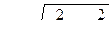 
.
Подставляя X и Y из уравнений (10.2.1) и (10.2.2) и учитывая, что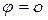 
, получим 
.
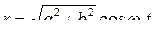Таким образом, результирующее движение является гармоническим колебанием вдоль прямой с частотой 
и амплитудой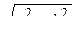 
.
Разность фаз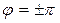 
(рис. 10.2.2), уравнение 
.
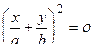Результирующее движение представляет собой гармоническое колебание вдоль прямой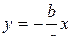 
.
3. При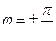 
, уравнение 
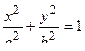(эллипс).
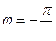
В момент t = 0 тело находится в точке 1. В последующие моменты X уменьшается, но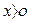 
, а координата Y становится отрицательной.
Движение совершается по часовой стрелке. При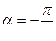 
уравнения 
.
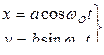Движение совершается против часовой стрелки (рис. 10.2.5).
Если взаимно перпендикулярные колебания происходят с различными периодами, то в результате сложения колебаний получаются траектории более сложной формы.
Эти траектории называются фигурами Лиссажу (рис. 10.2.5).
Дата добавления: 2019-09-13; просмотров: 160; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!