В ынужденные механические колебания

 

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора f ( t ), изменяющегося по гармоническому закону.

.

Если рассматривать механические колебания, то роль f ( t ) играет внешняя вынуждающая сила .

С учетом выражения для внешней вынуждающей силы, закон движения для пружинного маятника запишется в виде

или

     .                        (11.2.1)

Введем обозначения:

; ;  .

С учетом введенных обозначений уравнение движения запишется в виде

                .                          (11.2.2)

Получили неоднородное линейное дифференциальное уравнение второго порядка.

Решение уравнения (11.2.2) равно сумме общего решения  однородного уравнения 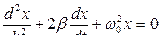 и частного решения неоднородного уравнения.

Частное решение будем искать в виде

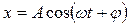  .                                      (11.2.3)

Подставляя (11.2.3) в уравнение (11.2.2) определим величины амплитуды и фазы из требования, чтобы уравнение (11.2.3) обратилось в тождество.

После нахождения первой и второй производной выражения (11.2.3) и подстановки их в (11.2.2), получим

.    (11.2.4)

Учитывая, что

уравнение (11.2.4) запишется в виде

. (11.2.5)

Чтобы это уравнение обратилось в тождество надо, чтобы в обеих частях были равны коэффициенты при cosωt и sinωt.

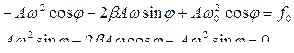
или

;                    (11.2.6)

.                      (11.2.7)

Из уравнения (11.2.7)

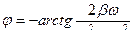         .           (11.2.8)

Возведя в квадрат и складывая уравнения (11.2.6) и (11.2.7), получим

;

,

;

 

; ,

откуда

                         ,                             (11.2.9)

где .

Уравнения (11.2.8) и (11.2.9) определяют фазу и амплитуду установившихся вынужденных колебаний.

Таким образом, частное решение неоднородного уравнения (11.1.2) имеет вид

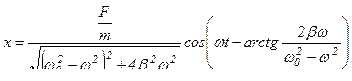               .       (11.2.10)

 

Графически вынужденные колебания представлены на рис. 11.2.1.

 

 

   

 

 

Если тело первоначально покоилось, а затем на него начала действовать вынуждающая сила , то оно начнет совершать вынужденные колебания, амплитуда будет возрастать, пока не достигнет значения, определяемого равенством (11.2.9), дальнейшее возрастание амплитуды прекращается.

Следовательно, в установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими; амплитуда и фаза колебаний, определяемая выражениями (11.2.8) и (11.2.9) также зависит от ω.

 

Механический резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты ω. Из формулы (11.2.1) следует, что амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Если частота ω₀ собственных колебаний не изменяется, а меняется частота вынуждающей силы, то при этом изменяется амплитуда вынужденных колебаний.

При некоторой определенной частоте амплитуда вынужденных колебаний достигает максимального значения. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой к собственной частоте колебательной системы называется резонансом.

Чтобы определить резонансную частоту ω_рез – частоту, при которой амплитуда смещения достигает максимума, - нужно найти максимум функции (11.2.9) или, что то же самое, минимум подкоренного выражения.

Продифференцировав подкоренное выражение по ω и, приравняв его нулю, получим условие, определяющее ω_рез.

;

или .

Это равенство выполняется при ω=0, ω , у которого только положительное значение имеет физический смысл. Следовательно, резонансная частота

.                                (11.3.1)

Подставим (11.3.1) в (11.2.9) получим выражение для амплитуды при резонансе

;

.                               (11.3.2)

Если сопротивление среды равно нулю, т.е. β = 0, то ω_рез = ω₀. в этом случае амплитуда вынужденных колебаний становится бесконечно большой.

Если , то А_рез никогда не достигает бесконечности, и максимум амплитуды получается при значениях .

На рис. 11.3.1 приведены зависимости амплитуды вынужденных колебаний от частоты при различных значениях β. Из (11.3.1) и (11.3.2) вытекает, что чем меньше β, тем выше и правее лежит максимум данной кривой. При  все кривые достигают одного и того же предельного значения равного , которое называют статическим отклонением. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величиной F ₀ .

При  все кривые асимптотически стремятся к нулю, так как при большей частоте сила, так быстро изменяет свое направление. Поэтому  колебательная система не успевает заметно сместиться из положения равновесия.

 

                 

Рис. 11.3.1

 

Явление резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения.

С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так радиотехника, прикладная акустика, электротехника используют явление резонанса.

Лекция 12

---

Дата добавления: 2019-09-13; просмотров: 210; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!