О сновные понятия и определения
Основными характеристиками гармонической волны являются период (частота) и длина волны (рис. 13.2.1).
1. Период волны Т(с) – время, за которое совершается один полный цикл колебаний в осцилляторе .
Следовательно, за период Т волна дойдет до частицы, колеблющейся в той же фазе, то есть Dj = 2 p.
2. Вместо периода Т часто пользуются частотой n, равное числу колебаний в единицу времени
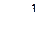(с-1). (13.2.1)
3. Длина волны l (м) – расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, то есть путь, пройденный волной за период
l = u Т (13.2.2)
или
,
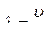где u - скорость распространения волны.
Соотношения (13.2.1) и (13.2.2) справедливы для гармонических волн любой природы.
4. В теории волн пользуются также понятием волнового вектора (волновое число).
Волновой вектор 
по абсолютной величине равен числу длин волн на отрезке 2p
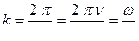; (13.2.3)
.
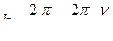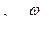так как 
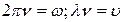и ориентирован в направлении распространения волны.
5. Геометрическое место точек, колеблющихся в данный момент времени в одинаковой фазе, называется волновой поверхностью (поверхность равной фазы).
6. Поверхность, которая отделяет колеблющиеся частицы от частиц, еще не пришедших в колебание (в общем случае: передний край волны непосредственно граничит с невозмущенной средой), называется фронтом волны.
|
|
|
Иначе говоря, геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны.
Волновое движение, при котором волновой фронт перемещается с конечной скоростью, называется бегущей волной.
Волновые поверхности остаются неподвижными всегда. Они могут быть любой формы.
В простейшем случае – плоскость или сфера. Такие волны называются соответственно плоскими или сферическими.
В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей; в сферической волне – систему концентрических сфер.
|
|
|
|
|
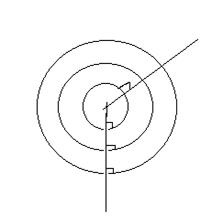
Плоскость, проходящая через направление колебаний и направление распространения, называется плоскостью колебаний или плоскостью поляризации.
Волна, имеющая одну такую плоскость, называется линейнополяризованной (или плоско-поляризованной).
Основной задачей изучения плоских волн является установление закона изменения во времени и пространстве физических величин, характеризующих тот или иной тип волнового процесса.
|
|
|
У равнение плоскополяризованной бегущей волны.
В олновое уравнение
С бегущей волной связан перенос энергии, импульса и других характеристик.
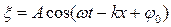. (13.3.1)
Уравнением волны называется зависимость смещение (x) колеблющейся частицы от координат (x, y, z) и времени (t)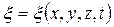 
,
где x, y, z –координаты равновесного положения частицы.
|
x = x(х, t).
В этом случае волновые поверхности будут перпендикулярны к оси х. Рассмотрим некоторую точку В, находящуюся от источника колебаний на расстоянии х.
Пусть колебания точек, лежащих в плоскости х, равны нулю, тогда уравнение волны имеет вид
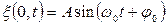или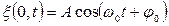 
.
Если волна незатухающая, то амплитуды колебаний всех точек одинаковы и равны А.
Для того чтобы пройти путь от плоскости х = 0 до плоскости, соответствующей произвольному значению х, волне требуется время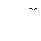 
, где u - скорость распространения волны.
Следовательно, колебания частиц, лежащих в плоскости х, будут отставать по времени на t от колебаний частиц, лежащих в плоскости х = 0, т.е. будут иметь вид
|
|
|
.
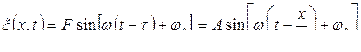Итак, уравнение плоско-поляризованной волны (и продольной и поперечной), распространяющейся вдоль оси х, имеет вид
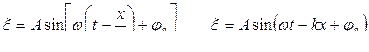(13.3.2)
или
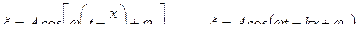, (13.3.3)
где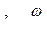 
.
Волна, распространяющаяся в сторону убывания х, описывается уравнением
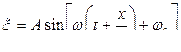, для нее 
.
Начальная фаза волны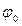 
0пределяется выбором начала отсчета х и t. При рассмотрении одной волны начала отсчета времени, и координаты обычно выбираются так, чтобы 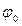= 0. При совместном рассмотрении нескольких волн сделать так, чтобы для всех них 
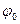= 0, как правило, не удается. Выражение
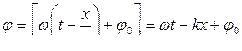(13.3.4)
называется фазой волны.
Предположим, что при волновом процессе фаза постоянна, т.е.
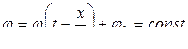. (13.3.5)
Это выражение определяет связь между временем t и координатой х той точки, в которой фаза имеет фиксированное значение.
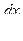- скорость, с которой перемещается данное значение фазы.
Продифференцируем выражение (13.3.5)
;
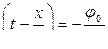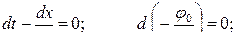
откуда
. (13.3.6)
|
|
|
Скорость распространения волны u в уравнениях (13.3.5) и (13.3.6) есть не что иное, как скорость перемещения фазы волны, поэтому ее называют фазовой скоростью.
Для продольной волны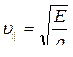 
,
где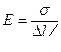 
- модуль Юнга, r - плотность среды, 
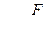- напряжение.
Для поперечной волны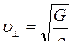 
,
где G – модуль сдвига.
Таким образом, u зависит от свойств среды.
Для звука в газ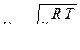е 
, где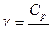 
.
Для звука в воздухе u = 20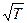 
, м/с.
Кроме фазовой скорости различают еще групповую скорость, которую вводят тогда, когда реальная волна не может быть представлена одним гармоническим уравнением (13.3.2), а является суммой группы синусоидальных волн.
Групповая скорость – скорость движения группы или дуга волн, образующих в каждый момент времени локализованный (сконцентрированный) в пространстве волновой пакет.
С групповой скоростью происходит перенос энергии волны. Все методы измерения скоростей распространения волн, связанные с запаздыванием сигналов (в том числе скорости света), дают групповую скорость. Именно оно фигурирует при измерении дальности в гидро- и радиолокации, при зондировании ионосферы, в системах управления космическими объектами и т.д. u ср £ u фаз; для фазовых скоростей ограничений не существует.
В олновое уравнение
Уравнения волны (13.3.2) и (13.3.3) есть решения общего дифференциального уравнения с частными производными, описывающего процесс распространения возмущения в среде. Такое уравнение называется волновым.
Продифференцируем (13.3.2) дважды по времени t и дважды по координате х. Положим 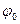= 0.
;
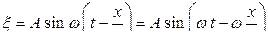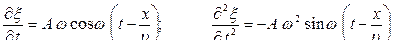; (13.4.1)
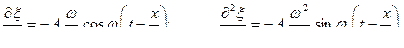(13.4.2)
Уравнение (13.4.5?) – волновое уравнение плоско-поляризованной волны. Для пространственной волны волновое уравнение имеет вид
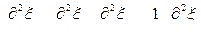. (13.4.3)
Это уравнение можно записать в виде
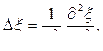(13.4.4)
где D - оператор Лапласа – сумма вторых частных производных по координате от функции.
Волновому уравнению (13.4.4, 13.4.3) удовлетворяют (13.3.4, 13.3.5, 13.3.6).
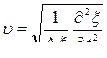- фазовая скорость волны. (13.4.5)
Если изменение какой-либо физической величины (механической, тепловой, электрической, магнитной и т.д.) отвечает уравнению (13.4.3), то это означает, что колебания соответствующей физической величины распространяются в виде волны со скоростью, определяемой по формуле (13.4.6). В этом случае x (х, y, z) - функция, характеризующая возмущение среды в точке с координатами х, y, z в момент времени t (Е и Н для электромагнитной волны).
Дата добавления: 2019-09-13; просмотров: 156; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!