Гармонический осциллятор. маятники

Физическая система, совершающая колебания, называется осциллятором. Гармоническим осциллятором называется система, совершающая колебания описываемая уравнением

.

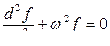Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур и др.

Моделью классического гармонического осциллятора является колеблющейся шарик массой m, подвешенный на пружине с коэффициентом упругости k.

Линейный гармонический осциллятор является одной из важных моделей, используемых атомной физикой. В частности, к осциллятору сводится задача о колебаниях молекул. Наиболее часто встречающийся электрический осциллятор – колебательный контур, содержащий индуктивность и емкость. Колебания напряженностей электрического и магнитного полей в плоской электромагнитной волне также можно описывать с помощью понятия «осциллятор».

Понятие «осциллятор» играет важную роль в теории теплоемкости твердых тел, где колебания кристаллической решетки описываются совокупностью «осцилляторов», а также в теории колебательных спектров молекул.

 

Пружинный маятник

 

Пружинный маятник – груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = -kx, где k – коэффициент упругости (жесткость пружины). Уравнение движения маятника описывается вторым законом Ньютона:

;

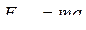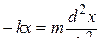
   или    ;

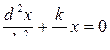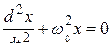                                   .                                   (10.3.1)

Уравнение (10.3.1) - есть дифференциальное уравнение 2-го порядка, описывающее гармоническое колебательное движение пружинного маятника. Оно имеет два решения:

.

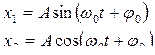Собственная циклическая частота

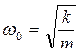                   .                                      (10.3.2)

Период

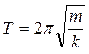                                  .                                     (10.3.3)

Потенциальная энергия пружинного маятника равна:

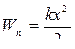                                  .                                      (10.3.4)

 

Физический маятник

 

Физический маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, не проходящей через центр масс C тела (рис. 10.3.1).

Если маятник отклонен из положения равновесия на некоторый угол a, то в соответствии с уравнением динамики вращательного движения твердого тела, момент возвращающей силы 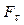 можно записать в виде.

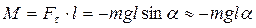.       (10.3.5)

 

С другой стороны, согласно основному уравнению динамики вращательного движения:

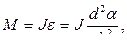                                  (10.3.6)

где J – момент инерции маятника относительно оси, проходящей через точку 0; l – расстояние между точкой подвеса и центром масс маятника; 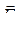 - возвращающая сила.

Знак «минус» обусловлен тем, что направления 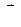 и a всегда противоположны.

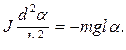                                        .                                      (10.3.7)

Это уравнение можно записать в виде:

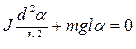 или

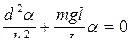                    .                                (10.3.8)

Полученное выражение является уравнением гармонического колебания физического маятника. Сравнивая с уравнением 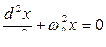, определим собственную циклическую частоту

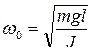                             .                                     (10.3.9)

Одним из решений уравнения (10.3.8) является выражение

                                                   (10.3.10)

где a_т – амплитуда.

Период колебания

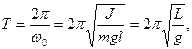                                                (10.3.11)

где 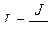 - приведенная длина физического маятника.

Из уравнения (10.3.11) следует, что при малых отклонениях физический маятник совершает гармонические колебания.

Точка 0' на продолжении прямой 0С, отстающая от оси подвеса на расстоянии приведенной длины L, называется центром качаний физического маятника. Точка подвеса 0 и точка качания 0' обладают свойством взаимозаменяемости: если ось подвеса будет проходить через центр качаний, то точка 0 прежней оси подвеса станет центром качаний, а период колебаний физического маятника не изменится.

 

Математический маятник

Математический маятник – идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести (рис. 10.3.2).

Определим период колебания математического маятника длины l.

Пусть маятник отклонен от вертикали на угол 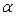. Сила, возвращающая груз маятника в положение равновесия, есть составляющая                 

.

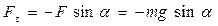Для малых углов 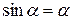, тогда

 

Знак (-) означает, что сила F 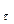направлена в сторону, противоположную той, в которую отсчитываются положительные углы .

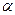Обозначим угловое ускорение через 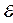, тогда касательное к траектории, т.е. ускорение . По 2-му закону Ньютона  или .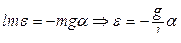

Обозначив 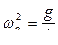, получим:  или .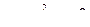

Полученное уравнение примет вид .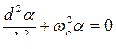

Его решение:  

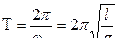; где .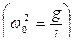

 

Подставим 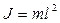 в выражение для периода 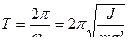, получим выражение для периода малых колебаний математического маятника: .

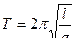Сравнивая формулы 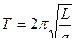 и 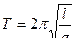, видим, что если приведенная длина L физического маятника равна длине математического маятника, то их периоды колебаний равны.

Следовательно, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

При небольших амплитудах период колебаний не зависит от амплитуды и массы маятника, а определяется только его длиной.

 

---

Дата добавления: 2019-09-13; просмотров: 237; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!