РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ

И В ПОЛЕ ПОТЕНЦИАЛЬНЫХ СИЛ

Распределение максвелла

В результате столкновения молекул друг с другом и со стенками сосуда молекулы имеют самые различные значения скоростей. Поскольку тепловое движение молекул газа беспорядочное, то в состоянии равновесия все направления скоростей молекул при тепловом движении равновероятны.

Однако несмотря на беспорядочность движения, распределение молекул по скоростям имеет строгую закономерность. Эта закономерность из-за большого числа хаотически движущихся молекул носит статистический характер.

Задача о распределении молекул газа по скоростям была поставлена и решена К. Максвеллом (англ. 1831 – 1879 г.) в 1860 году.

Допустим, что в единице объема содержится N молекул газа и внешние силовые поля (например, сила тяжести), действующее на газ, отсутствуют. Рассмотрим так называемое пространство скоростей ( 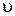- пространство), в котором прямоугольными координатными осями являются компоненты скорости (имеются в виду проекции вектора скорости на оси взятые в обычном пространстве).

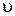Очевидно, что в -пространстве скорости каждой молекулы изображаются точкой, которая называется скоростной точкой. Вследствие равно вероятности всех направлений движения расположение точек относительно начала координат будет сферически симметричным. Изучая распределение молекул по скоростям, нельзя ставить вопрос о числе молекул, которые обладают точно заданной скоростью 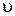. Таких молекул в каждый данный момент времени вообще может не оказаться, так как число возможных значений скоростей бесконечно большое, а число молекул конечно. Поэтому правильно ставить вопрос так: какое число dN молекул однородного одноатомного идеального газа из общего числа его молекул N имеет при данной температуре скорости, заключенные в интервале от u до . Точки, изображающие скорости, величина которых заключена в пределах от u до , попадают в область, лежащую между сферами радиусов u и (рис. 3.1.1). Объем этой области равен .

Обозначим через dN _u число молекул в единице объема, имеющих скорости в заданном интервале от u до . Очевидно, что, чем больше этот интервал, т.е. чем больше объем , тем больше будет молекул со скоростями в этом интервале (dN _u ~ ). Кроме того, это число молекул dN _u пропорционально общему числу молекул в единице объема N ( 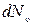~ N ), обладающих всеми скоростями (из большего числа N можно больше выбрать dN _u).

Оказывается, что число молекул зависит еще и от того, каким скоростям принадлежит выбранный интервал скоростей:

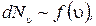
где f (u) – функция, зависящая от скорости.

Окончательно можно записать

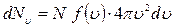. (3.1.1)

Разделив на N, получим вероятность 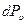того, что скорость некоторой молекулы окажется в пределах от u до :

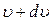(3.1.2)

или

, (3.1.3)

где - функция распределения молекул по скоростям.

С учетом того, что выражение (3.1.1) запишется так

, (3.1.4)

откуда

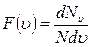при d u = 1, .

Таким образом, функция распределения показывает, какая доля из общего числа молекул в единице объема при данной температуре обладает скоростями единичного интервала вблизи заданной скорости (u).

Вид функции F(u) был получен К. Максвеллом с помощью методов теории вероятности.

Функция распределения имеет окончательный вид

. (3.1.5)

График функции распределения при T = const как произведение двух переменных множителей и представлен на рис. 3.1.2.

Рис. 3.1.2

Поскольку при возрастании скорости u множитель 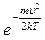убывает быстрее, чем растет множитель , функция распределения F(u), начинаясь в нуле из-за , достигает максимума и затем асимптотически приближается к оси абсцисс, т.к. число молекул, неподвижных (u = 0) и движущихся с бесконечной скоростью (u = ¥), равно нулю.

Доля молекул в единице объема, обладающих скоростями, лежащими в интервале от u до 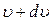, т.е. , численно равна площади заштрихованного на графике столбика.

Наглядно видно, что для одинакового интервала эта доля молекул различна для разных областей скоростей .

Вся площадь под кривой численно равна доле молекул в единице объема, обладающих всеми скоростями от 0 до ¥. Очевидно, что эта доля равна единице или 100 %.

Подставляя (3.1.5) в (3.1.4)

. (3.1.6)

Данное выражение определяет число молекул единицы объема обладающих скоростями вблизи скорости u.

Из этой формулы можно перейти от распределения молекул по скоростям к распределению Максвелла по кинетическим энергиям поступательного движения молекул.

В формулу (3.1.6) подставляем и , при этом мы учли, что кинетическая энергия поступательного движения .

Получим

где dN _u - определенное число молекул в единице объема, кинетическая энергия поступательного движения которых имеет значения, заключающиеся в пределах от W_k до W_k + dW_k. Таким образом, распределение молекул по значениям кинетической энергии характеризуется функцией:

где - нормировочный (коэффициент) множитель.

Максвелловское распределение – статистический закон, верный с тем большей точностью, чем больше число молекул N находится в единице объема газа. Это распределение является равновесным, т.е. ему подчиняются частицы, представленные сами по себе (внешние воздействия отсутствуют). Если газ каким-либо внешним воздействием вывести из равновесного состояния, распределение молекул будет иным. При переходе к равновесию (внешнее воздействие устранено) в результате столкновений между молекулами снова устанавливается именно максвелловское распределение.

3.2 . н аиболее вероятная скорость u _вер

Скорость, отвечающая максимуму функции распределения молекул по скоростям F(u), называется наиболее вероятной скоростью u _вер.

Очевидно, что скоростями интервала вблизи u _вер обладает наибольшая доля молекул.

Рис. 3.2.1

Наиболее вероятная скорость u _вер находится из условия максимума функции распределения F(u), т.е. из условия:

Возьмем первую производную от выражения (3.1.5) по u, опустив постоянные множители, и приравняем получившееся выражение к нулю.

Этому уравнению удовлетворяют три значения скорости. Значения u = 0 и u = ¥ соответствуют минимумам F(u). Третье значение получим из условия: 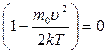. Откуда и получим искомую наиболее вероятную скорость. Итак:

(3.2.1)

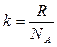т.к. и .

3.3. с редняя скорость < u > .

(средняя арифметическая скорость)

Среднюю скорость молекул <u > можно получить из формулы определения средней величины:

При интегрировании необходимо учесть, что (табличный интеграл), , тогда интегрирование уравнения (3.3.1) дает

После упрощения получим

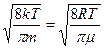, (3.3.1)

т.к. .

3.4. с редняя квадратичная скорость

Средняя квадратичная скорость была получена ранее. Она характеризует среднюю кинетическую энергию поступательного движения молекулы:

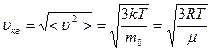. (3.4.1)

Средняя квадратичная скорость может быть получена и из распределения Максвелла. Из формулы определения средней величины:

В соответствии со значением интеграла , , получим

после упрощения получим

тогда

= ,

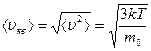что соответствует формуле (3.4.1).

Таким образом, скорости, характеризующие состояние идеального газа:

=1,13 ,

=1,22 .

Сравнивая формулы (3.2.1), (3.3.1) и (3.4.1) мы видим, что u _вер <u> u _кв

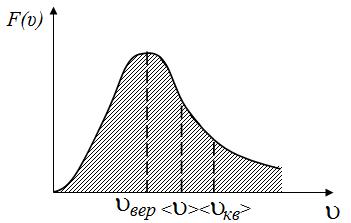
Рис. 3.4.1

Из формул (3.2.1), (3.3.1) и (3.4.1) следует, что скорости u _вер, <u >, u _кв зависят от температуры и массы молекул m ₀ (или молярной массы m).

При увеличении температуры (или уменьшении молярной массы газа m) максимум кривой F(u) смещается вправо и становится ниже (рис. 3.4.1).

Это объясняется тем, что при увеличении Т (или уменьшении m) скорости молекул увеличиваются, а площадь под кривой функции по-прежнему должна быть равна единице общее число молекул в единице объема не меняется.

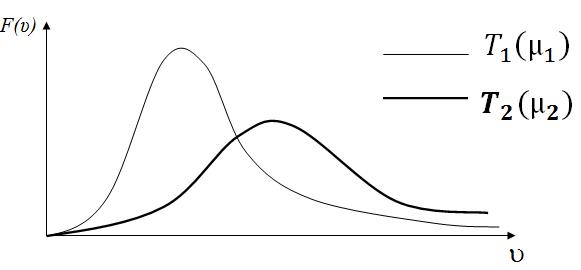
Рис. 3.4.2

На рис. 3.4.2 сопоставлены две кривые распределения молекул по скоростям, которые можно трактовать как относящиеся к различным температурам Т₁ и Т₂ для одного и того же газа (m = const), либо как относящиеся к различным газам с m₁ и m₂ при одинаковой температуре (Т = const), причем концентрации этих газов равны ( ).

О пыт штерна

В 1920 г. немецкий физик О. Штерн экспериментально измерил скорости теплового движения молекул газа, подтвердив закон распределения Максвелла. Схема опыта состояла в следующем (рис. 3.5.1).

Два коаксиальных цилиндра вращались с одинаковой угловой скоростью w. По оси прибора была натянута платиновая проволока, покрытая слоем серебра. При нагревании проволоки электрическим током с поверхности испарялись атомы серебра.

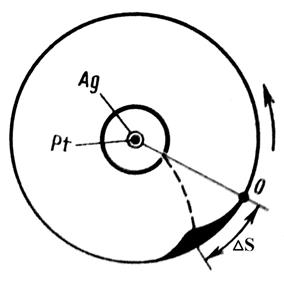
Рис. 3.5.1

При нагревании проволоки электрическим током с поверхности испарялись атомы серебра. Скорости испарившихся атомов соответствовали температуре проволоки. В приборе был создан вакуум, чтобы атомы серебра не испытывали столкновений с молекулами воздуха. Внутренний цилиндр имел узкую продольную щель, через которую проходил узкий пучок атомов серебра. Достигнув поверхности внешнего цилиндра, атомы серебра оседали на ней.

При вращении прибора след осадка атомов серебра на поверхности внешнего цилиндра сместится на некоторую величину DS. Это произойдет, потому что за время, пока атомы пролетают зазор между цилиндрами, прибор успевает повернуться на некоторый угол Dj. Величина смещения следа пучка , где R – радиус внешнего цилиндра.

Смещение DS можно связать с угловой скоростью вращения цилиндра w, геометрией прибора и скоростью атомов. Пусть Dt – время пролета атомами серебра расстояния между цилиндрами (R – r) (r – радиус внутреннего цилиндра):

За это время цилиндры повернуться на угол Dj, так что , тогда смещение:

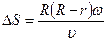а скорости атомов:

Таким образом, измеряя смещение следа DS и скорости вращения прибора w, можно экспериментально определить скорость атомов. Результаты опыта Штерна подтвердили правильность оценки средней скорости атомов, которая вытекает из распределения Максвелла.

Вследствие теплового движения молекул скорости отдельных атомов серебра различны, и осадок на большем цилиндре дает размытое изображение щели (рис. 3.5.1). Кроме того, толщина слоя осадка в разных местах оказывается различной. При исследовании толщины слоя осадка в зависимости от угла поворота Dj получено соответствие распределения молекул по скоростям. Наибольшая толщина осадка соответствовала тому месту, куда прилетали атомы со скоростью u _вер. Результаты подсчета u _вер из опыта оказались близкими результатами, вычисленными по формуле

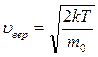Р аспределение больцмана

Распределение Больцмана описывает распределение частиц идеального газа, хаотически движущихся во внешнем силовом (потенциальном) поле. В состоянии теплового равновесия температура Т должна быть одинакова по всему объему газа (T = const). В противном случае возникли бы потоки тепла, и состояние газа не было бы равновесным. Таким образом, газ находится в механическом равновесии.

Пусть в направлении оси о z на каждую молекулу газа действует сила (например, сила тяжести) (рис. 3.6.1).

Мысленно выделим объем газа в виде цилиндра с площадью основания S и высотой dz, настолько малой, чтобы можно было в пределах этой высоты силу считать одинаковой, т.е. силовое поле однородным.

Тогда на все частицы, находящиеся в объеме цилиндра действует результирующая сила, равная (n – концентрация газа). Так как газ находится в состоянии механического равновесия (нет потоков), то эта сила должна быть уравновешена разностью сил давления на основания:

Таким образом,

или

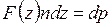. (3.6.1)

От давления р перейдем к концентрации, используя соотношение , откуда

. (3.6.2)

Используя (3.6.2), выражение (3.6.1) перепишем как

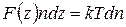
или

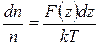Произведение , где A – работа потенциальных сил, которая равна убыли потенциальной энергии :

Отсюда

Подставляя в формулу для , получим

Проинтегрируем, считая, что n – концентрация молекул в том месте пространства, где потенциальная энергия молекулы имеет значение W_p, а n_o – концентрация молекул в том месте пространства, где потенциальная энергия молекулы равна нулю.

Таким образом,

; ;

;

. (3.6.3)

Выражение (3.6.3) называется законом распределения Больцмана. Этот закон учитывает распределение молекул в зависимости от их потенциальной энергии в любом силовом поле. Из формулы (3.6.3) следует, что молекулы располагаются с большой концентрацией там, где меньше их потенциальная энергия, и, наоборот, с меньшей концентрацией – в местах, где их потенциальная энергия больше.

В то время как закон Максвелла дает распределение частиц по значениям кинетической энергии, закон Больцмана дает распределение частиц по значениям потенциальной энергии. Для обоих распределений характерно наличие экспоненциального множителя, в показателе которого стоит отношение кинетической или соответственно потенциальной энергии одной молекулы к величине kT, определяющей среднюю энергию теплового движения молекулы.

Учитывая, что , закон распределения Больцмана примет вид

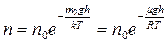. (3.6.4)

Б арометрическая формула

Формула (3.6.3) распределения Больцмана позволяет получить выражение зависимости атмосферного давления от высоты.

Атмосферное давление р на какой-либо высоте h обусловлено весом вышележащих слоев газа. Молекулы воздуха находятся в поле тяготения Земли, и потенциальная энергия молекулы:

Кроме того, учитывая, что и 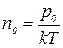, выражение (3.6.3) запишем в виде

. (3.7.1)

Формула (3.7.1) называется барометрической формулой. Из барометрической формулы следует, что давление газа убывает с высотой по экспоненциальному закону. Этой формулой пользуются для определения высоты над землей самолетов, гор и т.д. (с учетом поправки на температуру). Кроме того, из формулы (3.7.1) видно, что убывание давления газа с высотой зависит от молярной массы m: чем тяжелее газ (больше m), тем быстрее убывает его давление с высотой. Процентное содержание кислорода на больших высотах значительно меньше, чем у поверхности Земли.

Рис. 3.7.1

На рис. 3.7.1 изображены две кривые, соответствующие барометрической формуле (3.7.1). Эти кривые можно трактовать как соответствующие разным m (при одинаковой Т), либо как отвечающие разным Т (при одинаковой m).

В формуле (3.7.1) - давление газа на высоте h₀= 0 м, 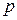- на высоте . Если с помощью барометра измерить давление 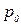и , то по формуле (3.7.1) можно определить высоту

Поэтому (3.7.1) называется барометрической формулой. Барометр, специально проградуированный для отсчета высоты над уровнем моря, называется альтиметром. Он широко применяется в авиации, при восхождении на горы и т.п.

О пыт перрена

Формула (3.6.3) распределения Больцмана была применена в 1906 г. французским физиком Ж. Перреном для броуновских частиц и использована для определения числа Авогадро N_A. Броуновские частицы находятся в беспорядочном движении под влиянием ударов молекул. Исходя из общих соображений о характере беспорядочных ударов, можно показать, что средняя кинетическая энергия одной броуновской частицы равна средней кинетической энергии молекулы при данной температуре Т. Таким образом, совокупность броуновских частиц в точности воспроизводит модель молекулярно-кинетической структуры газа; только в этой модели «молекулы» так велики, что их можно видеть в микроскоп, скорости же их движения малы из-за большой по сравнению с отдельной молекулой массы.

Совокупность броуновских частиц подчиняется всем газовым законам, в том числе и закону распределения Больцмана .

Перрен применил следующий метод: кювета заполняется эмульсией, в которой находятся во взвешенном состоянии броуновские частицы.

Эмульсия рассматривалась в микроскоп с малой глубиной изображения (рис. 3.8.1).

Рис. 3.8.1

Для броуновских частиц, находящихся в жидкости, поле тяжести ослаблено архимедовой подъемной силой. В установившемся состоянии концентрация частиц по закону Больцмана:

В поле тяжести потенциальная энергия частицы на высоте h равна , где Р – вес броуновской частицы с учетом силы Архимеда:

где r - плотность вещества частицы, r_о – плотность жидкости, V – объем частицы.

После упрощения получим

И тогда для броуновских частиц концентрация на высоте h равна

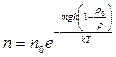Передвигая объектив микроскопа, его можно было фокусировать на различные слои эмульсии и, таким образом, замечать изменение числа частиц с высотой. Перрен производил мгновенные фотоснимки в микроскоп и по ним определял число частиц в поле зрения различных слоев эмульсии.

где N₁, N₂ – число частиц в поле зрения на высоте h₁ и h₂ соответственно; N₀ – число частиц на высоте, принятой за нулевую.

Разделив N₁ на N₂, получим

Так как , то

и .

Откуда расчетная формула числа Авогадро:

Разность высот определялась сдвигом микроскопа с помощью микрометрического винта. Масса сферической броуновской частицы m непосредственно выражается через ее радиус r и плотность r вещества, из которого она состоит:

где радиус r измерялся с помощью микроскопа с отсчетным объективом.

Полученное Перреном на различных эмульсиях и при различных температурах значение N_A находилось в пределах от моль^-1 до моль^-1.

Дальнейшие опыты позволили определить число Авогадро с точностью до 1 %. В настоящее время для числа Авогадро применяется значение моль^-1. Таким образом, значение, полученное Перреном, находится в хорошем согласии со значениями, полученными другими методами, что доказывает применимость к броуновским частицам распределения Больцмана.

Лекция 4

Дата добавления: 2019-09-13; просмотров: 519; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!