Лекция 4. Линейные электрические цепи при периодических негармонических воздействиях

4.1 Периодические несинусоидальные токи, напряжения и ЭДС. Понятие о гармоническом анализе

В предыдущей лекции были рассмотрены линейные электрические цепи при периодических синусоидальных напряжениях и токах. На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи (см. лекцию 7) обусловливает искажение формы токов даже при синусоидальных ЭДС источников.

В общем случае характер изменения величин может быть периодическим, почти периодическим и непериодическим. В данной лекции рассматриваются линейные электрические цепи только с периодическими переменными (токами, напряжениями, ЭДС).

Периодическими несинусоидальными токами (напряжениями, ЭДС) называют электрические токи (напряжения, ЭДС), изменяющиеся по периодическому несинусоидальному закону.

Пример периодических несинусоидальных величин демонстрируют временные диаграммы токов i(t ), приведенные на рисунке 4.1

Рисунок 4.1 – Временные диаграммы периодических несинусоидальных токов

Анализ электрических цепей при периодических несинусоидальных воздействиях

проводят путем представления функций i = i(t ), u = u(t ), e = e(t ), то есть токов,

напряжений и ЭДС, в виде рядов Фурье. Раздел математики, который изучает возможности такого представления, называется гармоническим анализом.

4.2 Представление несинусоидальных токов, напряжений и ЭДС в виде рядов Фурье

Периодический несинусоидальный сигнал s(t ) (ток, напряжение, ЭДС)

характеризуется промежутком времени (периодом) T , таким что

s(t ) = s(t ± T ). (4.1)

Если функция s(t ), задающая этот сигнал, удовлетворяет условиям Дирихле (имеет

конечное число разрывов 1-го рода и конечное число экстремумов), она может быть представлена тригонометрическим рядом Фурье

s(t ) = A0 +å A km si n(k w t +y k ). (4.2)

k =1

Величина A0 в выражении (4.2) называется постоянной составляющей или нулевой

гармоникой сигнала, функция A1m sin(w t +y1 )

— основной синусоидой или первой

гармоникой, функции A km sin(k w t +y k ) при k > 1 — высшими гармониками, а вся

совокупность гармоник — спектром сигнала. Частота

w = 2p f

= 2p T

называется

основной частотой (частотой следования), коэффициенты

A km

и y k

— амплитудами и

начальными фазами гармоник. Совокупность коэффициентов

A km

образует

амплитудный спектр сигнала, совокупность коэффициентов y k

— его фазовый спектр.

Их распределение по частотной оси отображают спектральными диаграммами

(спектрограммами).

Для вычисления коэффициентов ряда Фурье его гармонические составляющие запишем в форме

A km sin(k w t +y k ) = A km cos y k sin k w t + A km sin y k cosk w t =

= B k sin k w t + C k cos k w t .

Таким образом,

s(t ) = A0 +å(B k si n k w t + C k cosk w t ). (4.3)

k =1

Постоянная составляющая интегралов

A0 и коэффициенты B k

и C k

определяются с помощью

A = 1 s(t )dt ,

0 T

(T )

B = 2 s(t )sin k w tdt ,

k T

(T )

C = 2 s(t )cos k w tdt , (4.4)

k T

(T )

где интегрирование проводится на интервале периода T , например, (- T

и т.д.

2;T

2), (0;T )

Установим связь между коэффициентами

A km

и y k

формулы (4.2) и

коэффициентами B k

то

и C k

формулы (4.3). Поскольку

B k = A km cos y k ,

C k = A km sin y k ,

B2 + C 2 = A2 (cos2y

+ sin2y

)= A2 ,

tg y

= sin y k = C k

k k km k

и, следовательно,

k km

k cos y B

A km = ,

y = arctg C k . (4.5)

Формулы (4.2) – (4.5) составляют основу гармонического анализа, согласно которому, любой периодический негармонический сигнал можно представить как

совокупность постоянной составляющей A0 и бесконечного числа гармонических

составляющих A km sin(k w t +y k ). Так, например, для негармонического тока,

напряжения и ЭДС допустимы следующие представления:

i = I0 +åI km si n(k w t +y ik ),

k =1

u = U0 +åU km si n(k w t +y uk ),

k =1

e = E0 +åE km si n(k w t +y ek ), (4.6)

k =1

где i , u , e — мгновенные значения этих величин,

I0 ,

U0 , E0

— постоянные

составляющие, гармоник.

I km , U km ,

E km

— амплитуды гармоник, y ik , y uk , y ek

— начальные фазы

Примечание – Функция

s(t ), определяющая негармонический сигнал, как и

всякая периодическая функция (независимо от свойств симметрии), обладает следующими свойствами:

1) сумма, разность, произведение и частное периодических функций периода T

есть периодическая функция периода T ;

2) если функция s(t ) имеет период T , то функция s = s(at ) ( a ¹ 0 ) имеет период

T a ;

3) определенный интеграл от периодической функции s(t ) с периодом T по

любому отрезку длиной T имеет одно и то же значение, то есть при любом t

справедливо равенство

òs(t )dt =

t+T

òs(t )dt . (4.7)

4.3 Действующее и среднее значение периодической несинусоидальной величины

Периодический несинусоидальный ток по аналогии с током синусоидальным может быть охарактеризован эффективным или действующим значением. В разделе 3.2 действующее значение периодической величины определялось в общем виде (3.7) как ее среднеквадратичное значение за период:

I = . (4.8)

Используя представление негармонического тока выражением

i(t )

рядом Фурье (4.2), т.е.

i = I0 +åI km si n(k w t +y ik ), (4.9)

k =1

подынтегральную функцию i2 (t ) в формуле (4.8) запишем следующим образом:

i2 (t ) = I 2 + I

0å

k =1

I km

sin(k w t +y ik

)+å

k =1

2 sin2 (k w t +y )+

¥ ¥

+ ååI km I nm si n(k w t +y ik )si n(n w t +y in ). (4.10)

k =1

n=1 k ¹n

Подставляя соотношение (4.10) в формулу (4.8), после несложных преобразований получим

0 2å km

или

I 2 = I 2 + 1 I 2

k =1

I = =

, (4.11)

где

I1 = I1m

, I2 = I2m

, K ,

I k = I km

K — действующие значения гармоник,

представляющих ряд (4.9).

Таким образом, действующее значение периодического несинусоидального тока согласно (4.11) равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник.

Аналогичным образом, исходя из представления напряжений и ЭДС, т.е. функций

u(t ) и e(t ), рядами Фурье (4.6), на основании формул (3.8) можно доказать, что

действующие значения несинусоидальных напряжений и ЭДС равны:

U = , E =

, (4.12)

где

U k = U km

и E k

= E km

( k = 1,¥ ) — действующие значения гармоник

напряжения и ЭДС.

Средним значением периодической несинусоидальной величины (средневыпрямленным значением) называют ее среднее значение за половину периода. Так, например, среднее значение силы тока

I = 2

ср T

T 2

òi(t )dt . (4.13)

Так же определяются средние значения напряжения и ЭДС:

U = 2

ср T

T 2

òu(t )dt ,

E = 2

ср T

T 2

òe(t )dt . (4.14)

Отметим, что любой из интегралов (4.13), (4.14) равен среднему по модулю

значению величины за период, если каждая из этих величин, например, i(t ), имеет одинаковые положительные и отрицательные полуволны:

I ср = 1 ò i(t )dt = 2

T 2

òi(t )dt .

T T

0 0

Примечания

1 Из формул (4.6), представляющих разложения периодических токов, напряжений и ЭДС в ряды Фурье, и из выражений (4.4) для коэффициентов этих

разложений следует, что средние за период значения несинусоидальных величин совпадают с нулевыми гармониками (с постоянными составляющими):

I0 = 1 òi(t )dt ,

U0 = 1 òu(t )dt ,

E0 = 1 òe(t )dt .

2 Измерение несинусоидальных токов, напряжений и ЭДС приборами различных систем может давать неодинаковые результаты.

Приборы электродинамической, электромагнитной и тепловой систем реагируют на действующие значения измеряемой величины. Магнитоэлектрические приборы сами по себе измеряют постоянную составляющую, а с выпрямителями — среднее по модулю значение.

4.4 Коэффициенты, характеризующие форму периодических несинусоидальных величин

При оценке формы периодических несинусоидальных величин используют

следующие характеристики: коэффициент формы

k ф , коэффициент амплитуды

k а ,

коэффициент искажения k и

и коэффициент гармоник

k г .

Коэффициент формы определяется как отношение действующего значения к среднему по модулю значению, например, для силы тока:

k = I

. (4.15)

ср

Коэффициент амплитуды равен отношению максимального значения величины к ее действующему значению:

k = I max . (4.16)

а I

Коэффициент искажения определяется как отношение действующего значения основной гармоники к действующему значению всей величины:

k = I1 . (4.17)

и I

Коэффициент гармоник равен отношению действующего значения высших гармоник к действующему значению основной гармоники:

k = k = 2 . (4.18)

г I

Примечание – Для синусоидальных токов вышеуказанные характеристики

равны: k ф = p (2 2 )» 1.11, k а = » 1.41, k и = 1 и k г = 0 .

4.5 Примеры разложения периодических величин в ряд Фурье и основные свойства периодических кривых, обладающих симметрией

Коэффициенты ряда Фурье (4.4) для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Примеры разложений наиболее распространенных в электротехнике, электронике и автоматике периодических кривых представлены в таблице 4.1.

Таблица 4.1 – Разложения периодических кривых в ряд Фурье

График периодической кривой	Формула разложения
	s(t ) = A m sin w t
	s(t ) = 2 A m T (sin wt sin w t + p 2 t + 1 si n 3wt si n 3w t+ 1 si n 5wt si n 5w t +K⎞ 32 52 ⎟ ⎠
	s(t ) = 8A m ⎛ sin w t - 1 sin 3w t + p 2 ⎜ 32 ⎝ + 1 si n 5w t -K⎞ 52 ⎟ ⎠
	s(t ) = 4 A m ⎛ sin w t + 1 sin 3w t + p ⎜ 3 ⎝ + 1 si n 5w t +K⎞ 5 ⎟ ⎠

На рисунке 4.2 на примере прямоугольного колебания показано его представление частичными суммами ряда Фурье, содержащими одну (рисунок 4.2, а), три (рисунок 4.2, б) и пять (рисунок 4.2, в) гармоник.

а) б) в)

Рисунок 4.2 – Представление прямоугольного колебания частичными суммами ряда Фурье, содержащими одну (а), три (б), и пять (в) гармоник

В случае кривых токов, напряжений и ЭДС, обладающих симметрией, задача представления их рядами Фурье существенно упрощается, поскольку из разложений таких кривых могут выпадать целые спектры гармоник. Рассмотрим простейшие случаи симметрии.

4.5.1 Симметрия относительно оси абсцисс

При таком типе симметрии выполняется условие

s(t ) = -s⎛ t + T ⎞ , (4.19)

⎜ ⎟

⎝ ⎠

то есть отрицательная полуволна является зеркальным изображением сдвинутой на половину периода положительной полуволны. Например, кривая трапецевидной формы (рисунок 4.3) обладает симметрией относительно оси абсцисс.

Рисунок 4.3 – Пример периодической кривой с симметрией относительно оси абсцисс

Ряд Фурье для таких функций не содержит постоянной составляющей и четных гармоник:

A0 = B2 = C2 = K= B2k

= C2k

=K= 0

s(t ) =å(B2k +1 si n(2k + 1)w t + C2k +1 cos(2k + 1)w t ). (4.20)

k =0

4.5.2 Симметрия относительно оси ординат

Этот тип симметрии удовлетворяет условию

s(t ) = s(- t ). (4.21)

Например, колебание треугольной формы (рисунок 4.4) обладает указанным типом симметрии.

Рисунок 4.4 – Пример периодической кривой с симметрией относительно оси ординат

Ряд Фурье для функций с симметрией относительно оси ординат не содержит синусных составляющих, то есть

B1 = B2 =K= B k

=K= 0

s(t ) = A0 +åC k cos k w t . (4.22)

k =1

4.5.3 Симметрия относительно начала координат

Такой тип симметрии наблюдается при условии

s(t ) = -s(- t ). (4.23)

Например, прямоугольное колебание (рисунок 4.5) обладает симметрией относительно начала координат.

Рисунок 4.5 – Пример периодической кривой с симметрией относительно начала координат

В этом случае ряд Фурье не содержит постоянной составляющей и косинусных составляющих, то есть

и, следовательно,

A0 = C1 = C2 =K= C k =K= 0

s(t ) =åB k si n k w t . (4.24)

k =1

4.6 Комплексная форма ряда Фурье. Понятие о дискретных спектрах периодических кривых токов, напряжений или ЭДС

Тригонометрическая форма ряда Фурье может быть преобразована в комплексную следующим образом. Исходя из того, что

sin k w t = 1

j(e- jk w t - e jk w t ),

cos k w t = 1 (e- jk w t + e jk w t ),

выражение, заключенное в скобки в формуле (4.3) преобразуем к виду

B k sin k w t + C k

cos k w t = 1 [(C +

2 k

jB k

)e- jk w t + (C -

jB k

)e jk w t ].

Из формулы (4.4) для коэффициентов B k

и C k

имеем

C k +

jB k

= 2 s(t )e jk w t dt ,

(T )

C k -

jB k

= 2 s(t )e- jk w t dt .

(T )

Следовательно,

¥ ¥ ¥

k =1

(B k

sin k w t + C k

cos k w t ) =

å 1 e- jk w t k =1

(T )

s(t )e jk w t dt +

å 1 e jk w t k =1

(T )

s(t )e- jk w t dt =

-1 ¥

=å 1 e jk w t òs(t )e- jk w t dt +å 1 e jk w t òs(t )e- jk w t dt .

Учитывая, что

k =-¥

(T )

k =1

(T )

1 ⎡ 1 ⎤

A = òs(t )dt = ⎢ e jk w t òs(t )e- jk w t dt⎥ ,

0 T

(T )

⎢T

⎣ (T )

⎥

⎦k =0

ряд Фурье (4.3) представим в виде

+¥

s(t ) = 1 åS k ( jk w )e jk w t , (4.25)

k =-¥

S k ( jk w ) = òs(t )e- jk w t dt . (4.26)

(T )

Соотношение (4.25) для функции s(t ) представляет собой ряд Фурье в

комплексной форме. В этом выражении каждой k - й гармонике отвечает сумма двух

сопряженных членов (при k < 0 и k > 0 ), равная удвоенной вещественной части каждого из этих слагаемых:

1 e jk w t S T k

( jk w )+ 1 e- jk w t S (-

T k

jk w ) = Re⎧ 2 e jk w t S

⎨T

⎩ k

( jk w )⎫ .

⎬

⎭

Обозначив

S k ( jk w ) = S k

(k w )e j a k , имеем

⎨T

Re⎧ 2 S

⎩ k

( jk w )e jk w t ⎫ =

⎬

⎭

2 (k w )cos(k w t + a ) =

T k k

2 (k w )sin(k w t +y ),

T k k

где y k = a k + p 2 .

Таким образом, величина

2 (k w )e j y k =

T k

j T Sk

(k w )e j a k =

j T Sk

( jk w )

представляет собой комплексную амплитуду k - й гармоники:

где

A&km

= A km

e j y k , (4.27)

A = 1 S , A = 2 S

( jk w ) . (4.28)

0 T 0 km T k

Совокупность комплексных амплитуд всех гармоник данной функции является дискретным спектром этой функции. Его можно представить на графике в виде спектра значений амплитуд и спектра значений фаз. По оси абсцисс в таком случае откладывают частоту, которая имеет дискретные значения, равные частотам гармоник. Затем для каждой частоты по оси абсцисс изображают отрезки, параллельные оси

ординат и по длине равные амплитудам

A km

или начальным фазам y k

гармоник. При

этом

A km > 0 , а y k

может быть как положительной, так и отрицательной. Такие

характеристики называются дискретными спектрами или дискретными частотными характеристиками — соответственно, амплитудно-частотной (АЧХ) и фазо- частотной (ФЧХ) характеристиками.

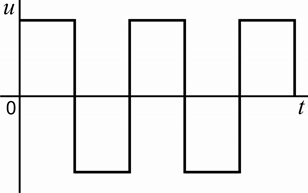
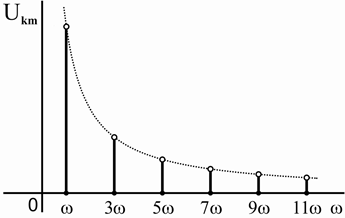
На рисунке 4.6, а изображена временная диаграмма прямоугольного напряжения

u(t ), АЧХ которого представлена на рисунке 4.6, б. Ряд Фурье для прямоугольного

напряжения имеет вид (см. таблицу 4.1):

⎝

⎠

u(t ) = 4U m ⎛ si n w t + 1 si n 3w t + 1 si n 5w t +K⎞ . (4.29)

p ⎜ 3 5 ⎟

а) б)

Рисунок 4.6 – Временная диаграмма прямоугольного напряжения (а)

и соответствующая АЧХ (б)

4.7 Несинусоидальный ток и напряжение в пассивных элементах цепи. Основные закономерности

Рассмотрим некоторые особенности протекания периодических несинусоидальных токов в пассивных элементах цепи, полагая, что периодическое напряжение на зажимах элемента представлено рядом Фурье:

u = U0 +åU km si n(k w t +y uk ). (4.30)

k =1

Коэффициент искажения кривой напряжения тогда равен:

k иu = 1

. (4.31)

4.7.1 Несинусоидальный ток и напряжение в резистивном элементе

Ток и напряжение в резистивном элементе с сопротивлением R (рисунок 4.7, а) связаны законом Ома вида

i(t ) = u(t ) . (4.32)

а) б)

Рисунок 4.7 – Резистивный элемент (а) и соответствующая временная диаграмма тока и напряжения (б)

При периодическом несинусоидальном напряжении (4.30) сила тока согласно

(4.32) равна

где

i = I0 +åI km si n(k w t +y ik ), (4.33)

k =1

I = U0 ,

0 R

I km

= U km ,

y ik =y uk

. (4.34)

Коэффициент кривой тока (4.33), (4.34) равен

k иi = 1

= U1

. (4.35)

Сравнение (4.31) и (4.35) показывает, что

k иi = k иu , т.е. на резистивном элементе

не наблюдается искажения кривой тока в сравнении с кривой напряжением, так что ток и напряжение совпадают по форме и подобны друг другу. На рисунке 4.7, б для прямоугольного напряжения (4.29) с точностью до трех гармоник изображены кривые тока и напряжения.

4.7.2 Несинусоидальный ток и напряжение в индуктивном элементе

Ток и напряжение в индуктивном элементе с индуктивностью L (рисунок 4.8, а) связаны законом Ома вида

i(t ) = 1 u(t )dt . (4.36)

а) б)

Рисунок 4.8 – Индуктивный элемент (а) и соответствующая временная диаграмма тока и напряжения (б)

При периодическом несинусоидальном напряжении (4.30) сила тока согласно

(4.36) равна

где

i =åI km si n(k w t +y ik ), (4.37)

k =1

I km

= U km ,

k w L

y ik

=y uk

- p . (4.38)

Коэффициент кривой тока (4.37), (4.38) равен

k иi = 1 = 1

. (4.39)

Сравнение (4.31) и (4.39) показывает, что

k иi > k иu , т.е. кривая напряжения

искажена больше, чем кривая тока, следовательно, катушка индуктивности является сглаживающим элементом для тока. На рисунке 4.8, б для прямоугольного напряжения (4.29) с точностью до трех гармоник изображены кривые тока и напряжения.

4.7.3 Несинусоидальный ток и напряжение в ёмкостном элементе

Ток и напряжение в ёмкостном элементе с ёмкостью C (рисунок 4.9, а) связаны законом Ома вида

i(t ) = C du(t ) . (4.40)

а) б)

Рисунок 4.9 – Ёмкостной элемент (а) и соответствующая временная диаграмма тока и напряжения (б)

При периодическом несинусоидальном напряжении (4.30) сила тока согласно

(4.40) равна

где

i =åI km si n(k w t +y ik ), (4.41)

k =1

I km

= (k w C )U km ,

y ik

=y uk

+ p . (4.42)

Коэффициент кривой тока (4.41), (4.42) равен

k иi = 1 = 1

. (4.43)

Сравнение (4.31) и (4.43) показывает, что

k иi < k иu , т.е. кривая тока искажена

больше, чем кривая напряжения, следовательно, конденсатор, является сглаживающим элементом для напряжения. На рисунке 4.9, б для прямоугольного напряжения (4.29) с точностью до трех гармоник изображены кривые тока и напряжения.

4.8 Методика расчета линейных электрических цепей при периодических несинусоидальных токах и напряжениях

Возможность разложения периодических несинусоидальных величин, т.е. токов, напряжений и ЭДС, в ряд Фурье позволяет свести расчет линейных электрических цепей при воздействии несинусоидальных ЭДС или токов источников к расчету цепей с постоянными и синусоидальными токами в отдельности для каждой гармоники. Мгновенные значения искомых токов и напряжений в таком случае определяются на основе принципа наложения путем суммирования найденных при расчете постоянных и гармонических составляющих тока или напряжения.

Пусть требуется определить ток в электрической цепи, к которой подключается периодическая несинусоидальная ЭДС:

e(t ) = E0 +åE km si n(k w t +y ek ). (4.44)

k =1

Если цепь линейная, т.е. величины R , L и C неизменны, то ток в цепи определится методом наложения путем суммирования токов, создаваемых каждой из составляющих ЭДС в отдельности:

где

i(t ) = I0 +åI km si n(k w t +y ik ), (4.45)

k =1

I = E0 ,

I = E km ,

y ik

=y uk

- j k

. (4.46)

Здесь Z0 полное сопротивление цепи при нулевой частоте , т.е. сопротивление

постоянному току, Z k — полное сопротивление при частоте k w , угол j k

равен

арктангенсу отношения реактивной составляющей сопротивления Z k

его активной составляющей.

на частоте k w к

В случае цепи с последовательным соединением элементов R , L и C указанные величины, к примеру, равны:

Z k =

, j k

= arctg .

При этом сопротивление

Z0 = ¥ , так как последовательная цепь, содержащая

конденсатор, постоянный ток не пропускает.

Соотношения (4.44) – (4.46) могут быть представлены в комплексной форме:

где

e(t ) = E0

+ Im

k =1

E&km

e jk w t ,

i(t ) = I0

+ Im

k =1

I&km

e jk w t , (4.47)

E&km

= E km

e j y _ek ,

I&km

= I km

e j y ik . (4.48)

Из формул (4.47), (4.48) следует, что расчет периодических несинусоидальных токов, представленных в комплексной форме, сводится к определению комплексных

амплитуд токов

I&km , соответствующих комплексным амплитудам ЭДС

E&km , для

различных порядков гармоник k . При этом комплексное сопротивление для данной

частоты k w (для данной гармоники) определяется выражением

Z = Z e j j k . (4.49)

Рассмотрим, к примеру, электрическую цепь, изображенную на рисунке 4.10, и определим для нее ток i(t ) в ветви с источником ЭДС.

Рисунок 4.10 – Схема, иллюстрирующая применение метода наложения к расчету линейных цепей при периодических несинусоидальных ЭДС и токах

Так как при расчете спектр рассматриваемых гармонических составляющих всегда ограничивается, то вместо ряда (4.44) следует рассматривать его n - ю частичную сумму, т.е. функцию

e(t ) =åE km si n(k w t +y ek ). (4.50)

k =0

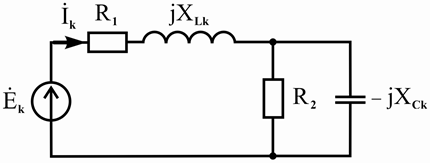
Для определения искомого тока i(t ) исходную схему рисунка 4.10 представим

расчетными схемами, изображенными на рисунке 4.11. При этом на рисунке 4.11, а изображена расчетная схема, соответствующая постоянной составляющей или нулевой

гармонике E0 ; на рисунке 4.11, б — расчетная схема, соответствующая гармоническим

составляющим

E km sin(k w t +y ek ),

k = 1,n .

а) б)

Рисунок 4.11 – Расчетные схемы для постоянной (а) и гармонических (б) составляющих периодической несинусоидальной ЭДС

Величины

X Lk

= k w L и

X Ck

= 1 (k w C )

на рисунке 4.11, б определяют

соответственно реактивные сопротивления катушки и конденсатора для k - й

гармоники,

E&km и

I&km

— комплексные амплитуды ЭДС и тока (аналогично

соотношениям (4.48)).

Для схемы замещения на рисунке 4.11, а относительно постоянной составляющей тока находим

I0 =

E 0

R1 + R2

. (4.51)

Для схемы замещения на рисунке 4.11, б относительно гармонических составляющих тока:

I& = E&km , (4.52)

km Z

где полное комплексное сопротивление Z k цепи для k - й гармоники ЭДС равно:

Z = R + jX

+ R2 (-

jX Ck ) . (4.53)

k 1 Lk

R2 -

jX Ck

вида

На основании (4.51) – (4.53) искомый ток i(t ) изобразится n - й частичной суммой

i(t ) = I0 +åI km si n(k w t +y ik ), (4.54)

k =1

где амплитуда

I km

k - й гармоники равна модулю комплексной амплитуды (4.52), а

начальная фаза y ik

— ее аргументу:

I km =

I&km ,

y ik

= arg I&km . (4.55)

Соотношения (4.51) – (4.55) дают полное решение поставленной задачи, т.е.

позволяют с точностью до n гармоник рассчитать мгновенное значение тока i(t ) в

неразветвленной части цепи, изображенной на рисунке 4.10, при воздействии на нее периодической ЭДС (4.50). Обобщая эти результаты, можно сформулировать алгоритм расчета произвольной электрической цепи при периодических несинусоидальных ЭДС и токах.

Порядок расчета электрической цепи при периодических несинусоидальных ЭДС и токах

1) Произвести разложение периодических несинусоидальных ЭДС и токов источников на гармонические составляющие, т.е. в виде соответствующих рядов Фурье (4.6).

2) Выполнить расчет цепи методами анализа цепей постоянного и переменного синусоидального токов для каждой из составляющих в отдельности.

3) Определить искомые величины в соответствии с принципом наложения как алгебраические суммы найденных гармоник.

Примечания

1 Необходимо помнить, что из-за различных частот суммировать комплексы различных гармоник недопустимо.

2 При расчете токов и напряжений, возникающих от действия постоянной составляющей ЭДС или тока источника, следует учитывать, что индуктивная катушка не оказывает противодействия постоянному току (эквивалентна короткому замыканию), а конденсатор, наоборот, является для постоянного тока бесконечно большим сопротивлением (обрывом). Это означает, что при составлении схемы замещения относительно постоянных составляющих токов и напряжений (см., например, схему рисунка 4.11, а) все индуктивные элементы следует исключить из схемы, закоротив их, а все ветви с ёмкостными элементами разомкнуть.

4.9 Мощность периодического несинусоидального тока

Выражение мгновенной мощности

p(t ) = i(t )u(t )

(4.56)

справедливо для токов и напряжений с любой формой кривой. Активная мощность периодического тока произвольной формы определяется как среднее значение его мгновенной мощности за период:

T T

P = 1 ò p(t )dt = 1 òi(t )u(t )dt . (4.57)

T T

0 0

Используя представление негармонического тока Фурье (4.6), т.е. выражениями

i(t )

и напряжения

u(t )

рядами

i = I0 +åI km si n(k w t +y ik ),

k =1

u = U0 +åU km si n(k w t +y uk ),

k =1

мгновенную мощность (4.56) запишем следующим образом:

¥ ¥

p(t ) = I0U0 +åI0U km si n(k w t +y uk )+åU0I km si n(k w t +y ik )+

k =1

+ åI km U km si n(k w t +y ik )si n(k w t +y uk )+

k =1

¥ ¥

+ ååI km U nm si n(k w t +y ik )si n(n w t +y un ). (4.58)

k =1

n=1 k ¹n

Подставляя соотношение (4.58) в формулу (4.57), после несложных преобразований получим

где j k

=y uk -y ik

P = I0U0 +åI k U k cos j k , (4.59)

k =1

— угол сдвига фаз между напряжением и током k - й гармоники. Из

(4.59) следует, что активная мощность периодического несинусоидального тока равна сумме активных мощностей всех гармонических составляющих и мощности постоянных составляющих тока и напряжения:

P = P0 +åP k ,

k =1

P0 = I0U0 ,

P k = I k U k cos j k . (4.60)

Аналогично (4.59) для реактивной мощности можно записать:

Q =åQ k =åI k U k si n j k . (4.61)

k =1 k =1

Полная мощность несинусоидального тока соответственно определится выражением

S = IU =

. (4.62)

Отношение активной мощности к полной называют коэффициентом мощности и приравнивают к косинусу некоторого условного угла q :

cos q = P =

I0U0 +åI k U k cos j k

k =1

. (4.63)

Заметим, что для несинусоидальных токов (в отличие от синусоидальных) не выполняются соотношения треугольника мощностей, т.е. в общем случае квадрат полной мощности не равен сумме квадратов активной и реактивной мощностей, поэтому

Величина

S ¹ .

T = S 2 - (P2 + Q2 )

(4.64)

называется мощностью искажения. Мощность искажения определяется произведениями действующих значений разнопорядковых гармоник тока и напряжения

и характеризует степень различия в формах кривых тока i(t ) и напряжения u(t ). В

частности, если сопротивление цепи активное, то кривые тока и напряжения подобны и при этом Q = 0 и T = 0 .

Дата добавления: 2019-07-15; просмотров: 433; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Мы поможем в написании ваших работ!