Лекция 6. Переходные процессы в линейных электрических цепях и методы их анализа 2 страница
системы уравнений получить одно дифференциальное уравнение, содержащее только основную переменную;
3) записать общее решение дифференциального уравнения в виде (6.8), т.е. как
сумму свободной и принужденной составляющих x св (t ) и x пр (t );
4) определить принужденную составляющую x пр (t ) методами расчета цепей в установившемся режиме;
5) составить характеристическое уравнение (6.10) и определить его корни l k ;
6) составить выражение для свободной составляющей x св (t ) согласно формуле (6.11) и таблице 6.1;
7) записать начальные условия; если условия ненулевые, то определить токи в индуктивностях и напряжения на ёмкостях методами расчета цепей в установившемся режиме при t = 0- ;
8) определить постоянные интегрирования A m и c m ;
9) подставить полученные значения A m , c m , x пр (t ) и l k в общее решение
x(t ) = x св (t )+ x пр (t ), провести анализ полученного решения и построить графики изменения искомой величины.
Далее (в разделах 6.7 – 6.9) рассмотрены примеры анализа переходных процессов
в электрических цепях. Они имеют самостоятельное значение и иллюстрируют суть классического метода.
6.7 Переходные процессы в цепях с индуктивной катушкой
Рассмотрим переходные процессы в цепи, состоящей из последовательно включенных участков с сопротивлением R и индуктивностью L (переходные процессы в реальной катушке индуктивности).
6.7.1 Включение индуктивной катушки на постоянное напряжение
|
|
|
Исследуем переходной процесс, возникающий при подключении R , L – цепи
(индуктивной катушки) к источнику постоянной ЭДС E = const (рисунок 6.2, а).
 |  |
а) б)
Рисунок 6.2 – Схема замещения цепи (а) и временная диаграмма токов и напряжений в индуктивной катушке (б) при подключении к источнику постоянного напряжения
В послекоммутационном режиме, когда ключ K замкнут, переходной процесс в цепи описывается дифференциальным уравнением
L di + Ri = E . (6.12)
dt
Соответствующее однородное уравнение, определяющее свободный ток i св , будет
Его характеристическое уравнение
L di св
dt
+ Ri св
= 0 . (6.13)
имеет единственный корень l = - R
L l + R = 0
L , поэтому
(6.14)
i св
= Ae l t = Ae
- R t L
- t
= Ae t , (6.15)
где величина t = L R называется постоянной времени: [ ] = 1с (секунда).
Ток установившегося режима
i пр
= E . (6.16)
R
Переходной процесс в цепи определяется суммой свободной и принужденной составляющих, поэтому из (6.15) и (6.16) следует:
|
|
|
- t
i = i св + i пр = Ae t
+ E . (6.17)
R
Для определения постоянной интегрирования A воспользуемся 1-м законом
коммутации. До коммутации ток в индуктивной катушке был равен нулю ( i L (0- ) = 0 ),
следовательно, в первый момент времени после коммутации ток i L (0+ ) = i(0+ ) будет также равен нулю:
i L (0-
) = i L
(0+
) = i(0+
) = A + E = 0 .
R
Отсюда
A = - E
R , поэтому выражение (6.17) можно представить в виде
⎛
E
i = ⎜1 - e R ⎝
- t ⎞
t ⎟ ,
⎠
t = L
R
, (6.18)
т.е. ток в цепи нарастает до установившегося значения (6.16) по экспоненциальному закону с постоянной времени , которая определяет скорость этого процесса.
Напряжение на резистивном элементе с сопротивлением R пропорционально току (6.18):
⎛
u R = Ri = E⎜1 - e
⎝
- t ⎞
t ⎟ . (6.19)
⎠
Напряжение на индуктивном элементе с индуктивностью L :
di
=
u L L dt
- t
= Ee t . (6.20)
Графики изменения величин i , u R
и u L
в переходном процессе, построенные
|
|
|
согласно формулам (6.18) – (6.20), приведены на рисунке 6.2, б. В первый момент времени после коммутации напряжение на индуктивном элементе скачком возрастает до
значения u L (0+ ) = E , после чего по экспоненциальному закону уменьшается до нуля.
Примечание – Постоянная времени численно равна промежутку времени, за
который экспоненциально изменяющаяся величина убывает в e » 2,72 раза. Чем
больше , тем медленнее затухает экспоненциальная функция и тем дольше длится переходной процесс в цепи. Теоретически переходной процесс длится бесконечно долго, однако практически его можно считать завершенным по истечении времени
t = (3 ¸ 5)t .
6.7.2 Отключение индуктивной катушки от источника постоянного напряжения
Исследуем переходной процесс, возникающий при отключении R , L – цепи
(индуктивной катушки) от источника постоянного напряжения и подключении ее к
ветви с активным сопротивлением R0
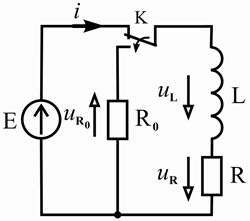
(рисунок 6.3, а).
После коммутации электрическое состояние цепи определяется уравнением
L di + (R + R
)i = 0 . (6.21)
|
|
|
dt 0
Отсутствие правой части в этом уравнении означает, что переходной ток равен
свободному, а установившийся — нулю:
i = i св ,
i пр = 0 . Характеристическое уравнение
для (6.21) аналогично (6.14), поэтому решением уравнения (6.21) является
выражение (6.15)
- t
i = i св = Ae t ,
в котором постоянная времени
t = L
(R + R0 ). Поскольку до коммутации ток в цепи
определялся напряжением источника и сопротивлением катушки, т.е.
i(0-
) = E ,
R
то A = E
R и выражение для переходного тока имеет вид
i = E
R
- t
e t ,
t = L
R + R0
. (6.22)
а) б)
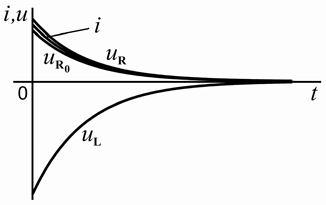
Рисунок 6.3 – Схема замещения цепи (а) и временная диаграмма токов и напряжений в индуктивной катушке (б) при отключении от источника постоянного напряжения
Напряжения на резистивном и индуктивном элементах равны:
- t
R - t
di R + R
- t
u R = Ri = Ee t ,
u = R0i = 0 Ee t ,
|
u L = L dt
= - 0 Ee t . (6.23)
R
|
и u L
в переходном процессе, построенные
согласно формулам (6.22), (6.23), приведены на рисунке 6.3, б.
Примечание – Если резистор R0
имеет большее сопротивление, чем индуктивная
катушка, то напряжение на нем в начальный момент времени после коммутации будет
больше приложенного напряжения (больше ЭДС источника E ). Так, если
( n > 1), то напряжение на резисторе
R0 = nR
u (0 ) = R0 E = nR E = nE .
R0 + R R
Это обстоятельство следует иметь в виду при размыкании цепей, содержащих индуктивные элементы, так как при этом могут возникать перенапряжения, в частности,
при отсутствии в цепи резистора
R0 , включенного параллельно индуктивной катушке,
отключение ее от источника может сопровождаться возникновением между размыкающими контактами дугового разряда.
6.7.3 Короткое замыкание индуктивной катушки в цепи постоянного тока
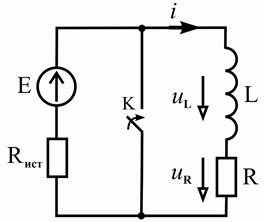
Исследуем переходной процесс, возникающий при коротком замыкании R , L – цепи (индуктивной катушки), подключенной к источнику постоянного напряжения (рисунок 6.4, а).
а) б)
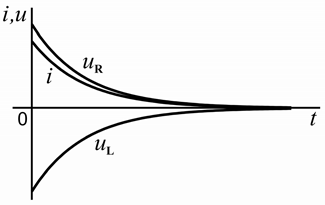
Рисунок 6.4 – Схема замещения цепи (а) и временная диаграмма токов и напряжений в индуктивной катушке (б) при коротком замыкании
Запишем дифференциальное уравнение переходного процесса в цепи после замыкания ключа:
L di + Ri = 0 . (6.24)
dt
Так как дифференциальное уравнение (6.24) однородное, т.е. совпадает с уравнением (6.13), то его общее решение содержит только свободную составляющую:
- t
i = i св = Ae t ,
где постоянная времени t = L R . Поскольку в докоммутационном режиме через
индуктивную катушку протекал постоянный ток
i(0- ) =
E ,
R + R ист
где R ист
— внутренне сопротивление источника ЭДС, то постоянная интегрирования
A = E
(R + R ист ) и выражение для переходного тока
i = E
R + R ист
- t
e t ,
t = L
R
. (6.25)
Напряжения на резистивном и индуктивном элементах равны:
u R = Ri =
R
R + R ист
- t
Ee t ,
di
|
= - R
R + R ист
- t
Ee t . (6.26)
Графики изменения величин i , u R
и u L
в переходном процессе, построенные
согласно формулам (6.25), (6.26), приведены на рисунке 6.4, б.
6.7.4 Включение индуктивной катушки на синусоидальное напряжение
Исследуем переходной процесс, возникающий при подключении R , L – цепи
(индуктивной катушки) к источнику синусоидальной ЭДС (рисунок 6.5, а):
e = E m sin(w t +y e ),
где E m , и y e — амплитуда, угловая частота и начальная фаза этой ЭДС. Так как
начало отсчета времени совпадает с моментом коммутации, то величина y e зависит от
момента включения синусоидального источника в R , L – цепь и называется поэтому
фазой включения.
 |  |
а) б)
Рисунок 6.5 – Схема замещения цепи (а) и временная диаграмма токов и напряжений
в индуктивной катушке (б) при подключении к источнику синусоидального напряжения
Дифференциальное уравнение для рассматриваемой цепи имеет вид
L di + Ri = e . (6.27)
dt
где
Установившийся ток
i пр = I m sin(w t +y e - j ), (6.28)
I m =
E m ,
j = arctg
X L ,
R
X L = w L . (6.29)
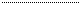Уравнение для свободного тока
i св
и его общее решение сохраняют тот же вид
(6.13), (6.15), что и для цепи с источником постоянного напряжения:
- t
i = i св = Ae t ,
где постоянная времени t = L R . На основании (6.28) и (6.29) получаем тогда
Дата добавления: 2019-07-15; просмотров: 168; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!