Лекция 3. Электрические цепи однофазного синусоидального тока 8 страница

где проводимости g , b L

и b C

при заданных значениях параметров R , L и C

определяются согласно формулам (3.32), (3.41) и (3.50).

Режим работы участка цепи с параллельными ветвями, при котором сдвиг фаз между напряжением на его выводах и общим током равен нулю, называется резонансом токов. Условием возникновения резонанса токов является равенство реактивных проводимостей индуктивной катушки и конденсатора:

b = b , 1 = w C , (3.113)

L C 0

где частота w0 , при которой наблюдается резонанс напряжений, называется резонансной частотой параллельного контура. Из сравнения условий (3.113) резонанса токов с аналогичными условиями (3.108) резонанса напряжений следует, что математически

указанные соотношения эквивалентны, поэтому значения угловой частоты w0 ,

индуктивности L0

и ёмкости

C0 , при которых наступает резонанс токов, определяются

согласно (3.113) из формул аналогичных равенствам (3.109):

w0 = ,

L0 =

w 2C ,

C0 =

w 2L

. (3.114)

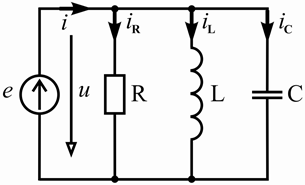
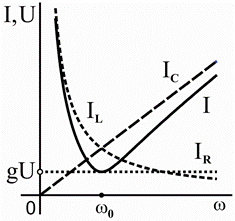
а) б)

Рисунок 3.24 – Параллельный колебательный контур (а) и резонансные кривые токов и напряжений (б)

Соотношения (3.114) показывают, что резонанс токов (как и резонанс напряжений) может быть достигнут при изменении или частоты приложенного напряжения, или индуктивности катушки, или ёмкости конденсатора.

Если напряжение U и активное сопротивление R цепи не изменяются, то

согласно (3.112) ток

I0 при резонансе токов, т.е. при реактивной проводимости

b = b L - b C = 0

значения:

и полной проводимости

Y = g , достигает своего наименьшего

I0 = I min = Ug .

Индуктивная и ёмкостная проводимость при резонансе

w C = 1 =

= g . (3.115)

Величина называется характеристической (или волновой) проводимостью цепи или контура. Отношение величины тока в индуктивности или ёмкости при резонансе к величине тока в источнике называется добротностью контура или

коэффициентом резонанса:

q = I L (w0 ) = I C (w0 ) = U = w0CU = g

. (3.116)

I0 I0 w0LgU gU g

Как и ранее (см. раздел 3.12.1), величина

затуханием контура.

d = 1 q , обратная добротности, является

Добротность показывает, во сколько раз токи в реактивных элементах контура превышают ток источника при резонансной частоте.

В высокодобротных контурах, т.е. при

q >> 1

( d << 1), токи в реактивных

элементах (индуктивных катушках и конденсаторах) в режиме резонанса могут превосходить, и иногда весьма значительно, суммарный ток в цепи. Действительно, при

резонансе токов, когда b L = b C , токи в индуктивных катушках и конденсаторах также

равны: I L (w0 ) = I C (w0 ). Поэтому, если при резонансе увеличить в одинаковое число раз

n ( n > 1) индуктивную и ёмкостную проводимости, т.е. выбрать b * (w ) = nb (w ) и

L 0

b * (w ) = nb (w ), то общий ток в цепи не изменится, а токи в индуктивном и ёмкостном

C 0

элементах увеличатся в n раз: I * (w ) = nI (w ) и I * (w ) = nI (w ). По этой причине

L 0 C 0

резонанс в параллельном колебательном контуре и называется резонансом токов.

Зависимости токов и напряжений в колебательном контуре от частоты, т.е.

функции I (w) и U (w ), при неизменных значениях параметров R , L и C называются

частотными характеристиками, а их графические изображения — резонансными

кривыми. На рисунке 3.24, б изображены резонансные кривые

I C (w ) для параллельного колебательного контура.

I (w),

U (w ),

I L (w ) и

Примечание – Резонанс токов в отличие от резонанса напряжений — явление безопасное для энергетических установок. Резонанс токов, как и резонанс напряжений, находит применение в радиотехнических устройствах.

3.12.3 Резонанс токов в параллельном колебательном контуре с потерями. Основные закономерности

Рассмотрим параллельный колебательный контур, в ветвях которого кроме реактивных элементов, т.е. индуктивностей L и ёмкостей C , содержатся активные

сопротивления R L и R C , учитывающие потери в элементах контура (рисунок 3.25, а).

а) б)

Рисунок 3.25 – Параллельный колебательный контур с потерями (а) и векторная диаграмма токов и напряжений в режиме резонанса (б)

При величине действующего напряжения источника U действующее значение тока I в контуре может быть рассчитано согласно закону Ома (3.112), в котором

проводимости g , b L

и b C

при заданных значениях параметров

R L , L , R C и C

определяются согласно следующим формулам:

g = g L

+ g C ,

g L =

R L

R2 + (w L)2 ,

g C =

R C

R2 + (1 w C )2

, (3.117)

b = wL ,

L R2 + (w L)2

b = 1 wC . (3.118)

C R2 + (1 w C )2

Условием возникновения резонанса токов в параллельном колебательном контуре с потерями, как и в ранее рассмотренном параллельном контуре на рисунке 3.24, а, является равенство реактивных проводимостей ветвей контура:

или, учитывая (3.118),

b L = b C

(3.119)

wL = 1 wC . (3.120)

R2 + (w L)2 R2 + (1 w C )2

Из уравнения (3.120) следует, что условие резонанса токов в параллельном контуре с потерями определяется значениями не только реактивных, но и активных

сопротивлений ветвей R L и R C . Кроме того, из формулы (3.120) следует, что

изменением одной из величин ,

R L , L , R C

и C при фиксированных значениях

остальных четырех не всегда может быть достигнут резонанс.

Резонанс отсутствует, когда значение изменяемой величины при ее определении из уравнения (3.120) получается комплексным. Для параметров L , C могут получаться и по два различных вещественных значения, удовлетворяющих уравнению (3.120). В таких случаях изменением L и C можно достичь двух различных резонансных режимов.

Решая уравнение (3.120) относительно , найдем следующее значение для резонансной угловой частоты:

w р = w0

, (3.121)

где w0

— частота, определяемая из (3.114), — волновое сопротивление (3.110).

Для получения резонанса сопротивления R L и R C должны быть оба больше или

оба меньше . Если это условие не выполняется, то получается мнимая частота w р , т.е. не существует такой частоты, при которой имел бы место резонанс.

При R L = R C ¹ r резонансная частота w р = w0 , т.е. такая же, как и при резонансе

в последовательном контуре.

При R L = R C = r резонансная частота

w р = 0 0

имеет любое значение, т.е.

резонанс наблюдается на любой частоте.

Если напряжение U и активные сопротивления

R L и R C

ветвей контура не

изменяются, то согласно (3.119) ток I0

при резонансе токов в контуре с потерями, т.е.

при реактивной проводимости

b = b L - b C = 0

и полной проводимости

Y = g ,

достигает своего наименьшего значения:

I0 = I min = Ug ,

где полная активная проводимость g контура определяется из формул (3.117). Векторная диаграмма токов и напряжений в режиме резонанса приведена на рисунке 3.25, б.

Примечание – В радиотехнике и электросвязи применяются контуры с малыми

потерями, т.е. в них R L << r и R C << r . Это означает, что для таких контуров

резонансная частота

w р , как следует из (3.121), практически совпадает с резонансной

частотой w0 параллельного контура, изображенного на рисунке 3.24, а: w р » w0 .

3.13 Комплексный метод расчета цепей синусоидального тока

Уравнения (3.70), (3.72), выражающие законы Кирхгофа в комплексной форме для цепей синусоидального тока, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока:

åI&k

k =1

= 0 ,

åI&k Z k k =1

=åE&k .

k =1

Только токи, напряжения, ЭДС и сопротивления (или проводимости) входят в эти уравнения в виде комплексных величин.

Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называют методом комплексных величин или комплексным методом.

Последовательность расчета цепей синусоидального тока комплексным методом

1) Для исходной схемы цепи составить эквивалентную ей схему замещения относительно комплексов величин, что означает замену ЭДС и токов источников, т.е.

гармонических функций e(t ) и j(t ), их комплексами E& и J& , а параметров R , L и C

пассивных элементов — их комплексными сопротивлениями (или проводимостями)

Z R = R ,

Z L =

jX L

и Z C

= - jX C . Указанные преобразования следует производить

согласно таблице 3.7.

Таблица 3.7 – Основные элементы цепи и комплексные схемы замещения

Тип элемента	Элемент цепи	Исходная схема замещения	Комплексная схема замещения
Активные элементы	Источник ЭДС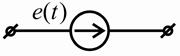
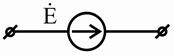
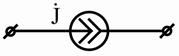
Активные элементы	Источник тока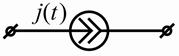
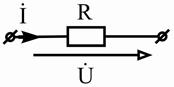
Пассивные элементы	Резистивный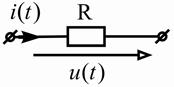
	Индуктивный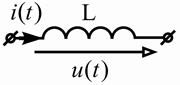
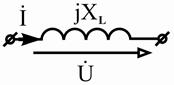
	Ёмкостный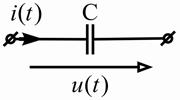

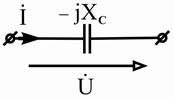
2) Составить полную систему уравнений на основании 1-го и 2-го законов Кирхгофа в комплексной форме.

3) Найти решение системы уравнений относительно комплексов искомых величин, например, комплексов токов I& .

4) Для полученных комплексов искомых величин выполнить переход к функциональному представлению этих величин в форме мгновенных значений,

например, токов i(t ) как гармонических функций времени.

Продемонстрируем применимость метода комплексных величин на примере разветвленной цепи синусоидального тока, изображенной на рисунке 3.26, а.

а) б)

Рисунок 3.26 – Разветвленная цепь синусоидального тока (а) и соответствующая ей схема замещения в комплексном представлении (б)

)

В рассматриваемой цепи действуют два источника энергии: источник тока

Дата добавления: 2019-07-15; просмотров: 138; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!