МЕТОДИКА ИЗУЧЕНИЯ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ

⇐ ПредыдущаяСтр 12 из 16Следующая ⇒

ПРИБАВИТЬ И ВЫЧЕСТЬ 2, 3, 4. ЗНАКОМСТВО С ПЕРЕМЕСТИТЕЛЬНЫМ СВОЙСТВОМ СЛОЖЕНИЯ. ПРИБАВИТЬ 5,6,7,8,9. ОЗНАКОМЛЕНИЕ СО СВЯЗЬЮ МЕЖДУ КОМПОНЕНТАМИ И РЕЗУЛЬТАТОМ ДЕЙСТВИЯ СЛОЖЕНИЯ.

Подготовительная работа: начин-ся с первых уроков. Обр-ся внимание на то, что когда приб-т станочится больше и наоборот. К концу изуч-я нум-ии у. должны прочно усвоить способы образ-я любого числа первого десятка присчит-м и отсчитыв-м любого первого десятка.

На втором этапе рассм-т случаи сложен-я и вычит-я вида а+- 2, а
+- 3, а+- 4.

План работы:

1. Подго-е упраж-я

2. Знакомство с приемами выч-ия

3. Закрепл-е зн-ий приемов., выбраб. Выч-го навыка

4. Состав-е и заучивание таблиц

На подг. Этапе надо научить решать примеры вида 6+1+1; 9-1-1. Затем к рассм-ю приема прибал. И вычита-я 2. Решается пример 4+2. Пусть эти букеты на окне изоб-т число 4, а на столе – число 2. Запишем, что сделала Вова. Ск-ко вышло? Как можно прибавить 2 к 4? Чт-ы это сделать надо сначала прибавить к 4 1, а потом к 5 еще 1. =6.

Далее преход к изучению вычисления а+_3,4. Для приемов а +- 4 м.б. запись такой же, но целесо-но начать запись подругому. 5+4 = 5+2+2.= 9. Далее провод-ся упраднениядля того, чтобы знания стали навыками. Эффек-о также сравнивать м\у собой числа.

Завершающий момент – составление и заучивание таблиц, часть вместе, часть сам-но.

След. этап выячисления с 5,6,7,8,9. Записывают пример 5+4=9, прод-я действия с синими и красн-ми кружками. Для закр-я знаний меж-у суммой и слаг-ми уч-ся вып-ют упр-я по данному прим-ру на слож-е сост-т два примера на выч-ие и реш-ют их, с тремя данными числами. 4,3,7. Сост-т 4 примера, затем прист-т к раскр-ю нового приема выч-я. У. пред-т детям объ-ть, как можно решить пример 10-8. Нах – т более удобный способ. (Вот у нас 10 из расл-х слаг-х, 10 – это 8 и 2, этот пример будет нашим помощ-м. Если из суммы 8 и 2 выч-ть 8, ск-ко ост-ся?

-2, запис-т ответ и показ-ют на кружках.

-Теперь нам надо реш-ть пример 10-6. Какими слаг-ми заменим 10, чтобы выч-ть 6?

- 6 и 4, вычит-м 6,пол-ся 4

Закан-ся работа над «Десятком» повтор-м и закреп-м изуче-го.

Подготовка к усвоению связи между компонентами и результатом действия сложения проводится с самого начала работы над сложением и вычитанием. С этой целью предусматриваются специальные упражнения: по данному рисунку (1 большой мяч и 2 маленьких мяча) составить примеры на сложение и вычитание или же по одному и тому же рисунку составить задачу на сложение и задачу на вычитание; решить и сравнить пары примеров вида: 4+3 н 7-3.

Ознакомлению со связью между компонентами и результатом действия сложения отводится специальный урок. Работу над новым материалом можно провести так.

Учитель предлагает детям проиллюстрировать красными и синими кружками пример на сложение (5+4=9). Пример читают с названием чисел при сложении. Затем предлагают из всех кружков убрать (отодвинуть) красные кружки, выясняют, какие кружки остались и сколько их. Записывают новый пример: 9—5=4 и читают, называя числа так, как они назывались в первом примере (из суммы 9 вычли первое слагаемое, получили второе слагаемое 4).

5 + 4 = 9

----------------

9 - 5 = 4

Аналогично рассматривают пример: 9-4=5.

Подобных упражнений надо выполнить достаточное количество, чтобы на основе своих наблюдений дети смогли сами сделать вывод: если из суммы вычесть первое слагаемое, получится второе слагаемое; если из суммы вычесть второе слагаемое, получится первое слагаемое.

Для закрепления знаний связи между суммой и слагаемыми учащиеся выполняют такие упражнения: по данному при' меру на сложение составляют два примера на вычитание и решают их (2+4=6, 6—4= , 6—2== ), с тремя данными числами (4, 3, 7) составляют и решают четыре примера(4+3,3+4, 7-4, 7-3).

Знание связи между компонентами и результатом действия сложения используется для нахождения результатов вычитания (случаи «вычесть 5, 6, 7, 8, 9»). На уроке, посвященном ознакомлению детей с этим приемом вычитания, прежде всего, повторяют состав чисел 6, 7, 8 и др., а также закрепляют знание изученной взаимосвязи.

5.2. Умножение. Переместительное свойство умножения. Методика изучения зависимости между компонентами и результатом действия умножения.

Переместительное свойство умножения (переместительный закон умножения).

От перестановки мест множителей произведение не изменяется.

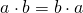С помощью букв переместительное свойство умножения записывают так:

Переместительное свойство умножения позволяет выбирать более удобный способ умножения чисел.

Примеры.

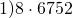
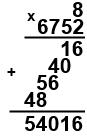
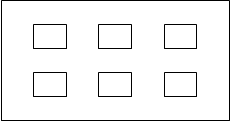Связь между компонентами и результатом действия умножения раскрывается с помощью наглядных пособий.

2·3=6

6:2=3

6:3=2

После выполнения нескольких упражнений ученики делают вывод: если произведение двух чисел разделить на первый множитель, то получим второй множитель, а если произведение двух чисел разделить на второй множитель, то получим первый множитель.

Позднее два вывода объединяют в один: если произведение двух чисел разделить на один из множителей, то получим другой множитель.

На этом же этапе изучаются приёмы для случаев умножения и деления с числами 1 и 10. Раскрывая приёмы, учащиеся будут применять только что полученные знания, а, следовательно, лучше усвоят их. Кроме того, они овладеют рядом приёмов, на основе которых будут быстро находить результаты, отпадает необходимость в заучивании этих результатов.

Сначала рассматривается случай умножения единицы на числа, большие единицы. Учащиеся решают ряд примеров, находят результат сложением: 1· 2=1+1=2.

Затем, сравнив в каждом случае результат с множителями, они приходят к выводу: при умножении единицы на любое число получается то число, на которое умножали. В дальнейшем аналогичные примеры решаются на основании этого правила.

Далее вводится правило умножения на 1: при умножении любого числа на 1 получается то число, которое умножали, например: 4 · 1=4, 12 · 1=12. Здесь невозможно использовать приём замены произведения суммой, на этом же основании нельзя опираться и на перестановку множителей. Поэтому надо просто сообщить детям это правило, и в дальнейшем использовать его в вычислениях.

5.3. Деление. Методика изучения зависимости между компонентами и результатом действия деления.

- Пример: 30:6

- Чем яв-ся чило 30? (делимое)

- Чем яв-ся число 6? (делитель)

- Что нужно найти? (частное)

- Как мы найдем частное? (Делимое делим на делитель и получаем частное).

- Чему будет равно частное? (5)

- Вывод: Для того чтобы найти частное нужно делимое разделить на делитель.

- Пример: 30: =5

- Что неизвестно? (Делитель)

- Как найти неизвестное? (Делимое разделить на частное)

- Чему будет равен делитель? (6)

- Вывод: Для того чтобы найти делитель, нужно делимое разделить на частное

- Пример: :6=5

- Чем яв-ся число 6? (делитель)

- Чем яв-ся число 5? (частное)

- Что нужно найти? (делимое)

- Как найдем? (Делитель умножить на частное)

- Ск-ко получ-ся? (30)

- Вывод: Для того чтобы найти делимое, нужно делитель умножить на частное.

- Общий вывод: Чтобы найти частное, нужно делимое разделить на делитель.

Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Чтобы найти неизвестное делимое нужно делитель умножить на частное.

5.4. Методика изучения таблицы умножения и деления. Приемы заучивания.

Сущ-ют 2 плдхода к изучению таблицы умножения:

1) по постоянному первому множителю: 3⦁3=3+3+3, 3⦁4=3+3+3+3. Преимущества – находим рез-т через сумму равных слагаемых. Недостаток - слаг-х может быть очень много. В этом случае при нах-ии след-го значения выр-ия польз-ся рез-ом предыдущего.

2) по постоянному второму множителю: 5⦁3=5+5+5, 4⦁3=4+4+4. Преимущества – количество слаг-х каждый раз одинаково. Недостаток – слагаемые в каждой строке разные.

На одном уроке детей одн=но знак-ть с четырьмя таблицами: две умножение, две на деление. Но фактически их 5 – еще таблица сложения.

Первая таблица умн-ия составляется на основе конкретного действия умножения, т.е. таблица сложения по-любому постоянному множителю.

Вторая таблица умножения составляется на основе переместительногосв-ва действия умн-ия: чем похожи, чем отлич-ся выр-ия в первой и второй табл. умн-ия, какой можно сделать вывод.

Первая таблица деления составляется на основе зависимости действия умн-ия относительно первой таблицы: чем яв-ся числа 9 и 3 в первой таблице умн-ия (произ-ем и первым множ-ем), если произ-ие разделить на первый мн-ль, то что получим? (второй множитель)

Вторая таблица на деление составляется аналогично первой таблице умножения, но теперь уже относ-но второго множителя.

После составления всех таблиц проводится работа по заучиванию (каждый раз стираются все рез-ты):

1. Вызывают четырех уч-ся, к-ые записывают ответы.

2. Пров-ся рез-ты в разбивку.

3. Записываются примеры на умн-ие и деление: 5⦁6, 6⦁5, 30:5, 30:6

4. Отгадай задуманное число: На какое число я умножила 8 и получила 40? (5)

5. Замени число 36 призв-ем двух чисел

6. Японская машинка.

Итогом всей работы служит сводная таблица для заучивания.

5.5. Методика изучения "Деление с остатком". Применение правил деления с остатком при делении многозначных чисел.

1) Рассм-м конкретный смысл действия деления с остатком. Рассм-ся практически, исп-я задачи на деление по содержанию и на равные части с отатком.

Деление по содержанию: 13 круж-ов разложили в кучку по 4 курж. В каждой. Ск-ко получили кучек с кружочками?

- Делить нужно сразу по 4 кружочка (3 кучки и 1 кружочек остается) 13:4=3 (в ост. 1)

Деление на равные части: 11 палочек нужно раздать 5 уч-ся. По ск-ко палочек пол-т каждый?

- Делить нужно по одной палочке. В рез-те пол-ся по 2 палочки и 1 остается. По ходу делается запись и чтение. 11:5=2 (ост. 1)

На уроке можно исп-ть любой тип деления.

2) Соотношение между делителем и остатком.

Перед уроком на доску щзаписать выр-ия с остатком. Н-р: 2:2=1

3:2=1 (ост 1)

4:2=2

5: 2=2 (ост 1) и т.д.

Рассм-ся каждый столбик в отдельности и сравнивается с остатком с делителем. Делается вывод, что при делении на 2 остаток может быть равен 1, при делении на 2 остаток может быть 1 и 2.

Затем делается общиы вывод – осток должен быть всегда мпньше делителя.

5.6. Методика изучения свойства "Умножение числа на произведение". Вычислительные приемы.

Подготовительные упражениния : а⦁(в⦁с)

1. Решение примеров 3⦁(4⦁2) = 3⦁8=24

- Как умножить число 3 на произвдение 4 и 2? (Можно найти произв-ие 4 и 2, затем число 3 умн-ть на получ-ый рез-т)

- Рассматрив-ся наглядность.

- Чем яв-ся число 4 в нагляд-ти? (4 число квадратов в одной строке)

- 4 квадратиков в одной строке- это первый множитель.

- Чем яв-ся число 2? (число 2 – это кол-во строк) 2 строки – это второй множитель.

- Что обозначает число 3? (число кржков в одном кв-те) 3 круж. одном кв-те – просто число.

2. Рассмотрение способов вычисления

- Как можно вычислить кол-во кружочков в этих строках? (можно найти кол-во круж. в одной строке, а затем умножить на кол-во строк)

- Как это записать? 3⦁(4⦁2)=(3⦁4)⦁2=24

3. Вывод

- Как можно умн-ть число 3 на произ-ие чисел 4 и 2? (Число 3 умн-ть на первый мн-ль 4, а затем умн-ть умн-ть на второй множитель 2).

4. Общий вывод

- Давайте еще раз рассм-м нагл-ть. Чем яв-ся число 2 в нагл-ти? (число кв-ов в одном столбце)

- 2 кв-ка в одном столбце – это второй множитель.

- Чем яв-ся число 4? (кол-во столбцов) 4 стбца – это первый множитель.

- Что обоз-ет число 3? (кол-во круж.в одном кв-ке)

- 3 круж. в одном кв-те – это просто число.

- Как можно вычислить кол-во круж. в этих строках? (можно найти кол-во кружочков в первом столбце, а затем умн-ть на кол-во столбцов).

- Как это записать? (3⦁2) ⦁ 4=6⦁4=24

- Вывод: Как умн-ть число 3 на произ-ие 4 и 2? (можно число 3 умн-ть на второй множитель 2, а затем умн-ть на первый множ-ль 4)

5. Применение: Умн-ие на числа оканчивающиеся нулями. Н-р: 500⦁40=5 с. (4⦁10)=(5с⦁4)⦁10=20с⦁10=200с=20 000

5.7. МЕТОДИКА ИЗУЧЕНИЯ СВОЙСТВА "УМНОЖЕНИЕ СУММЫ НА ЧИСЛО". ВЫЧИСЛИТЕЛЬНЫЕ ПРИЕМЫ.

1)Подготовительные упр-и: а)решение примеров 2* (5+4) чтение разными способами 2 умн-ть на сумму 5-ти и 4-х. Первый множитель 2, второй мн-ль представляется в виде суммы 5-ти и 4-х где 5 первое слагаемое 4 второе слагаемое. б) Рассмотрение способов вычисления решите выражениявида: 3*(6+2)= 3*8 =24. Уч. Спрашивает как можно умножить ч.3 на сумму 6 и 2 можно найти сумму чисел 6-ти и 2-х, а затем число 3 умножить на полученный результат. Давайте рассмотрим наглядность (1. Строка: шесть закрашенных кружочков и 2 незакрашенных, и такая же вторая и третья строчка) что обозначает число шесть в наглядности? Шесть столбцов красными кружочками. Шесть столбцов крсасным это первое слагаемое. Что обозначает число 2? Это 2 столбца с синими кружочками это второе слагаемое, Что обозначает число 3? Три кружочка в одном столбце – это простое число. Что найдем, когда к 6-ти прибавим 2? Количество столбцов. Что найдем когда 3 умножим на полученный результат?(сколько всего круж в этих столбцах). Как еще по другому можно вычислить это произведение и найти сколько всего кружков в этих столюцах? Что можем найти сеачала? Можем найти сколько красных кружочков. Каким выражением? 3*6 Что найдем затем? Сколько всего синих кружочков? Какими выражением? 3*2, а чтобы найти сколько всего кружочков что нужно сделать? Сложить полученный результат. Походу расссуждения ввыодится запись 3*6 +3*2 =18+6 =24. Как можно умножить число 3 на сумму 6-ти и 2-х? (можно число 3 умножить на первый множитель 6, затем число 3 умножить на 2 мно-ль и .полученный результат сложить. в) Сравните данные записи: 3*(6+2)= 3*8=24 и 3*(6+2)=3*6+3*2 =18+6 =24 Чем они похожи? Чем отличаются? Вычитание одно и тоже выражение получаем одни и те же результаты. г) Общий вывод, значит каким способом моно умножить число на сумму? Можно найти сумму и полученный результат умножить . Можно число умножить на к-ое слагаемое полученне р-ты сложить. д) Первичное закрепление: 1. Рассматривание способов вычисленния по наглядности. 2 упражнение на вычитание двумя способов выраж-ия. 3 упражнение на вычитание выражений удобным спсобом. Примечание: применяется при унможении числа на двух и трехзн-ое

5.8. МЕТОДИКА ИЗУЧЕНИЯ СВОЙСТВА "УМНОЖЕНИЕ ЧИСЛА НА СУММУ". ВЫЧИСЛИТЕЛЬНЫЙ ПРИЕМ. ПРИМЕНЕНИЕ СВОЙСТВА ПРИ УМНОЖЕНИИ МНОГОЗНАЧНЫХ ЧИСЕЛ.

Дата добавления: 2019-07-15; просмотров: 698; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!