ПОНЯТИЕ ДРОБИ. СРАВНЕНИЕ ДРОБЕЙ. ДЕЙСТВИЯ НАД ДРОБЯМИ.
Понятие дроби: Пусть даны отрезок А и единичный отрезок е, причем е яв-ся суммой n отрезок, равных е1. Если отрезок а состоит из m отрезков, равных е1, то его длина может быть представлена в виде (m/n)e. Символ m/n наз-т дробью, в нем m и n – нат-ые числа. Читают символ «эм энных».
Действие над дробями:
1. Дроби, выражающие длину одного и того же отрезка при единице длины е, наз-т равными дробями. (m/n =p/q)
2. Для того, чтобы дроби m/n =p/q были равны, необх-мо и дост-но, чтобы mq=np.
3. Сокращение дробей – это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем. (48/80=3/5).
4. Приведение дробей к ощему знаменателю – это замена дробей равными им дробями, имеющими одинаковые знаменатели. (8/15 и 4/35, разложим 15 и 35 на простые множ-ли 15=3*5, 35=5*7. Тогда 15,35=3*5*7=105, то 8/15=8*7/15*7 = 4/35 = 4*3/35*3=12/105).
Сравнение:
1. Сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.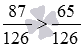 
2. Сравнения дробей с разными знаменателями: если a·d>b·c, то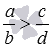 
, а если a·d<b·c, то 
.
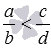3. сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.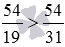 
4. Сравнение обыкновенной дроби с натуральным числом сводится к сравнению двух дробей, если число записать в виде дроби со знаменателем 1.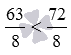 
, следовательно 
|
|
|
ДЕСЯТИЧНЫЕ ДРОБИ. БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ПЕРИОДИЧЕСКИЕ ДРОБИ. ЗАПИСЬ ПОЛОЖИТЕЛЬНЫХ РАЦИОНАЛЬНЫХ ЧИСЕЛ В ВИДЕ ДЕСЯТИЧНЫХ ДРОБЕЙ.
Определение: 341/10² = 3,41; 4/10³ = 0,004. Всякую такую дробь можно записать в виде десятичной дроби. Десятичной называется дробь вида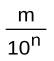 
, где m и n- натуральные числа.
Определение: Если дробь m/n несократима и в разложении знаменателя есть простой множитель, отличный от 2 и 5, то дробь m/n представляется бесконечной десятичной периодической дробью.
Методика преподавания начального курса математики
.
1. МЕТОДЫ ОБУЧЕНИЯ
МЕТОДИКА ПОДГОТОВКИ И ПРОВЕДЕНИЯ САМОСТОЯТЕЛЬНЫХ РАБОТ. МЕСТО И ВРЕМЯ ПРОВЕДЕНИЯ. ВИДЫ.
Самостоятельная работа учащихся - это форма организации их учебной деятельности, осуществляемая под прямым или косвенным руководством преподавателя, в ходе которой учащиеся преимущественно или полностью самостоятельно выполняют различного вида здания с целью развития знаний, умений, навыков и личных качеств.
Иногда она может использоваться при ознакомлени с новым материалом, т.е они самостоятельно воспринимают материал (упражнение), а затем приходят к выводу. В данном случае используется исследовательский метод. Н-р, при изучении табличного умножения дети замечают, что каждый ответ увеличивается на 3.
|
|
|
В зависимости от целей самостоятельные работы можно разделить на:
· обучающие;
· тренировочные;
· закрепляющие;
· повторительные;
· развивающие;
· творческие;
· контрольные.
Дата добавления: 2019-07-15; просмотров: 323; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!