КОМБИНАТОРНЫЕ ЗАДАЧИ, ИХ РЕШЕНИЕ.
ПОНЯТИЕ КОМБИНАТОРНОЙ ЗАДАЧИ. ПРАВИЛА СУММЫ И ПРОИЗВЕДЕНИЯ.
Комбинаторные задачи – это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа.
Правило суммы. Пусть некоторый объект A можно выбрать nn различными способами, а другой объект B можно выбрать m способами. Тогда существует n+mn+m способов выбрать либо объект A, либо объект B.
Задача. На подносе лежат 5 яблок и 3 груши. Сколькими способами можно выбрать фрукт с подноса?
Решение. Яблоко можно выбрать пятью способами. Грушу можно выбрать тремя способами. Стало быть, один из этих фруктов можно выбрать 5 + 3 = 8 способами.
Правило произведения. Пусть объект A можно выбрать n способами и после каждого такого выбора объект B можно выбрать m способами. Тогда выбор пары (A,B) можно осуществить nm способами.
Задача. Имеются три города: A , B и C . Из A в B ведут три дороги, из B в C — пять дорог. Сколько различных путей ведут из A в C ? Прямого пути между A и C нет.
Решение. Обозначим дороги буквами и цифрами. Именно, дороги из A в B назовём a , b , c ; дороги из B в C назовём 1, 2, 3, 4, 5.
Всего получилось 3 · 5 = 15 маршрутов. Как видим, число маршрутов равно произведению числа дорог из A в B на число дорог из B в C .
ЭЛЕМЕНТЫ АЛГЕБРЫ
СООТВЕТСТВИЯ МЕЖДУ ЭЛЕМЕНТАМИ ДВУХ МНОЖЕСТВ
ПОНЯТИЕ СООТВЕТСТВИЯ МЕЖДУ МНОЖЕСТВАМИ. ВЗАИМНООДНОЗНАЧНЫЕ СООТВЕТСТВИЯ. РАВНОМОЩНЫЕ МНОЖЕСТВА.
Соответствием между множествами Х и Y называется любое подмножество R декартова произведения множеств Х и Y, обладающее следующими тремя свойствами:
|
|
|
1) каждому элементу множества X соответствует один и только один элемент множества Y;
2) двум различным элементам множества X всегда соответствуют два различных элемента множества Y;
3) всякий элемент множества Y соответствует хотя бы одному элементу множества X.
Заметим, что первые два свойства дают взаимно однозначные отображения X на некоторое подмножество Y. В этом случае говорят о взаимно однозначном отображении X в Y.
Два множества X и Y, между которыми можно установить взаимно однозначное соответствие, называются равномощными (или эквивалентными), что обозначается символом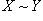 
.
О равномощных множествах говорят также, что они имеют одинаковую мощность. Условимся считать, что пустое множество равномощно только самому себе.
ОТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ОДНОГО МНОЖЕСТВА.
ПОНЯТИЕ ОТНОШЕНИЯ НА МНОЖЕСТВЕ. СВОЙСТВО ОТНОШЕНИЙ.
Множество – определенная совокупность объектов.
Объекты, из которых состоит множество, называются элементами множества .
ПРИМЕР
Множество домов на данной улице, множество натуральных чисел, множество студентов группы и т. д.
|
|
|
Когда говорят о родстве двух человек, Маша и Саша, то подразумевают, что есть некая семья, к членам которой они относятся. Упорядоченная пара (Маша, Саша) отличается от других упорядоченных пар людей тем, что между Машей и Сашей есть некое родство (кузина, отец, и т. д.). В математике среди всех упорядоченных пар декартового произведения А´В двух множеств А и В тоже выделяются некоторые пары в связи с тем, что между их компонентами есть некоторые «родственные» отношения, которых нет у других.
Отношением (бинарным отношением, двуместным отношением)из множества A в множество B называется некоторое подмножество декартового произведения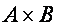 
Отношения в дальнейшем будем обозначать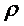 
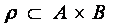
(читается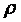 
отношение из A в B)
Есл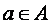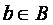и 
, 
и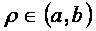 
, то говорят, что a находится в отношении с b. Используется также запись
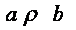
ПРИМЕР
Если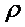 
отношение из A в A ( 
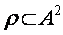), то говорят 
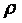бинарное отношение на множестве A .
ПРИМЕР
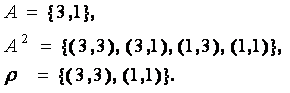
n -арным отношением на множестве А, называется некоторое подмножество n-ой степени множества A.
ПРИМЕР
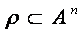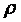, − n-арное отношение на множестве А.
Виды бинарных отношений на множестве A
1) Обратное отношение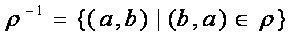 
.
2) Дополнение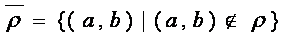 
.
3) Тождественные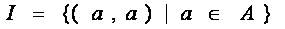 
.
4) Универсальные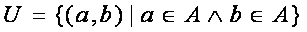 
.
Дата добавления: 2019-07-15; просмотров: 948; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!