ОТНОШЕНИЕ СЛЕДОВАНИЯ И РАВНОСИЛЬНОСТИ МЕЖДУ ПРЕДЛОЖЕНИЯМИ. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ.
Любое рассуждение не обходится без слов «следовательно», «из данного предложения следует», «отсюда вытекает».
Говорят, что из предложения А следует предложение В, если всякий раз, когда истинно предложение А, истинно и предложение В.
Если из предложения А следует предложение В, а из предложения В следует предложение А, то говорят, что предложения А и В равносильны.
Понятие отношения следования между предложениями позволяет уточнить смысл слов «необходимо» и «достаточно», которые часто употребляются в математике.
Если из предложения А следует предложение В, то говрят, что В- необходимое условие для А, а А- достаточное для В.Другими словами, предложение В называется необходимым условием для А, если оно логически следует из А. Предложение А называют достаточным условием для В, если В из него следует.
А В (В- необходиоме условие для А; А- необходимое условие для В).
Если предложения А и В равносильны, то говорят, что А- неоходимое и достаточное условие для В, и наоборот.
СТРОЕНИЕ ТЕОРЕМЫ. ВИДЫ ТЕОРЕМ.
Теорема – это высказывание, истинность которого устанавливается посредством рассуждения (доказательства).
В записи теоремы можно выделить 3 части:
1) разъяснительную – в ней описываются множества объектов, о которых идет речь в теореме;
2) условие теоремы: предикат заданный на множестве Х;
3) заключение теоремы: предикат В (х), заданный на множестве Х.
|
|
|
Виды теорем:
Теорема, обратной данной.
«В равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник – равнобедренный». Это истинное предложение и потому является теоремой.
2. Теорема, противоположная данной.
Для любой теоремы вида А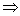 
В (если А, то В) можно сформулировать предложение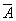 
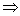
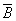(если не А, то не В), которое называют противоположным данному. Но это предложение также не всегда является теоремой.
Например, предложение, противоположное теореме «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником» будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».
3. Теорема, обратно противоположной данной.
Для всякой теоремы вида А 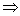В (если А, то В) можно сформулировать предложение 
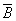
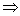
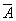(если не В, то не А), которое называют обратным противоположному. Например, для теоремы «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником» предложение, обратное противоположному, будет таким: «если в четырехугольнике диагонали не равны, то он не является прямоугольником». Это, как известно, предложение истинное, и, следовательно, является теоремой, обратно противоположной данной.
|
|
|
Дата добавления: 2019-07-15; просмотров: 972; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!