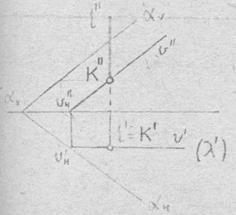
Определение точки пересечения прямой с плоскостью (плоскость - общего положения, прямая - проецирующая)
 | |||
 |
а б
Рис. 4.10
4.8
В первом примере (рис.4.10,а) прямая l является горизонтально-проецирующей прямой, во втором (рис.4.10,б) - фронтально-проецирующей прямой.
Как и в предыдущей задаче одну проекцию точки пересечения прямой с плоскостью видим сразу (К' в задании 4.10,а и К" в задании 4.10,б), т.е. из условия ее принадлежности проецирующей фигуре - прямой.
Вторую проекцию точки находим из условия ее принадлежности фигуре общего положения - плоскости.
Если угодно, то можно говорить о построении второй проекции точки с помощью вспомогательной секущей плоскости λ.
Но, как видно из чертежа, оба решения будут графически совпадать.
Окончанием решения задачи, как и во всех предыдущих случаях, будет выделение видимых и невидимых участков прямой.
Содержание лекции № 4 изложено в учебнике С.А.Фролова на стр. 118-124 .
Локтев О.В. стр.26-27, 32-36
РАЗДЕЛ №2.
Преобразование комплексного чертежа ( Лекции №№ 5,6 )
ЛЕКЦИЯ №5
Тема лекции:
Способы преобразования комплексного чертежа
Содержание лекции
Общие понятия. Способ перемены плоскостей проекций. Способ плоскопараллельного перемещения.
Общие понятия
Из изложенного на предыдущих лекциях материала легко установить, что проекции прямой, плоскости или фигуры, находящейся в случайном положении относительно плоскостей проекций, не всегда удобны для решения той или иной конкретной задачи. Например, проекции отрезка, расположенного наклонно ко всем плоскостям проекций, не дают непосредственного представления о его натуральной длине. Можно сказать поэтому, что в данном случае проекции отрезка "неудобны" для решения поставленного вопроса. Между тем, если бы тот же отрезок был параллелен одной из плоскостей проекций, он проецировался бы на эту плоскость без искажения и мы могли бы судить о его действительной длине без всяких дополнительных построений. При таком положении отрезка можно считать его проекции "удобными" для решения интересующего нас вопроса.
Можно привести много примеров подобного рода.
Студент, изучивший предыдущие лекции, сумеет и сам найти ряд других примеров, подтверждающих, что при одном расположении на эпюре заданных элементов задача решается сложнее, а при другом - проще.
Способы преобразования чертежа, которые нам предстоит изучит, как раз и создают возможность так изменить проекционный чертеж, чтобы геометрическая фигура (фигуры) после преобразования заняла такое частное положение, которое давало бы решение поставленной задачи или значительно его упрощало.
При любом способе преобразования чертежа, мы должны различать и уметь выполнять следующие четыре основные задачи.
5.2
1. Преобразование прямой общего положения в прямую уровня.
2. Преобразование прямой общего положения в проецирующую прямую.
3. Преобразование плоскости общего положения в проецирующую плоскость.
4. Преобразование плоскости общего положения в плоскость уровня.
Эти четыре основные задачи на преобразование чертежа будут в дальнейшем, при решении метрических и позиционных задач, играть исключительно важную роль.
Переход от общего положения геометрической фигуры к частному можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости проекций. При сохранении ортогонального проецирования этого можно достичь двумя принципиально различными путями. Во-первых, введением новых плоскостей проекций, по отношению к которым проецируемая фигура, не изменяющая при этом своего положения в пространстве, окажется в частном положении. Во-вторых, перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, остающихся неподвижными и не меняющими своего положения в пространстве.
Первый путь лежит в основе способа перемены плоскостей проекций, второй составляет теоретическую базу способа плоскопараллельного перемещения. Рассмотрим эти способы.
Дата добавления: 2019-03-09; просмотров: 384; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
