Прямая принадлежит плоскости в том случае, если следы этой прямой принадлежат одноименным следам данной плоскости.
3.5
Это правило легко устанавливается из рассмотрения рис.3.4.
Плоскость общего положения
Плоскость, случайным образом расположенная в пространстве, т.е. имеющая произвольные углы наклона к плоскостям проекций, называется плоскостью общего положения.
Все плоскости, изображенные на предыдущих чертежах - 3.1, 3.2, 3.3, 3.4, являются плоскостями общего положения.
Плоскость частного положения
Плоскость, перпендикулярная или параллельная плоскости проекций, называется плоскостью частного положения.
Плоскость, перпендикулярная к плоскости проекций
Плоскость, перпендикулярная к плоскости проекций, называется проецирующей плоскостью.
а б в
Рис. 3.5
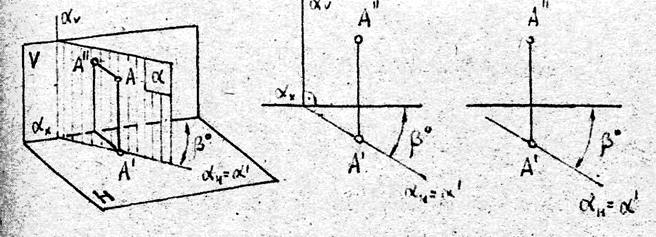
На рис.3.5 изображена плоскость a, перпендикулярная к горизонтальной плоскости проекций Н. Такая плоскость называется горизонтально-проецирующей плоскостью.
Горизонтальная проекция точки А, как и всех точек этой плоскости a, будет лежать на aH - горизонтальном следе этой плоскости.
3.6
Следовательно, в данном и только данном случае, горизонтальный след плоскости будет представлять собой горизонтальную проекцию плоскости, т.е. проекцию всех её точек. Поэтому, эта линия - не только след плоскости - aH, но и её горизонтальная проекция - a '.
Второй след проецирующей плоскости всегда перпендикулярен оси проекций (рис.3.5а,б), и, поскольку мы наперед знаем его положение, этот след можно на чертеже не изображать.
|
|
|
По этой причине проецирующую плоскость рационально, что мы и будем делать в дальнейшем, задавать только одним следом, как это показано на рис. 3.5,в.
Угол наклона, горизонтально-проецирующей плоскости a к плоскости проекций V - угол b°, на чертеже мы видим в натуральную величину.
| |
Такую плоскость мы будем называть фронтально-проецирующей плоскостью.
Угол наклона плоскости b к горизонтальной плоскости проекций Н - угол a °, мы видим на чертеже в натуральную величину.
Рис.3.6
Плоскость, параллельная плоскости проекций
Плоскость, параллельная плоскости проекций называется плоскостью уровня.
 |  | ||
а б
Рис. 3.7.
3.7
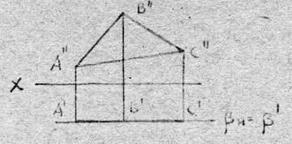
На рис. 3.7 изображены плоскости, параллельные одной из плоскостей проекций.
Плоскость, параллельная плоскости проекций, вместе с тем перпендикулярна к двум другим плоскостям. Её, иногда, называют поэтому "двоякопроецирующей". Эта плоскость обладает всеми свойствами проецирующей, по отношению, к тем плоскостям проекций, к которым она перпендикулярна.
|
|
|
На рис. З.7,а приведена плоскость a, параллельная горизонтальной плоскости проекций. Такая плоскость называется горизонтальной плоскостью.
Эта плоскость будет перпендикулярна к плоскости проекций V, поэтому она может быть задана как обычная проецирующая плоскость.
На рис. 3.7б изображена плоскость b, с принадлежащим ей треугольником ABC, параллельная фронтальной плоскости проекций. Такую плоскость мы будем называть фронтальной.
Примечание.
материал параграфа 3.6 "Плоскость частного положения" на лекции излагается не полностью. Часть этого материала, как например,- "профильно-проецирующие плоскости", будет рассмотрена на практических занятиях.
Особые линии плоскости
К особым линиям плоскости относятся линии уровня, т.е. прямые, принадлежащие данной плоскости, одновременно, параллельные одной, из плоскостей проекций.
 |
а б
Рис. 3.8
На рис. 3.8 показана линия h , принадлежащая плоскости a и параллельная плоскости проекций Н. На рис. 3.8,а дано наглядное изображе-
|
|
|
3.8
ние, на рис. 3.8,б - эпюр этой прямой.
Прямая h называется горизонталью плоскости a. В любой плоскости можно провести множество горизонталей. Все они будут параллельны между собой.
Горизонтальный след aH плоскости a тоже является горизонталью плоскости a. Следовательно:
h||H Þ (h'|| aH)Ù(h"|| х).
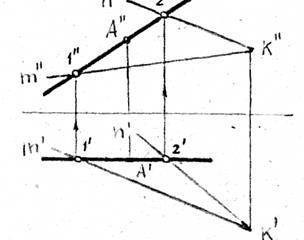
На рис. 3.9 приведено изображение фронтали плоскости b, заданной следами (рис.3.9,а) и пересекающимися прямыми m и n (рис.3.9,б).
 |
а б
Рис. 3.9
Точка А во всех рассмотренных случаях принадлежит заданной плоскости, т.к. она принадлежит либо горизонтали плоскости (рис.3.8), либо фронтали плоскости (рис.3.9).
Параллельность плоскостей
Дата добавления: 2019-03-09; просмотров: 355; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!