Если плоскости параллельны, то двум пересекающимся прямым одной плоскости соответственно параллельны дне пересекающийся прямые другой плоскости.
 | |||
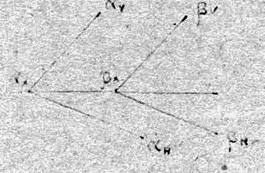 | |||
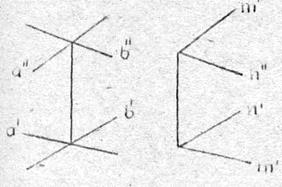
Рис. 3.10 Рис. 3.11
3.9
Две плоскости a (a ∩ b) и b (m ∩ n) (рис.3.10) параллельны между собой, т.к. прямая a параллельна прямой m, а прямая b параллельна прямой n.
Если плоскости заданы следами (рис.3.11), то определение параллельности плоскостей будет выглядеть так.
Если плоскости параллельны, то их одноименные следы будут также параллельны.
Прямая, параллельная плоскости
Прямая будет параллельна плоскости в том случае, если в плоскости найдется прямая, параллельная данной.
 Задача.
Задача.
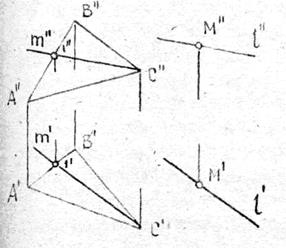
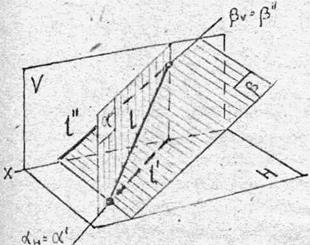
Дана точка М и фронтальная проекция прямой l, проходящей через эту точку. Построить горизонтальную проекцию прямой l, зная, что эта прямая параллельна заданной плоскости a(ΔА B С). (См. рис. 3.12).
Строим в плоскости треугольника прямую m, параллельную прямой l и находим направление горизонтальной проекции прямой l.
Рис.3.12
Содержание лекции изложено в учебнике С.А.Фролова на стр. 78-85 ; 173-175.
ЛЕКЦИЯ №4
Тема лекции
Комплексный чертеж плоскости (продолжение)
Содержание лекции
Взаимное пересечение двух плоскостей. Построение линии их пересечения. Пересечение прямой с плоскостью. Построение точки пересечения прямой с плоскостью.
Взаимное пересечение двух плоскостей
В конце прошлой лекции мы рассмотрели случай взаимной параллельности двух плоскостей.
|
|
|
Если плоскости не будут параллельны, они будут пересекаться. Возникает одна из основных позиционных задач - отыскание (построение) линии пересечения двух плоскостей.
При решении последней задачи следует рассмотреть различные случаи расположения пересекающихся плоскостей относительно плоскостей проекций. Здесь могут быть 4 случая.
1. Обе пересекающиеся плоскости - одноименно проецирующие.
2. Пересекающиеся плоскости - разноименно проецирующие.
3. Одна из пересекающихся плоскостей - плоскость общего положения, другая - проецирующая.
4. Обе пересекающиеся плоскости являются плоскостями общего положения.
Рассмотрим эти случаи в том порядке, как они здесь перечислены.
Построение линии пересечения двух плоскостей, если обе плоскости - одноименно проецирующие
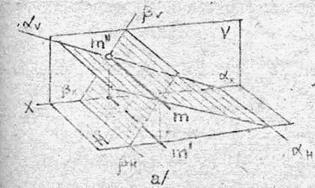 | 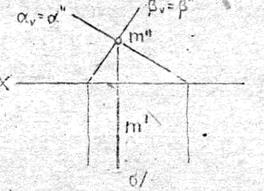 | ||
Рис. 4.1
4.2
На рис.4.1 даны пересекающиеся фронтально-проецирующие плоскости a и b.
Их линия пересечения - прямая m будет также фронтально-проецирующей прямой.
На комплексном чертеже (рис.4.1,б) фронтальная проекция прямой в виде точки m " имеется, надо лишь её обозначить.
Горизонтальная проекция линии пересечения - m ' строится из условия, что m - фронтально-проецирующая прямая.
|
|
|
Построение линии пересечения двух плоскостей, если плоскости - разноименно проецирующие
 | |||
 | |||
а б
Рис 4.2
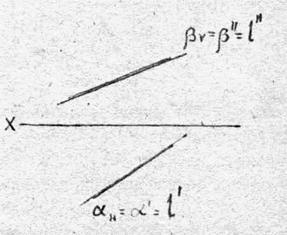
На рис. 4.2 даны горизонтально-проецирующая плоскость a и фронтально-проецирующая плоскость b, которые пересекаются по прямой l.
На комплексном чертеже (рис.4.2, б) проекции этой прямой уже имеются (они совпадают с одноименными проекциями плоскостей) и эти проекции следует лишь обозначить.
Дата добавления: 2019-03-09; просмотров: 467; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
