Способы изображения плоскости на комплексном чертеже
Если спроецировать все точки плоскости, то множество проекций точек плоскости покроет всю плоскость проекций, т.е. мы не получим на ней никакого изображения.
Только в единственном случае можно получить изображение плоскости посредством проецирования всех ее точек. Это произойдет тогда, когда проецирующие лучи будут направлены вдоль изображаемой плоскости. При ортогональном проецировании такое изображение, очевидно, может получиться только в том случае, когда изображаемая плоскость будет расположена перпендикулярно к плоскости проекций.
Как же задать комплексный чертеж плоскости?
 |  | 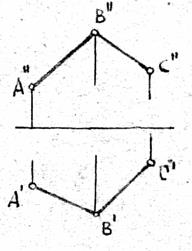 | |||
а б г
Рис. З.1
Из элементарной геометрии известно, что положение плоскости вполне определяется, если заданы принадлежащие этой плоскости:
а) три точки, не лежащие на одной прямой;
3.2
б) прямая и точка вне этой прямой;
в) две параллельные прямые;
г) две пересекающиеся прямые;
д) любая плоская фигура.
Также и на комплексном чертеже любая из перечисленных комбинаций геометрических фигур определяет собой плоскость.
На рис.3.1 приведены варианты а), б), г) задания плоскости.
При рассмотрении всех вышеперечисленных вариантов задания плоскости, легко заметить, что все они, в сущности, сводятся к одному способу - заданию плоскости тремя точками.
Ещё один способ задания плоскости - ее следами, мы рассмотрим чуть ниже.
Принадлежность прямой плоскости
Прямая принадлежит плоскости в том случае, если эта прямая:
а) имеет с плоскостью две общие и нетождественные точки,
б) имеет с плоскостью одну общую точку и эта прямая параллельна другой прямой, принадлежащей этой плоскости.
 | |||||
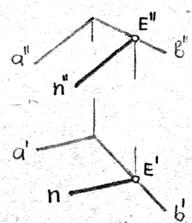 | |||||
 | |||||
а б в
Рис. 3.2
Примеры.
Плоскость a задана пересекающимися прямыми a и b (рис.3.2). Прямая l принадлежит плоскости a, т.к. имеет с ней две общие точки А и В (рис.3.2а).
Прямая m принадлежит плоскости a, т.к. имеет с ней общую точку К и эта прямая параллельна прямой C, принадлежащей плоскости a (рис.3.2,б).
3.3
Прямая n принадлежит плоскости a , т.к. имеет с ней общую точку Е и эта прямая параллельна прямой а (рис.3.2,в).
Принадлежность точки плоскости
Точка принадлежит плоскости в том случае, если она лежит на прямой, принадлежащей этой плоскости.
Пример
Дана фронтальная проекция точки М. Построить горизонтальную проекцию этой точки, если известно, что точка М принадлежит плоскости треугольника ABC (рис.3.3).
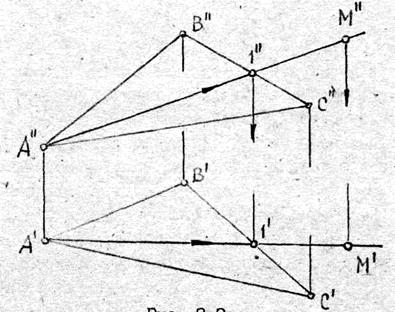
Рис. 3.3
Положение точки М можно определить с помощью любой прямой, проходящей через точку М и принадлежащей плоскости треугольника. В нашем примере в качестве такой прямой взята прямая AM.
Следы плоскости
Следами плоскости называются линии пересечения данной плоскости с плоскостями проекций.
На рис.3.4 приведено наглядное изображение плоскости a, заданной следами (рис.3.4,а) и её изображение на комплексном чертеже (рис.3.46).
a H - горизонтальный след плоскости a,
3.4
av - фронтальный след плоскости a,
ax - точка схода следов плоскости a.
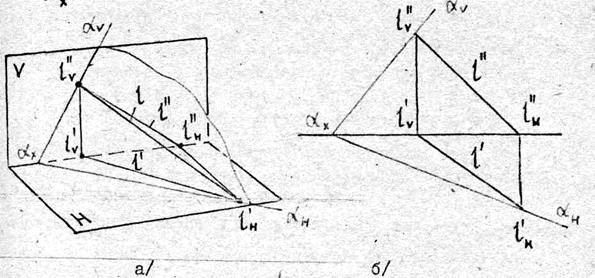 |
Рис. 3.4
Задание плоскости следами, по своей сути, является обычным заданием плоскости пересекающимися прямыми. Но, в данном случае, это не случайные, а такие прямые, которые, помимо данной плоскости, принадлежат еще и плоскостям проекций.
В начертательной геометрии охотно пользуются заданием плоскости её следами, т.к. такое задание:
а) обладает, по сравнению с другими способами, большей наглядностью, т.к. по расположению следов на эпюре легко судить и о расположении самой плоскости в пространстве;
б) наиболее рационально, т.к. требует для задания плоскости построения всего двух прямых.
Обратить внимание на особенности задания плоскости следами:
а) Следы плоскости выполняются тонкими сплошными линиями, такими же, как линии связи и оси проекций;
б) На чертеже даются обозначения самих следов, а их проекции, одна из которых совпадает с самим следом, а другая - с осью проекций, не обозначаются;
в) Следы обозначаются той же буквой, что и сама плоскость, с добавлением индекса той плоскости проекций, которой этот след принадлежит.
Принадлежность прямой плоскости, заданной следами, может быть определена следующим образом:
Дата добавления: 2019-03-09; просмотров: 751; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
