Построение линии пересечения двух плоскостей, если одна из них - плоскость общего положения, другая - проецирующая

На рис. 4.3 даны горизонтально-проецирующая плоскость a  и плоскость общего положения b, которые пересекаются по прямой l.

На рис. 4.4 плоскость общего положения a, заданная, треугольником ABC, пересекается с фронтально-проецирующей плоскостью b.

 

 

4.3

 

                Рис. 4.3                                                    Рис. 4.4                    

В обоих случаях одна проекция линии пересечения плоскостей определяется сразу из условия её принадлежности проецирующей плоскости, это - l ' на рис.4.3 и l " на рис.4.4. Другая - проекция линии пересечения легко определяется из условия её принадлежности плоскости общего положения.

При решении задачи на построение линии пересечения плоскостей приходиться решать и вопрос видимости фигур. Так в задаче, приведенной на рис.4.4, на горизонтальной проекции часть треугольника ABC, лежащая ниже плоскости b, будет невидимой.

Рассматривая вышеприведенные задачи можно сделать вывод, что построение линии пересечения плоскостей, в том случае, когда хотя бы одна из плоскостей является проецирующей, является очень простой задачей.

По этой причине в дальнейшем, когда при решении большого круга позиционных задач, мы будем вынуждены широко пользоваться вспомогательными секущими плоскостями, в качестве последних мы, как правило, будем использовать проецирующие плоскости.

Следующая задача явится примером такого применения проецирующих плоскостей.

Построение линии пересечения двух плоскостей, если обе из них являются плоскостями общего положения

Поскольку линией пересечения двух плоскостей является прямая, то для её построения необходимо найти какие-либо две точки этой прямой.

 

 

4.4

На рис. 4.5,а показано как, при помощи двух вспомогательных секущих плоскостей λ₁ и λ₂, может быть найдена линия пересечения плоскостей a и b - прямая l . Плоскость λ₁дает точку М этой прямой, плоскость λ₂- точку N.

 

 

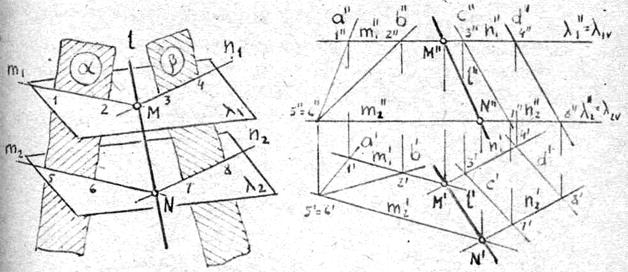а                                                            б

Рис. 4.5

На рис. 4.5,б приведено решение этой задачи, с помощью того, же принципа, на комплексном чертеже. Здесь плоскость a задана пересекающимися прямыми а и b, а плоскость b  - параллельными прямыми c и d.

В качестве секущих плоскостей выбраны фронтально-проецирующие плоскости λ₁ и λ₂. В данном случае эти плоскости являются горизонтальными, но они могли бы ими и не быть.

Если плоскости λ₁ и λ₂ взяты параллельными, то линии их пе­ресечения с плоскостями a и b будут также соответственно па­раллельны, т. е. (1, 2)||(5, 6) и (3, 4)||(7, 8).

На рис. 4.6 показано построение линии пересечения плоскостей a  и b, заданных следами. Следы плоскостей в пределах чертежа пересекаются.

Рис. 4.6

В этом случае при отыскании линии пересечения заданных плоскостей нет необходимости прибегать к помощи вспомогательных секущих

 

 

4.5

плоскостей, т.к. их роль выполняют сами плоскости проекций.

Если же следы плоскостей в пределах чертежа не пересекаются, тогда, как и в общем случае, при решении задачи следует использовать вспомогательные секущие плоскости.

---

Дата добавления: 2019-03-09; просмотров: 786; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!