Повний диференціал першого порядку
Повний приріст функції (7.1) має вигляд:
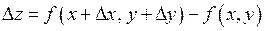 , (7.2)
, (7.2)
де  і
і 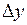 – довільні прирости незалежних змінних.
– довільні прирости незалежних змінних.
Функцію  називають диференційованою в точці називають диференційованою в точці  , якщо виконуються умови:
1) в точці , якщо виконуються умови:
1) в точці  існують частинні похідні першого порядку існують частинні похідні першого порядку 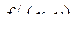 і і 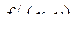 ;
2) повний приріст функції (3.1) в точці ;
2) повний приріст функції (3.1) в точці  можна представити як можна представити як
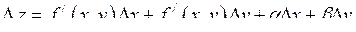 , (7.3)
де , (7.3)
де 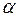 і і  прямують до нуля при прямують до нуля при 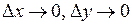 , тобто , тобто 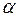 і і  є нескінченно малими при є нескінченно малими при 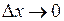 і і 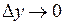 , або що теж саме при , або що теж саме при 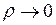 , де , де 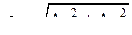 – відстань між точками – відстань між точками  і і 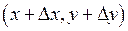 . .
|
З умови 1) існування частинних похідних не завжди випливає умова 2). Функція (7.1) може мати частинні похідні, але не бути диференційованою. Тут порушується аналогія з функцією однієї змінної, для якої наявність похідної забезпечує диференційованість функції.
| Теорема 7.2. | (ознака диференційованості функції) Якщо в деякому околі точки  функція функція  має перші частинні похідні, які є неперервними в точці має перші частинні похідні, які є неперервними в точці  , то функція , то функція 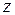 диференційована в цій точці. диференційована в цій точці.
|
Якщо функція (7.1) диференційована в точці  , то її повним диференціалом першого порядку в цій точці називають величину, лінійну відносно , то її повним диференціалом першого порядку в цій точці називають величину, лінійну відносно  і і 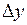 : :
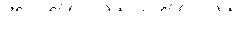 . (7.4) . (7.4)
|
Нехай 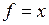 , тоді
, тоді 
 . Значить,
. Значить, 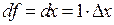 , отже
, отже 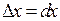 .
.
Нехай 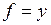 , тоді
, тоді 
 . Отже,
. Отже, 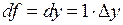 ,
, 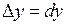 .
.
Тому повний диференціал функції двох змінних  можна записати у вигляді:
можна записати у вигляді:
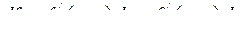 . (7.5)
. (7.5)
| Приклад 7.4. | Знайти повний диференціал функції 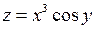 . .
|
|
|
|
Розв’язання. Обчислимо спочатку частинні похідні першого порядку:
 .
.
Частинні похідні є всюди неперервними функціями. Тому функція  буде всюди диференційованою. Її повний диференціал має вигляд:
буде всюди диференційованою. Її повний диференціал має вигляд:
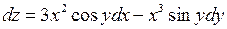 .
.
Похідна неявної, складної функції. Похідна за напрямом
Похідна складної функції
Нехай  і
і  . Тоді з формули (7.5) випливає вигляд похідної від функції однієї змінної
. Тоді з формули (7.5) випливає вигляд похідної від функції однієї змінної 
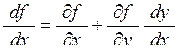 . (7.6)
. (7.6)
Це формула повної похідної.
| Приклад 7.5. | Знайти повну похідну функції 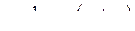 , якщо , якщо  . .
|
Розв’язання. За формулою (7.6) маємо:
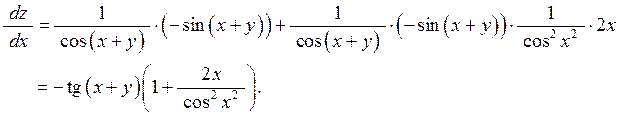
Похідна від неявної функції
Нехай відношення 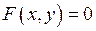 задає неявно функцію
задає неявно функцію 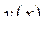 . Позначимо
. Позначимо 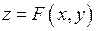 і
і 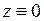 , застосуємо формулу (7.6) і одержимо:
, застосуємо формулу (7.6) і одержимо:
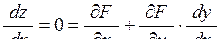 . Тоді при
. Тоді при 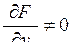 маємо:
маємо:
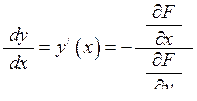 . (7.7)
. (7.7)
| Приклад 7.6. | Знайти похідну функції 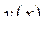 , заданої відношенням , заданої відношенням 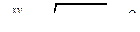 . .
|
Розв’язання. Згідно формули (7.7) одержимо:
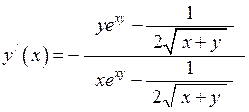 .
.
Похідна за напрямом
Градієнтом функції 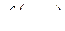 називають вектор називають вектор
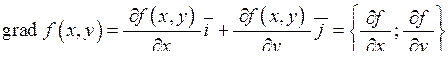 . (7.8) . (7.8)
|
Градієнт вказує напрямок найбільшого зростання функції.
Похідна функції 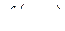 за напрямом вектора за напрямом вектора 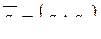 , в точці , в точці  виражається формулою: виражається формулою:
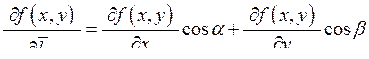 , (7.9)
де напрямні косинуси вектора , (7.9)
де напрямні косинуси вектора 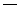
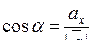 , , 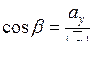 . (7.10) . (7.10)
|
|
|
|
Найбільше значення похідної за напрямом дорівнює модулю градієнта, знайденому у відповідній точці 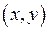 :
:
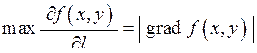 . (7.11)
. (7.11)
| Приклад 7.7. | Знайти градієнт і похідну за напрямом, який визначають градієнтом, функції 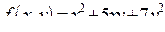 в точці в точці 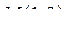 . .
|
Розв’язання. За формулою (7.8) знайдемо градієнт заданої функції у визначеній точці:
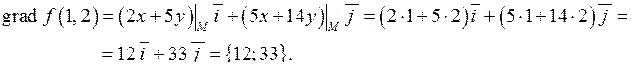
В напрямку градієнта функція буде мати похідну: 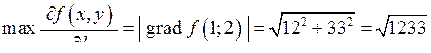 .
.
Похідна за напрямом, знайдена за всяким іншим напрямом, буде менше знайденого значення.
Контрольні питання зі змістового модуля III
| 6.1. | Дати означення похідної функції однієї змінної, диференційованості функції в точці та на інтервалі. |
| 6.2. | Який геометричний зміст похідної? |
| 6.3. | Який зв’язок між диференційованістю та неперервністю функції? Чи випливає з неперервності функції її диференційованість? |
| 6.4. | Навести основні властивості похідної, зокрема формули добутку та частки функцій, похідної складної та оберненої функцій. |
| 6.5. | Дати означення похідної вищих порядків. |
| 6.6. | Навести формули похідних основних елементарних функцій. |
| 6.7. | Як знайти похідну функції, що задана параметрично? Похідну функції, що задана неявно? |
| 6.8. | Коли застосовують та у чому полягає логарифмічне диференціювання? |
| 6.9. | Дати означення диференціала функції однієї змінної, навести зв’язок між похідною та диференціалом та його властивості. |
| 6.10. | Який геометричний зміст диференціала? |
| 6.11. | У чому полягає інваріантність форми диференціала першого порядку? |
| 7.1. | Дати означення частинних похідних та навести їх геометричний зміст. |
| 7.2. | Сформулювати теорему про змішані похідні. |
| 7.3. | Дати означення диференційованості функції двох змінних. |
| 7.4. | Навести ознаку диференційованості функції двох змінних. |
| 7.5. | Як знайти повний диференціал функції двох змінних? |
| 7.6. | Дати означення градієнта функції двох змінних. |
| 7.7. | Як знайти похідну за напрямом функції двох змінних? |
| 7.8. | Який вектор вказує напрямок найбільшого зростання функції? Яким є найбільше значення похідних у точці за напрямом? |
|
|
|
Дата добавления: 2019-02-13; просмотров: 214; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
