Порівняння нескінченно малих функцій
Нехай  і
і  – нескінченно малі функції при
– нескінченно малі функції при 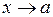 , причому
, причому 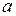 може бути як числом, так одним з символів
може бути як числом, так одним з символів  . Тоді справедливі наступні означення.
. Тоді справедливі наступні означення.
Якщо  , то функцію , то функцію  називають нескінченно малою функцією вищого порядку мализни в порівнянні з функцією називають нескінченно малою функцією вищого порядку мализни в порівнянні з функцією  , а функцію , а функцію  називають нескінченно малою функцією нижчого порядку мализни в порівнянні з функцією називають нескінченно малою функцією нижчого порядку мализни в порівнянні з функцією  . .
|
Якщо  , то функцію , то функцію  називають нескінченно малою функцією нижчого порядку мализни в порівнянні з функцією називають нескінченно малою функцією нижчого порядку мализни в порівнянні з функцією  , а функцію , а функцію  називають нескінченно малою функцією вищого порядку мализни в порівнянні з функцією називають нескінченно малою функцією вищого порядку мализни в порівнянні з функцією  . .
|
Якщо  і і  , ,  , то функції , то функції  та та  називають функціями одного порядку мализни. називають функціями одного порядку мализни.
|
Якщо  , то нескінченно малі функції , то нескінченно малі функції  і і  називають еквівалентними. Позначення: називають еквівалентними. Позначення:  . .
|
Якщо  і і  , ,  , то функцію , то функцію  називають нескінченно малою функцією називають нескінченно малою функцією  -го порядку мализни відносно нескінченно малої функції -го порядку мализни відносно нескінченно малої функції  . .
|
| Теорема 4.1. | Границя відношення двох нескінченно малих функцій не зміниться, якщо кожну з них або яку-небудь одну замінити еквівалентними ним. |
При обчисленні границь функцій зручно користуватися теоремою 17 і наступними основними еквівалентностями.
Основні еквівалентності при 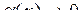







| Приклад 4.21. | Довести, що функції  і і  при при  є нескінченно малими одного порядку. є нескінченно малими одного порядку.
|
Розв’язання. Знайдемо границю відношення заданих функцій:
|
|
|
 ,
, 
Таким чином, дані функції є нескінченно малими одного порядку.
| Приклад 4.22. | Чи є еквівалентними функції  і і  при при  ? ?
|
Розв’язання. Знайдемо границю відношення цих функцій:
 .
.
Таким чином, функція  є нескінченно малою вищого порядку, ніж функція
є нескінченно малою вищого порядку, ніж функція  тобто дані функції не є еквівалентними.
тобто дані функції не є еквівалентними.
| Приклад 4.23. | Довести, що нескінченно малі функції  і і 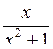 при при  є еквівалентними. є еквівалентними.
|
Розв’язання. Очевидно, що  . Отже,
. Отже,  і
і 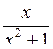 при x ® 0 є еквівалентними.
при x ® 0 є еквівалентними.
| Приклад 4.24. | Знайти  . .
|
Розв’язання. При  функція
функція  є нескінченно малою. Оскільки при заміні нескінченно малої функції
є нескінченно малою. Оскільки при заміні нескінченно малої функції  еквівалентною їй функцією
еквівалентною їй функцією  за теоремою 4.1. границя відношення не зміниться, то
за теоремою 4.1. границя відношення не зміниться, то
 .
.
| Приклад 4.24. | Знайти 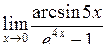 . .
|
Розв’язання. Оскільки при x®0  , а
, а 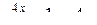 і оскільки за теоремою 4.1 границя відношення не зміниться, то
і оскільки за теоремою 4.1 границя відношення не зміниться, то
 .
.
| Приклад 4.25. | Знайти  . .
|
Розв’язання. Тут чисельник і знаменник – нескінченно малі функції, проте, х не є нескінченно малою функцією, оскільки  , а не до нуля. Введемо нескінченно малу
, а не до нуля. Введемо нескінченно малу  , тоді
, тоді  . Маємо
. Маємо
 .
.
Неперервність функції
Неперервність функції в точці і на відрізку
Функцію 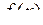 , що визначена в деякому околі точки , що визначена в деякому околі точки 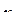 , називають неперервною в точці , називають неперервною в точці 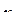 , якщо:
1) вона визначена в точці , якщо:
1) вона визначена в точці 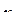 , тобто існує , тобто існує  ;
2) існує границя функції при ;
2) існує границя функції при  , що прямує до , що прямує до 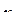 , тобто існує , тобто існує  ;
3) ця границя дорівнює значенню функції в точці х0, тобто ;
3) ця границя дорівнює значенню функції в точці х0, тобто
 . .
|
|
|
|
Наведемо означення неперервності функції, яке є еквівалентним попередньому, і засноване на понятті нескінченно малої величини. Дамо аргументу 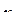 приріст
приріст  , тоді функція
, тоді функція 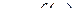 отримає приріст
отримає приріст
 .
.
Функцію 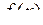 називають неперервною в точці називають неперервною в точці 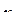 , якщо вона визначена в цій точці і нескінченно малому приросту аргументу , якщо вона визначена в цій точці і нескінченно малому приросту аргументу  відповідає нескінченно малий приріст функції відповідає нескінченно малий приріст функції  , тобто , тобто
 . .
|
| Зауваження. | Визначення неперервності функції 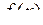 в точці в точці 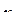 може бути записане так: може бути записане так:
 ,
тобто для неперервної функції можлива перестановка символів границі і функції. ,
тобто для неперервної функції можлива перестановка символів границі і функції.
|
| Зауваження. | Друга умова неперервності функції означає зокрема, що
 . .
|
Дата добавления: 2019-02-13; просмотров: 370; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
