Границя числової послідовності та функції.
ОСНОВНІ пОНЯТТЯ
Функціональна залежність. Огляд основних елементарних функцій
В курсі вищої математики розглядають досить важливі властивості функцій, які складно досліджувати елементарними способами. У основі методів, за допомогою яких доцільно досліджувати ці нові властивості, лежить поняття границі функції, одне з фундаментальних понять сучасної математики.
Функцією 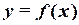 називають відповідність, за якою кожному елементу x з множини D відповідає деякий єдиний елемент з множини E. називають відповідність, за якою кожному елементу x з множини D відповідає деякий єдиний елемент з множини E.
|
Незалежну змінну x називають аргументом, а величину у – функцією. Множину D називають областю визначення функції і позначають 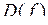 . Множину E називають областю значень функції і позначають . Множину E називають областю значень функції і позначають  . Якщо . Якщо 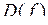 і і 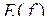 – числові множини, то функцію називають числовою. – числові множини, то функцію називають числовою.
|
Функцію 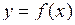 називають парною, якщо для будь-яких значень х з області визначення D виконується рівність називають парною, якщо для будь-яких значень х з області визначення D виконується рівність 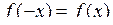 , причому , причому 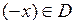 .
Функцію .
Функцію 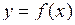 називають непарною, якщо для будь-яких значень х з області визначення D виконується рівність називають непарною, якщо для будь-яких значень х з області визначення D виконується рівність 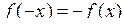 , причому , причому 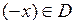 . .
|
У інших випадках функцію 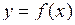 називають функцією загального вигляду. Графік парної функції є симетричним відносно осі ординат, графік непарної функції є симетричним відносно початку координат.
називають функцією загального вигляду. Графік парної функції є симетричним відносно осі ординат, графік непарної функції є симетричним відносно початку координат.
Функцію 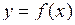 називають зростаючою на деякому проміжку Х, якщо більшому значенню аргументу з цього проміжку відповідає більше значення функції, тобто якщо називають зростаючою на деякому проміжку Х, якщо більшому значенню аргументу з цього проміжку відповідає більше значення функції, тобто якщо 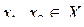 і і 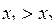 , то , то 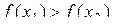 .
Функцію .
Функцію 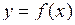 називають спадаючою на деякому проміжку Х, якщо більшому значенню аргументу з цього проміжку відповідає менше значення функції, тобто якщо називають спадаючою на деякому проміжку Х, якщо більшому значенню аргументу з цього проміжку відповідає менше значення функції, тобто якщо 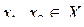 і і 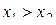 , то , то 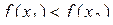 .
Зростаючі і спадаючі функції називають монотонними. .
Зростаючі і спадаючі функції називають монотонними.
|
|
|
|
Функцію 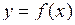 називають періодичною з періодом Т, якщо для будь-якого значення х, при якому вона визначена, тобто при називають періодичною з періодом Т, якщо для будь-якого значення х, при якому вона визначена, тобто при 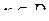 , виконується рівність , виконується рівність 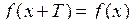 , причому , причому 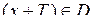 . .
|
Нехай 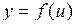 , , 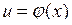 , тоді функцію , тоді функцію 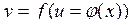 називають складною, а u називають проміжним аргументом. називають складною, а u називають проміжним аргументом.
|
Основними елементарнимифункціями є:
Степенева функція 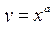 .
.
Для будь-якого а область визначення 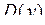 функції містить додатну піввісь
функції містить додатну піввісь 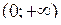 . Точка
. Точка  включається в область визначення при
включається в область визначення при 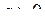 і виключається при
і виключається при 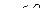 . Від’ємна піввісь
. Від’ємна піввісь 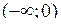 міститься в області визначення в окремих випадках (наприклад, при
міститься в області визначення в окремих випадках (наприклад, при 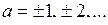 ;
; 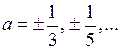 ).
).
Показникова функція 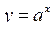 (
( 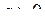 ,
,  ).
).
Область визначення функції  .
.
Логарифмічна функція 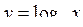 (
(  ,
,  ).
).
Область визначення функції 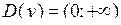 .
.
Тригонометричні функції 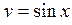 ,
, 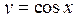 .
.
Функції 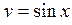 ,
, 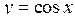 мають область визначення
мають область визначення 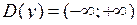 .
.
Обернені тригонометричні функції 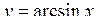 ,
, 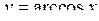 ,
, 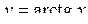 ,
, 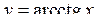 .
.
Областю визначення функцій 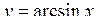 ,
, 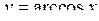 є
є 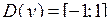 , а областю визначення функцій
, а областю визначення функцій 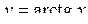 ,
, 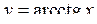 є
є 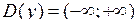
Дата добавления: 2019-02-13; просмотров: 160; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
