Основні властивості векторного добутку векторів
| 1) | 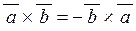 ; ;
|
| 2) | 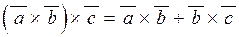 ; ;
|
| 3) | 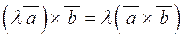 ; ;
|
| 4) | векторний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли вектори колінеарні:
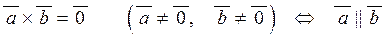 ; ;
|
| 5) | 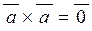 . .
|
| Приклад 2.5. | Знайти синус кута між векторами 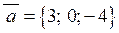 i i  , а також площу паралелограма, побудованого на цих векторах. , а також площу паралелограма, побудованого на цих векторах.
|
Розв’язання. За формулою (2.11) обчислимо векторний добуток 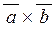 :
:
 .
.
Довжину векторів 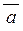 ,
,  і
і 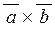 знайдемо згідно (2.3):
знайдемо згідно (2.3):
 ,
, 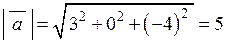 ,
, 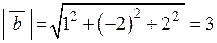 .
.
З формули (2.11) маємо: 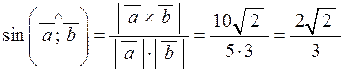 .
.
Відповідно до означення векторного добутку площа паралелограма, побудованого на векторах 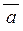 і
і 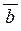 дорівнює
дорівнює 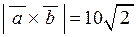 .
.
Мішаний добуток векторів
Мішаним добуткомвекторів 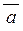 , , 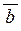 і і 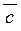 називається скалярний добуток вектора називається скалярний добуток вектора 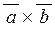 на вектор на вектор 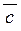 . .
|
Якщо 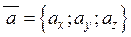 ,
, 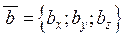 і
і 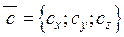 , то мішаний добуток векторів у координатній формі має вигляд:
, то мішаний добуток векторів у координатній формі має вигляд:
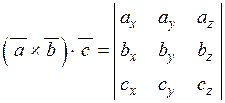 . (2.12)
. (2.12)
Основні властивості мішаного добутку векторів
| 1) | 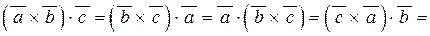
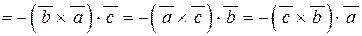 ; ;
|
| 2) | мішаний добуток трьох ненульових векторів дорівнює нулю тоді і тільки тоді, коли вони компланарні; |
| 3) | модуль мішаного добутку дорівнює об’єму паралелепіпеда, що побудовано на даних векторах; |
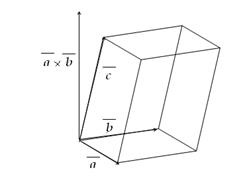
Рисунок 2.11 - Паралелепіпед, що побудовано на векторах  ,
,  і
і 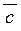 .
.
| Зауваження | Об’єм піраміди, яку побудовано на векторах 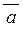 , , 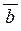 і і 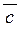 , дорівнює модулю змішаного добутку цих векторів, що поділено на 6. , дорівнює модулю змішаного добутку цих векторів, що поділено на 6.
|
| Приклад 2.6. | Довести, що точки 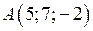 , ,  , , 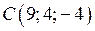 і і 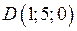 лежать в одній площині. лежать в одній площині.
|
Розв’язання. Знайдемо координати векторів, що виходять з точки  :
: 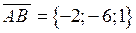 ,
, 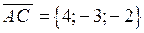 ,
, 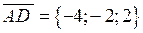 .
.
|
|
|
Доведемо, що ці вектори є компланарними, тобто належать одній площині. Для цього обчислимо мішаний добуток одержаних векторів:
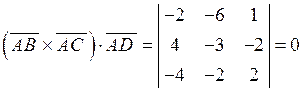 .
.
Згідно другої властивості мішаного добутку вектори 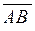 ,
, 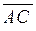 і
і  є компланарними, отже точки
є компланарними, отже точки  ,
,  ,
, 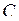 і
і 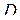 лежать в одній площині.
лежать в одній площині.
| Приклад 2.7. | Знайти об’єм піраміди 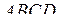 і довжину висоти і довжину висоти  , яку опущено на грань , яку опущено на грань  , якщо вершини , якщо вершини  , ,  , , 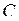 і і  мають наступні координати: мають наступні координати: 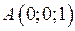 , , 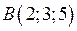 , , 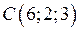 , , 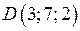 . .
|
Розв’язання. Знайдемо координати векторів, що виходять з вершини 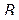 :
:  ,
, 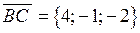 ,
,  .
.

Рисунок 2.12 - Піраміда, що побудована на векторах 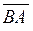 ,
, 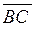 ,
, 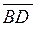 .
.
Обчислимо мішаний добуток одержаних векторів: 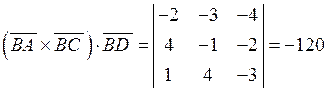 . Отже, об’єм піраміди
. Отже, об’єм піраміди 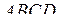 :
:
 .
.
Для знаходження висоти  обчислимо спочатку площу грані
обчислимо спочатку площу грані  , як модуля векторного добутку векторів
, як модуля векторного добутку векторів 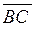 і
і 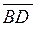 :
:
 ,
,
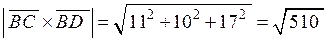 .
.
Отже, площа трикутника  дорівнює
дорівнює 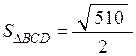 . Тоді з відомої формули
. Тоді з відомої формули 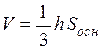 маємо
маємо 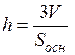 , звідки одержимо
, звідки одержимо  .
.
Пряма на площині
Розглянемо найпростішу лінію на площині – пряму. Існують різні форми запису рівняння прямої лінії на площині.
Нехай  − пряма лінія на координатній площині.
− пряма лінія на координатній площині. 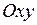 ,
, 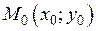 − фіксована точка на
− фіксована точка на  ,
, 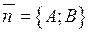 - ненульовий вектор
- ненульовий вектор  , перпендикулярний до
, перпендикулярний до 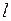 . Його називають нормальним вектором прямої.
. Його називають нормальним вектором прямої.
Завдання точки 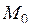 і вектора
і вектора  повністю визначає пряму
повністю визначає пряму 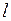 і таким чином можна задати будь-яку пряму лінію на площині. Довільна точка
і таким чином можна задати будь-яку пряму лінію на площині. Довільна точка 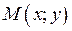 буде належати прямій
буде належати прямій 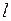 тоді і тільки тоді, коли вектори
тоді і тільки тоді, коли вектори 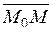 і
і  будуть взаємно перпендикулярними (рис. 2.13).
будуть взаємно перпендикулярними (рис. 2.13).
|
|
|

Рисунок 2.13 - Завдання прямої на площині.
Для цього, в свою чергу, необхідно і достатньо, щоб скалярний добуток цих векторів дорівнював нулю
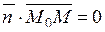 . (2.13)
. (2.13)
Оскільки  , то можна виразити скалярний добуток
, то можна виразити скалярний добуток 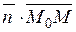 через координати множників:
через координати множників:
 . (2.14)
. (2.14)
Рівняння (2.14) є рівнянням прямої на площині в координатній формі. Відношення (2.14) називають ще рівнянням прямої, що проходить через задану точку в заданому напрямку.
Відношення
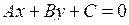 , (2.15)
де , (2.15)
де  , визначає загальне рівняння прямої на площині. , визначає загальне рівняння прямої на площині.
|
Термін «загальне» пояснюють тим, що довільна пряма на площині може бути заданою рівнянням першого степеня відносно змінних 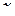 і
і  (при цьому коефіцієнти
(при цьому коефіцієнти 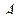 і
і 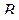 не дорівнюють нулю одночасно, бо нормальний вектор прямої не нульовий).
не дорівнюють нулю одночасно, бо нормальний вектор прямої не нульовий).
Пряма лінія на площині – це геометричне місце точок площини, координати яких задовольняють рівнянню першої степені відносно 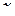 і і  . .
|
Будь-яка пряма на площині визначається рівнянням першого ступеня відносно 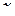 і
і  . Будь-якому рівнянню першого ступеня відносно
. Будь-якому рівнянню першого ступеня відносно 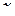 і
і  відповідає пряма лінія в декартовій системі координат
відповідає пряма лінія в декартовій системі координат 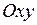 .
.
|
|
|
Відмітимо характерні випадки загального рівняння прямої, коли деякі коефіцієнти дорівнюють нулю.
| 1) | Нехай  , тоді рівняння (2.15) має вигляд: , тоді рівняння (2.15) має вигляд:
 де
де 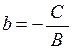 . Всі точки прямої мають однакову ординату, тобто пряма паралельна осі абсцис . Всі точки прямої мають однакову ординату, тобто пряма паралельна осі абсцис 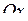 . .
|
| 2) | Нехай  , тоді , тоді  . Пряма співпадає з віссю . Пряма співпадає з віссю 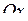 . .
|
| 3) | Нехай 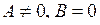 , тоді рівняння (2.15) має вигляд: , тоді рівняння (2.15) має вигляд:
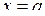 ,
де ,
де 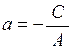 . Всі точки прямої мають однакову абсцису, тому пряма паралельна осі ординат . Всі точки прямої мають однакову абсцису, тому пряма паралельна осі ординат 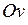 . .
|
| 4) | Нехай 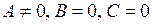 , тоді , тоді 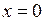 . Пряма співпадає з віссю . Пряма співпадає з віссю 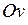 . .
|
| 5) | Нехай 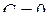 , тоді пряма , тоді пряма  незалежно від значень незалежно від значень 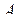 і і 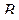 проходить через початок координат т. проходить через початок координат т. 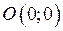 . .
|
Нехай 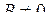 . Розв’яжемо рівняння (2.15) відносно змінної
. Розв’яжемо рівняння (2.15) відносно змінної  :
:
 ,
,
або
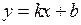 . (2.16)
. (2.16)
| Рівняння (2.16) називають рівнянням прямої з кутовим коефіцієнтом і початковою ординатою. |
Зміст коефіцієнтів у (2.16):

| 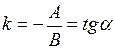 ‑ кутовий коефіцієнт прямої, ‑ кутовий коефіцієнт прямої, 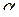 − кут нахилу прямої до − кут нахилу прямої до 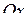 . .
|

| 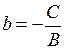 − ордината точки перетину прямої з віссю − ордината точки перетину прямої з віссю 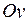 , початкова ордината прямої (рис. 2.14). , початкова ордината прямої (рис. 2.14).
|

Рисунок 2.14 - Пряма з кутовим коефіцієнтом
|
|
|
Рівняння
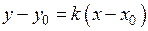 (2.17)
називають рівнянням прямої, яка проходить через задану точку в заданому напрямку. (2.17)
називають рівнянням прямої, яка проходить через задану точку в заданому напрямку.
|
При фіксованій точці  і різних значеннях
і різних значеннях  це рівняння дає множину прямих, яку називають пучком прямих з центром в точці
це рівняння дає множину прямих, яку називають пучком прямих з центром в точці 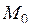 . Але тільки одну пряму з всіх, які проходять через
. Але тільки одну пряму з всіх, які проходять через  , а саме пряму, перпендикулярну до осі абсцис, не можна визначити таким рівнянням. Її рівнянням буде
, а саме пряму, перпендикулярну до осі абсцис, не можна визначити таким рівнянням. Її рівнянням буде  .
.
Нехай потрібно скласти рівняння прямої, що проходить через дві задані точки 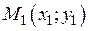 і
і 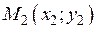 (вважаємо, що
(вважаємо, що 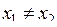 ,
, 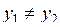 ).
).
Знайдемо кутовий коефіцієнт цієї прямої, для чого обчислимо тангенс кута, який утворює відрізок 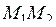 з віссю
з віссю 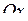 (рис.2.15)
(рис.2.15)
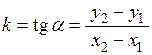 . (2.18)
. (2.18)
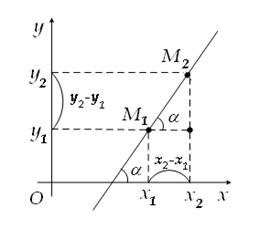
Рисунок 2.15 - Рівняння прямої, що проходить через дві задані точки
Підставимо вираз (2.18) у відношення (2.17) і запишемо останнє рівняння в симетричній формі:
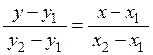 . (2.19)
. (2.19)
| Рівняння (2.19) називають рівнянням прямої, яка проходить через дві задані точки. |
Нехай пряма 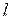 відсікає на осі абсцис відрізок
відсікає на осі абсцис відрізок 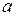 , а на осі ординат – відрізок
, а на осі ординат – відрізок 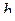 (рис. 2.16), тоді шукана пряма проходить через точки
(рис. 2.16), тоді шукана пряма проходить через точки 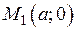 і
і 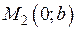 .
.
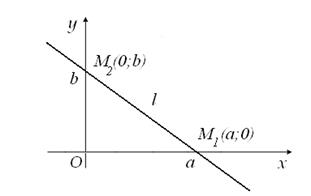
Рисунок 2.16. - Рівняння прямої у відрізках на осях
Підставимо координати цих точок у рівняння (2.19) і одержимо:
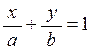 . (2.20)
. (2.20)
Рівняння (2.20) називають рівнянням прямої у відрізках на осях. Тут величини 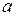 і і 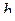 − це довжини, які взяли з належними знаками, відрізків, що пряма − це довжини, які взяли з належними знаками, відрізків, що пряма 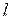 відсікає від осей координат. відсікає від осей координат.
|
Нехай прямі 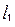 і
і  задано рівняннями:
задано рівняннями:
 ,
, 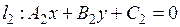 .
. 
Тоді вектор 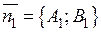 буде нормальним до
буде нормальним до  , а вектор
, а вектор 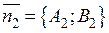 буде нормальним до
буде нормальним до  .
.
Якщо прямі 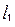 і
і  непаралельні, то кут
непаралельні, то кут 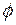 між нормальними векторами
між нормальними векторами  і
і  дорівнює одному з кутів, створених прямими
дорівнює одному з кутів, створених прямими  і
і  .
.
З формули (2.6) маємо:
 . (2.21)
. (2.21)
Якщо 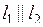 , то
, то 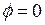 або
або 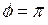 .
.
Часто зручнішою виявляється формула, яка пов’язує тангенс кута між двома прямими через їхні коефіцієнти  і
і 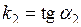 :
:
 (2.22)
(2.22)
| Приклад 2.8. | Знайти кут 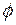 між прямими між прямими 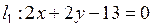 і і 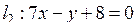 . .
|
Розв’язання. За формулою (2.21) одержимо:
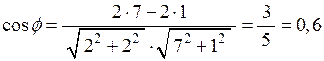 .
.
Отже, 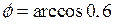 .
.
Дата добавления: 2019-02-13; просмотров: 287; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
