Границя послідовності та її властивості
Першу спробу створити теорію границь зробив Ньютон у 1686 р., хоча операція граничного переходу застосовувалася і раніше, починаючи із старогрецьких учених. Близьке до сучасного поняття границі сформулював у 1765 р. французький математик і філософ Ж. Даламбер.
Якщо кожному натуральному числу 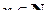 поставлене у відповідність деяке дійсне число хn, то говорять, що задано послідовність чисел х1, х2, …, хn, … Інші позначення: {хn}, хn.
поставлене у відповідність деяке дійсне число хn, то говорять, що задано послідовність чисел х1, х2, …, хn, … Інші позначення: {хn}, хn.
Числовою послідовністю 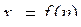 , (n = 1, 2,...) називають множину значень функції , (n = 1, 2,...) називають множину значень функції 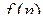 , яку визначено на множині натуральних чисел.
Числа х1, х2,… називають членами (елементами) послідовності, , яку визначено на множині натуральних чисел.
Числа х1, х2,… називають членами (елементами) послідовності, 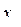 – загальним членом послідовності, n – номером члена послідовності. – загальним членом послідовності, n – номером члена послідовності.
|
Наприклад, розглянемо послідовність 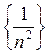 . Загальний член її ‑
. Загальний член її ‑ 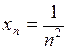 . Перші п’ять членів такі: х1= 1, х2 =
. Перші п’ять членів такі: х1= 1, х2 = 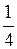 , х3 =
, х3 = 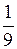 , х4 =
, х4 = 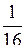 , х5 =
, х5 = 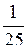 .
.
Наприклад, членами послідовності 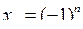 є числа
є числа 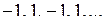
Прикладом послідовності є нескінченно спадаюча геометрична прогресія 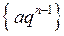 , де
, де 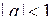 .
.
Число а називають границею послідовності {хn}, якщо для будь-якого наперед заданого (навіть скільки завгодно малого) числа  знайдеться такий номер знайдеться такий номер 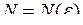 , що для всіх , що для всіх 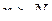 буде виконуватися нерівність буде виконуватися нерівність
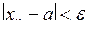 . (3.1) . (3.1)
|
Для позначення границі 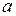 послідовності {хn} використовується запис:
послідовності {хn} використовується запис: 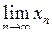 = а, або
= а, або 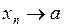 при
при 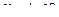 .
.
Інтервал виду 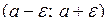 , де
, де 
 , називають e -окілом точки а.
, називають e -окілом точки а.
Геометрична інтерпретація границі послідовності. Якщо а – границя послідовності {хn}, то для будь-якого  (навіть скільки завгодно малого) можна знайти такий номер
(навіть скільки завгодно малого) можна знайти такий номер 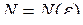 , що при
, що при 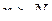 всі члени послідовності попадуть в e-окіл точки а. Інакше кажучи, для будь-якого околу з центром в точці а, навіть скільки завгодно малого радіусу e, знайдеться таке значення хn, що точки, що зображають ці значення, і всі подальші значення послідовності {хn}, потраплять в цей окіл (рис.3.1). Таким чином, зовні e-околу точки а може лежати лише скінчене число членів послідовності {хn}.
всі члени послідовності попадуть в e-окіл точки а. Інакше кажучи, для будь-якого околу з центром в точці а, навіть скільки завгодно малого радіусу e, знайдеться таке значення хn, що точки, що зображають ці значення, і всі подальші значення послідовності {хn}, потраплять в цей окіл (рис.3.1). Таким чином, зовні e-околу точки а може лежати лише скінчене число членів послідовності {хn}.
|
|
|

Рисунок 3.1 – Геометрична інтерпретація границі послідовності
| Послідовність називають збіжною, якщо вона має границю, якщо послідовність границі не має, то вона називається розбіжною. |
Послідовність може прямувати до своєї границі різними способами:
залишаючись менше своєї границі;
залишаючись більше своєї границі;
коливаючись біля своєї границі.
Числову послідовність називають зростаючою, якщо кожен наступний член послідовності більше попереднього, тобто 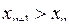 . .
|
Приклади зростаючих послідовностей: 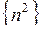 ,
, 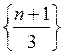 .
.
Числову послідовність називають спадаючою, якщо кожен наступний член послідовності менше попереднього, тобто 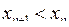 . .
|
|
|
|
Приклади спадаючих послідовностей: 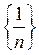 ,
, 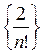 .
.
| Монотонними послідовностями називають зростаючі і спадаючі послідовності. |
Послідовність називають обмеженою, якщо існує число 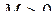 таке, що для всіх значень n = 1,2,... виконується нерівність таке, що для всіх значень n = 1,2,... виконується нерівність 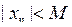 . .
|
Приклади обмежених послідовностей: 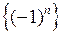 ,
, 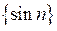 ,
, 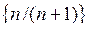 ; необмежених послідовностей:
; необмежених послідовностей: 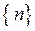 ,
, 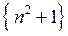 ,
, 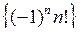 .
.
Дата добавления: 2019-02-13; просмотров: 166; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
