Властивості нескінченно великих послідовностей
| 1) | Сума нескінченно великої послідовності і обмеженої є нескінченно великою послідовністю. | |
| 2) | Сума нескінченно великих послідовностей однакового знаку є нескінченно великою послідовністю. | |
| 3) | Добуток нескінченно великих послідовностей є нескінченно великою послідовністю. | |
| 4) | Добуток нескінченно великої послідовності на постійну величину, що не дорівнює нулю, є нескінченно великою послідовністю. | |
| Зауваження. | Відношення двох нескінченно великих величин може бути величиною скінченою, нескінченно малою і нескінченно великою. Відношення двох нескінченно великих величин є “невизначеністю” виду 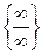 . .
| |
Зв’язок між нескінченно великими і нескінченно малими послідовностями
| Теорема 3.11. | Якщо {xn} – нескінченно мала послідовність, то 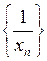 – нескінченно велика послідовність. І навпаки, якщо {yn} – нескінченно велика послідовність, то – нескінченно велика послідовність. І навпаки, якщо {yn} – нескінченно велика послідовність, то 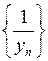 – нескінченно мала послідовність. – нескінченно мала послідовність.
|
Границя функції та її властивості
Розглянемо функцію 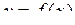 , визначену на деякому проміжку
, визначену на деякому проміжку 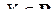 . Нехай аргумент х приймає послідовність значень х1, х2,…, хn,…, де
. Нехай аргумент х приймає послідовність значень х1, х2,…, хn,…, де 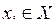 . Відповідні значення функції утворюють послідовність у1, у2,…, уn,..., де
. Відповідні значення функції утворюють послідовність у1, у2,…, уn,..., де 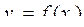 .
.
Означення границі функції за Гейне:
Число А називають границею функції 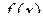 при при 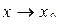 (або в точці х0), якщо для довільної послідовності {xn}, що збігається до х0,відповідна послідовність значень функції {yn} збігається до А. (або в точці х0), якщо для довільної послідовності {xn}, що збігається до х0,відповідна послідовність значень функції {yn} збігається до А.
|
|
|
|
Позначення: 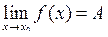 , або
, або 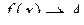 при
при 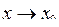 .
.
Означення границі функції за Коші:
Число А називають границею функції 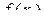 при х, що прямує до х0, якщо для будь-якого (навіть скільки завгодно малого) при х, що прямує до х0, якщо для будь-якого (навіть скільки завгодно малого)  можна знайти таке число можна знайти таке число 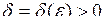 , що як тільки , що як тільки 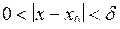 , то виконується нерівність , то виконується нерівність
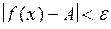 . (3.2) . (3.2)
|
Означення границі функції за Гейне і за Коші є еквівалентними.
Геометрична інтерпретація границі функції за Коші
Нехай дано графік функції 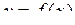 , яка має границю, що дорівнює числу А при
, яка має границю, що дорівнює числу А при  (рис.3.1.1). Для будь-якого наперед заданого додатного числа
(рис.3.1.1). Для будь-якого наперед заданого додатного числа  знайдеться окіл точки а радіусу
знайдеться окіл точки а радіусу 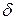 такий, що частина графіка функції
такий, що частина графіка функції 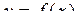 , що відповідає околу (а –d, а + d), міститься усередині смуги, обмеженої прямими у = А –e, у = А +e. Відзначимо, що в точці а функція
, що відповідає околу (а –d, а + d), міститься усередині смуги, обмеженої прямими у = А –e, у = А +e. Відзначимо, що в точці а функція 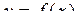 може приймати значення, яке не дорівнює А, або взагалі може бути не визначена.
може приймати значення, яке не дорівнює А, або взагалі може бути не визначена.
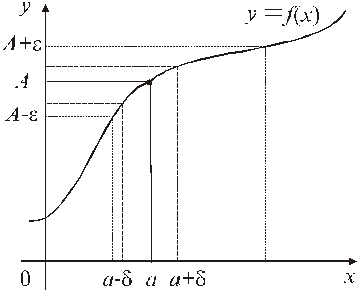
Рисунок 3.2 – Геометрична інтерпретація границі функції
| Теорема 3.12. | Якщо функція 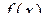 має границю має границю 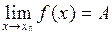 , то вона (границя) є єдиною. , то вона (границя) є єдиною.
|
Теорема 3.12 виходить з теореми 3.1, оскільки послідовність, що збігається, може мати тільки одну границю.
| Приклад 3.4. | Довести, що 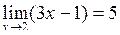 . .
|
Розв’язання. Візьмемо яке-небудь число  . Завдання полягає в тому, що за заданим числом
. Завдання полягає в тому, що за заданим числом 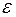 знайти таке
знайти таке 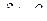 , для якого з нерівності
, для якого з нерівності
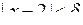 випливала б нерівність
випливала б нерівність 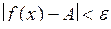 або
або 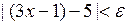 .
.
|
|
|
Після перетворення останньої нерівності, отримаємо
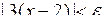 або
або 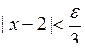 .
.
Таким чином, якщо узяти 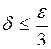 , то для всіх х, що задовольняють нерівність
, то для всіх х, що задовольняють нерівність 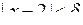 буде виконуватися нерівність
буде виконуватися нерівність 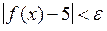 . Це означає, що
. Це означає, що 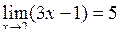 .
.
Наприклад, якщо 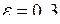 , то
, то 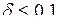 ; якщо
; якщо 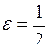 , то
, то 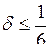 , і т.д.
, і т.д.
| Теорема 3.13. | (ознака існування границі функції) Якщо в деякому околі точки а для трьох функцій виконується нерівність 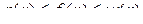 , і , і 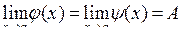 , то , то 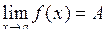 . .
|
Дата добавления: 2019-02-13; просмотров: 471; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
