Границя функції на нескінченності і нескінченні границі
Число А називають границею функції 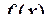 при при 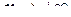 , якщо для будь-якого , якщо для будь-якого  можна знайти число можна знайти число 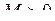 таке, що при таке, що при 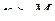 , виконується нерівність , виконується нерівність 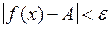 . Позначення: . Позначення: 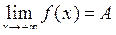 . .
|
Число А називають границею функції 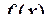 при при 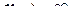 , якщо для будь-якого , якщо для будь-якого  можна знайти число можна знайти число 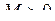 таке, що при таке, що при 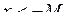 , виконується нерівність , виконується нерівність 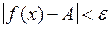 . Позначення: . Позначення: 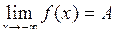 . .
|
Число А називають границею функції 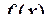 при при 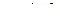 , якщо для будь-якого , якщо для будь-якого  можна знайти число можна знайти число 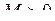 таке, що при таке, що при 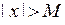 , виконується нерівність , виконується нерівність 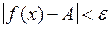 . Позначення: . Позначення: 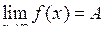 . .
|
Функція 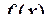 має своєю границею має своєю границею 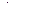 при при  , якщо для будь-якого , якщо для будь-якого 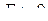 можна знайти число можна знайти число 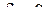 таке, що при всіх таке, що при всіх  , що задовольняють нерівності , що задовольняють нерівності 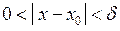 , буде виконуватися нерівність , буде виконуватися нерівність 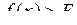 . Позначення: . Позначення: 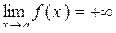 . .
|
Функція 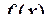 має своєю границею має своєю границею  при при  ,якщо для будь-якого ,якщо для будь-якого  можна знайти число можна знайти число  таке, що при всіх таке, що при всіх  , що задовольняють нерівності , що задовольняють нерівності 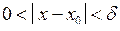 , буде виконуватися нерівність , буде виконуватися нерівність 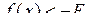 . Позначення: . Позначення: 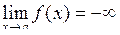 . .
|
Функція 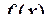 має своєю границею має своєю границею 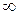 при при  , якщо для будь-якого , якщо для будь-якого 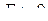 можна знайти число можна знайти число 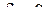 таке, що при всіх таке, що при всіх  , що задовольняють нерівності , що задовольняють нерівності 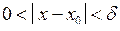 , буде виконуватися нерівність , буде виконуватися нерівність 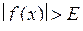 . Позначення: . Позначення: 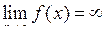 . .
|
Односторонні границі функції
Лівобічною границею функції 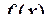 називають число А1при називають число А1при 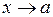 , за умови, що x, починаючи з деякого моменту прийматиме значення, які менші за а. Використовують позначення , за умови, що x, починаючи з деякого моменту прийматиме значення, які менші за а. Використовують позначення 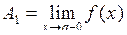 або або 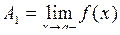 . .
|
Правобічною границею функції 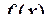 називають число А2при називають число А2при 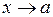 , за умови, що x, починаючи з деякого моменту прийматиме значення, які більші за а. Використовують позначення , за умови, що x, починаючи з деякого моменту прийматиме значення, які більші за а. Використовують позначення 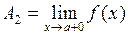 або або 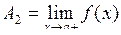 . .
|
| Приклад 3.5. | Знайти лівобічну і правобічну границі функції
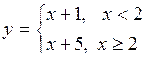 при x ® 2. при x ® 2.
|
|
|
|
Розв’язання. В даному випадку значення границі залежить від того, з якого боку x прямувати до 2. Якщо x прямує до 2 зліва, тобто з боку значень, менших за 2 (  ), то застосовуємо вираз
), то застосовуємо вираз  і
і 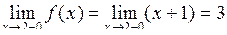 .
.
Якщо x прямує до 2 праворуч, тобто з боку значень, більших за 2, ( 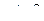 ), то застосовуємо вираз
), то застосовуємо вираз 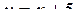 , і
, і 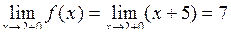 .
.
Функцію 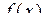 називають нескінченно малою при х®а, якщо називають нескінченно малою при х®а, якщо 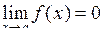 . .
|
Функцію 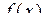 називають нескінченно великою при х®а, якщо називають нескінченно великою при х®а, якщо 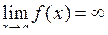 . .
|
Властивості нескінченно малих і нескінченно великих послідовностей притаманні також і нескінченно малим і нескінченно великим функціям.
Обчислення границь
Методи розкриття невизначеностей
Під час обчислення границь функції 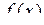 доводиться зустрічатися з двома різними типами прикладів.
доводиться зустрічатися з двома різними типами прикладів.
Функція 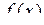 визначена в граничній точці
визначена в граничній точці 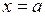 . Тоді
. Тоді 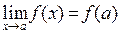 .
.
| Приклад 4.1. | Знайти 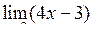 . .
|
Розв’язання. Для знаходження границі цілої раціональної функції 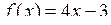 потрібно замінити змінну
потрібно замінити змінну  її граничним значенням, тобто
її граничним значенням, тобто
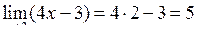 .
.
Функція 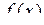 у граничній точці
у граничній точці 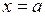 не визначена або треба обчислити границю функції при
не визначена або треба обчислити границю функції при  .
.
Тоді обчислення границі в кожному окремому випадку вимагає індивідуального підходу. В одних випадках питання зводиться безпосередньо до застосування теорем про властивості нескінченно малих, в інших – функція 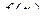 у точці
у точці 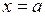 або при
або при  є невизначеністю, тобто виразом вигляду
є невизначеністю, тобто виразом вигляду 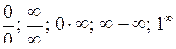 та ін.
та ін.
|
|
|
| 1. | Невизначеність 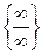 розкривають діленням чисельника і знаменника на найбільший степінь аргументу. розкривають діленням чисельника і знаменника на найбільший степінь аргументу.
|
| Приклад 4.2. | Знайти 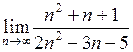 . .
|
Розв’язання. Чисельник і знаменник дробу розділимо на 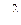 :
:
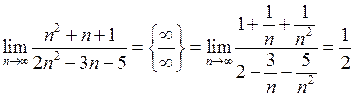 .
.
| Приклад 4.3. | Знайти 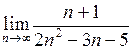 . .
|
Розв’язання. Чисельник і знаменник дробу розділимо на 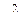 :
:
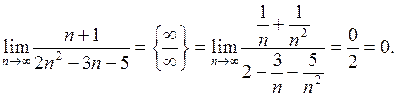
| Приклад 4.4. | Знайти 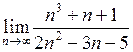 . .
|
Розв’язання. Чисельник і знаменник дробу розділимо на 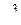 :
:
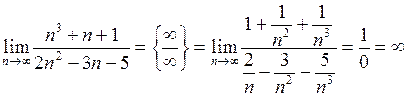 .
.
Щоб розкрити невизначеність 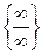 , що отримана відношенням двох многочленів, можна скористатися наступним правилом:
, що отримана відношенням двох многочленів, можна скористатися наступним правилом:
якщо старший степінь чисельника більше старшого степеня знаменника, то границя відношення дорівнює нескінченності.
якщо старший степінь чисельника дорівнює старшому степеню знаменника, то границя відношення дорівнює відношенню коефіцієнтів при старших степенях многочленів.
якщо старший степінь чисельника менше старшого степеня знаменника, границя відношення дорівнює нулю.
|
|
|
| Приклад 4.5. | Знайти 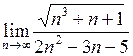 . .
|
Розв’язання. Старший степінь чисельника 3/2, а знаменника – 2. За вищезгаданим правилом маємо: 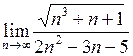 = 0.
= 0.
| 2. | Невизначеність {µ – µ} розкривають приведенням до спільного знаменника дробів або позбавленням від ірраціональності в чисельнику. |
| Приклад 4.6. | Знайти 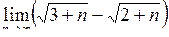 . .
|
Розв’язання. Помножимо і розділимо вираз, що стоїть під знаком границі, на спряжений вираз 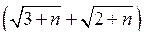 :
:
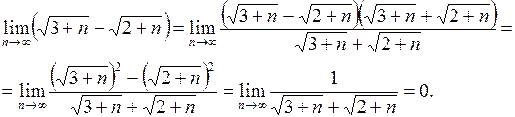
| Приклад 4.7. | Знайти 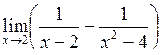 . .
|
Розв’язання. Приведемо дроби до спільного знаменника, тоді
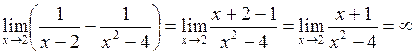 .
.
| 3. | Невизначеність 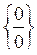 у разі, коли в чисельнику і знаменнику дробу є многочлени, розкривають шляхом розкладання чисельника і знаменника на множники і скороченням на спільний множник. у разі, коли в чисельнику і знаменнику дробу є многочлени, розкривають шляхом розкладання чисельника і знаменника на множники і скороченням на спільний множник.
|
| Приклад 4.8. | Знайти 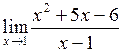 . .
|
Розв’язання. Маємо невизначеність 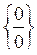 . Розкладемо чисельник на множники і скоротимо:
. Розкладемо чисельник на множники і скоротимо:
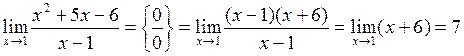 .
.
| Приклад 4.9. | Знайти 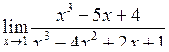 . .
|
Розв’язання. В даному випадку при  чисельник і знаменник дробу дорівнюють нулю. Маємо невизначеність
чисельник і знаменник дробу дорівнюють нулю. Маємо невизначеність 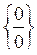 . Розділимо многочлен, що стоїть в чисельнику, на
. Розділимо многочлен, що стоїть в чисельнику, на  в стовпчик (під кутом):
в стовпчик (під кутом):
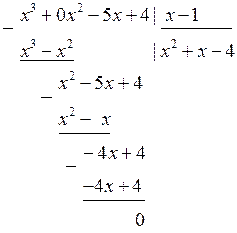
Розділимо многочлен, що стоїть в знаменнику, на  в стовпчик:
в стовпчик:
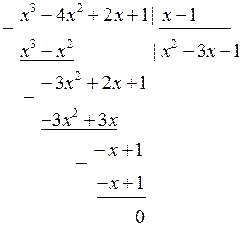
Таким чином, маємо:
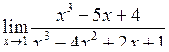
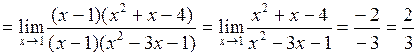 .
.
| Зауваження. | Ділення в стовпчик (під кутом) називають діленням за алгоритмом Евкліда. |
|
|
|
| 4. | Невизначеність 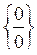 у разі, коли в чисельнику або знаменнику дробу (або і в чисельнику, і в знаменнику) є ірраціональності, розкривають шляхом перенесення ірраціональності в іншу частину дробу. у разі, коли в чисельнику або знаменнику дробу (або і в чисельнику, і в знаменнику) є ірраціональності, розкривають шляхом перенесення ірраціональності в іншу частину дробу.
|
| Приклад 4.10. | Знайти 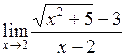 . .
|
Розв’язання. Маємо невизначеність 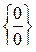 . Перенесемо ірраціональність з чисельника в знаменник, шляхом множення чисельника і знаменника дробу на спряжений вираз вигляду
. Перенесемо ірраціональність з чисельника в знаменник, шляхом множення чисельника і знаменника дробу на спряжений вираз вигляду 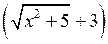 :
:
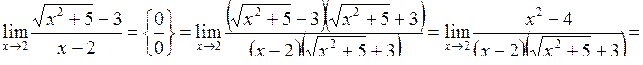
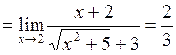 .
.
| Приклад 4.11. | Знайти 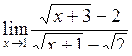 . .
|
Розв’язання. Маємо невизначеність 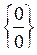 . Перенесемо ірраціональність з чисельника в знаменник і із знаменника в чисельник, шляхом множення чисельника і знаменника дробу на відповідні спряжені вирази:
. Перенесемо ірраціональність з чисельника в знаменник і із знаменника в чисельник, шляхом множення чисельника і знаменника дробу на відповідні спряжені вирази:
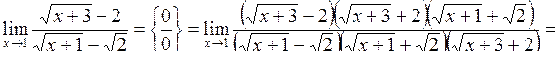
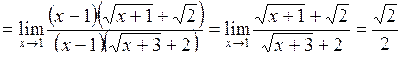 .
.
Визначні границі
При обчисленні границь тригонометричних виразів часто використовують формулу:
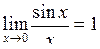 . (4.1)
. (4.1)
Формулу (4.1) називають першою визначною границею і застосовують для розкриття невизначеностей вигляду 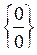 у разі коли функція, що стоїть під знаком границі, містить тригонометричні функції.
у разі коли функція, що стоїть під знаком границі, містить тригонометричні функції.
Справедливі наступні співвідношення:
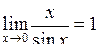 ,
, 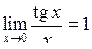 ,
, 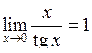 . (4.2)
. (4.2)
| Приклад 4.12. | Знайти 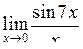 . .
|
Розв’язання. При х 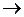 0 вираз
0 вираз 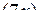 також прямує до нуля, тому, помноживши чисельник і знаменник на 7, отримаємо:
також прямує до нуля, тому, помноживши чисельник і знаменник на 7, отримаємо:
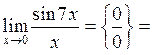
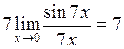 .
.
| Приклад 4.13. | Знайти 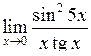 . .
|
Розв’язання. При х 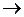 0 маємо невизначеність
0 маємо невизначеність 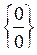 . Тому, враховуючи, що
. Тому, враховуючи, що 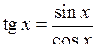 , та помножуючи чисельник і знаменник на 25х, отримаємо:
, та помножуючи чисельник і знаменник на 25х, отримаємо:
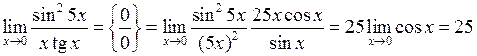 .
.
| Приклад 4.14. | Знайти 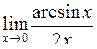 . .
|
Розв’язання. При х  0 маємо невизначеність вигляду
0 маємо невизначеність вигляду 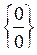 , тому, вводячи нову змінну у, отримаємо
, тому, вводячи нову змінну у, отримаємо
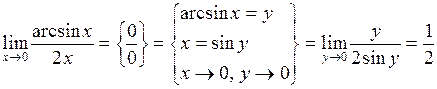
| Приклад 4.15. | Знайти 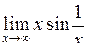 . .
|
Розв’язання. 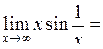
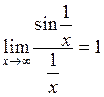 за формулою (4.1), оскільки
за формулою (4.1), оскільки 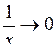 при
при  .
.
Границею функції 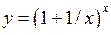 при
при 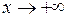 називають число e. Воно ірраціональне. Приблизне значення
називають число e. Воно ірраціональне. Приблизне значення 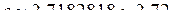 . Маємо:
. Маємо:
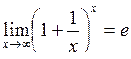 . (4.3)
. (4.3)
Позначення цієї границі через e прийняте на знак пошани до Ейлера. Число e має велике значення в математичному аналізі і його застосуваннях. Співвідношення (4.3) називають другою визначною границею. Співвідношення (4.3) можна записати у вигляді:
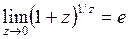 . (4.4)
. (4.4)
Другу визначну границю застосовують при розкритті невизначеності 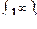 .
.
| Приклад 4.16. | Знайти 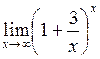 . .
|
Розв’язання. При х 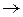
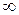 маємо невизначеність
маємо невизначеність 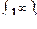 тому, перетворюючи вираз, що стоїть під знаком границі до вигляду (4.3), отримаємо:
тому, перетворюючи вираз, що стоїть під знаком границі до вигляду (4.3), отримаємо:
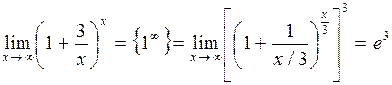 .
.
| Приклад 4.17. | Знайти 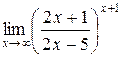 . .
|
Розв’язання. При х 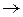
 маємо невизначеність
маємо невизначеність 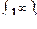 тому, виділивши цілу частину в функції, що стоїть під знаком границі, за допомогою (4.4) отримаємо:
тому, виділивши цілу частину в функції, що стоїть під знаком границі, за допомогою (4.4) отримаємо:
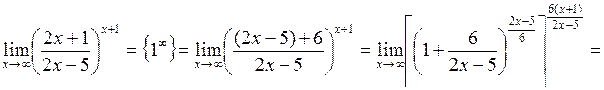
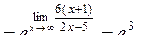
| Приклад 4.18. | Знайти 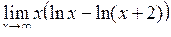 . .
|
Розв’язання. Спочатку перетворимо вираз, що стоїть під знаком границі, використовуючи властивості логарифмів, а потім скористаємось (4.4):
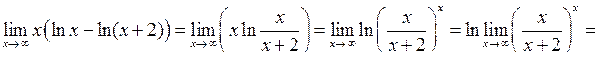
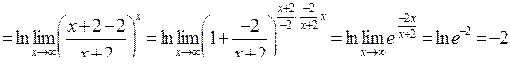 .
.
| Приклад 4.19. | Знайти 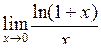 . .
|
Розв’язання. Виконавши перетворення з використанням властивостей логарифмів, за допомогою (4.3) отримаємо:
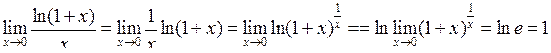 .
.
| Приклад 4.20. | Знайти 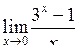 . .
|
Розв’язання. Перейшовши до нової змінної, за допомогою (4.3) отримаємо:
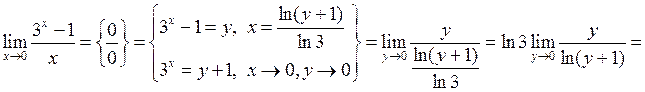
 .
.
Дата добавления: 2019-02-13; просмотров: 370; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
