Похідні функцій, заданих у параметричній, неявній формах, логарифмічне диференціювання
Розглянемо функцію, задану параметрично:
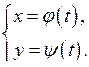
Нехай функції 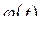 і
і 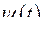 диференційовані і
диференційовані і 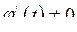 , тоді похідна
, тоді похідна  має вигляд:
має вигляд:
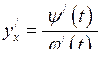 . (6.2)
. (6.2)
| Приклад 6.5. | Знайти похідну  функції, заданої параметрично функції, заданої параметрично 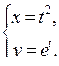 . .
|
Розв’язання. За формулою (6.2) маємо:
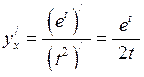 .
.
Нехай функцію 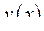 задано неявно відношенням:
задано неявно відношенням:
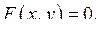
Для знаходження похідної 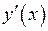 потрібно продиференціювати
потрібно продиференціювати 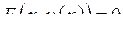 , вважаючи
, вважаючи 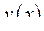 функцією аргументу
функцією аргументу  .
.
| Приклад 6.6. | Знайти похідну 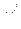 функції функції 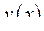 , яку задано неявно відношенням , яку задано неявно відношенням 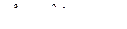
|
Розв’язання. Продиференціюємо рівняння, що задає функцію 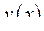 :
:
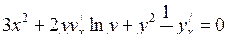 .
.
Винесемо 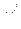 за дужки:
за дужки:
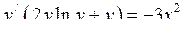 ,
,
Тоді похідна
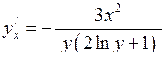 .
.
Нехай функцію 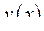 задано у вигляді
задано у вигляді 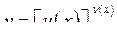 для знаходження похідної
для знаходження похідної 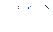 доцільно провести попереднє логарифмування функції, а потім знайти похідну неявної функції:
доцільно провести попереднє логарифмування функції, а потім знайти похідну неявної функції:
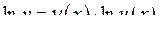 ,
,
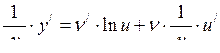 ,
,
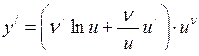 .
.
Це формула логарифмічного диференціювання.
| Приклад 6.7. | Знайти похідну функції  . .
|
Розв’язання. Прологарифмуємо рівність: 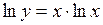 та визначимо похідну неявної функції
та визначимо похідну неявної функції 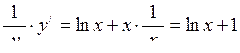 .
.
Тоді 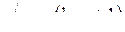 , тобто
, тобто 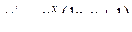 .
.
| Зауваження. | Логарифмічне диференціювання застосовують, коли функція є добутком багатьох множників. |
| Приклад 6.8. | Знайти похідну функції 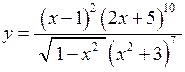 . .
|
Розв’язання. Знайдемо логарифм функції 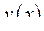 :
:
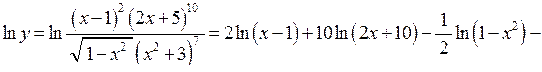
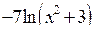 .
.
Визначимо похідну отриманої неявної функції:
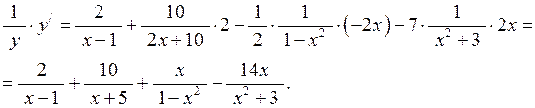
Отже, 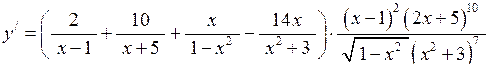 .
.
Диференціал функції однієї змінної
Нехай функція 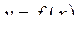 має похідну в точці
має похідну в точці  , тобто існує границя (6.1). Тоді (6.1) можна записати наступним чином:
, тобто існує границя (6.1). Тоді (6.1) можна записати наступним чином:
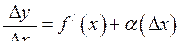 , (6.3)
, (6.3)
|
|
|
де 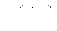 – нескінченно мала величина, тобто
– нескінченно мала величина, тобто 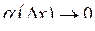 при
при 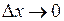 .
.
З відношення (6.3) випливає, що приріст функції 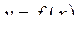 у точці
у точці  можна записати у вигляді:
можна записати у вигляді:
 . (6.4)
. (6.4)
Диференціалом функції 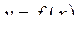 в точці в точці  називають головну лінійну частину приросту функції. Його позначають називають головну лінійну частину приросту функції. Його позначають
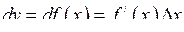 . (6.5) . (6.5)
|
| Приклад 6.9. | Знайти диференціал функції 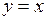 . .
|
Розв’язання. З формули (6.5) маємо: 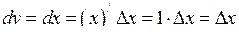 .
.
Отже, доведено рівність
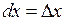 . (6.6)
. (6.6)
За допомогою відношення (6.6) рівняння (6.5) стає таким:
 . (6.7)
. (6.7)
Форма запису (6.7) диференціала функції дозволяє представити похідну як відношення диференціала функції до диференціала аргументу:
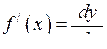 . (6.8)
. (6.8)
Геометричний зміст диференціала
Побудуємо на площині  графік функції
графік функції  . В точці
. В точці 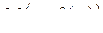 проведемо дотичну
проведемо дотичну 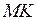 до графіка функції (рис. 6.6).
до графіка функції (рис. 6.6).
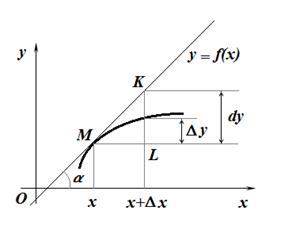
Рисунок 6.6 – Ілюстрація геометричного змісту диференціала
З трикутника 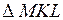 маємо:
маємо: 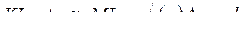 .
.
Таким чином, диференціал функції 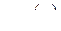 в точці
в точці  дорівнює приросту ординати дотичної до графіка цієї функції в точці
дорівнює приросту ординати дотичної до графіка цієї функції в точці 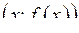 .
.
Нехай 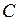 – стала величина,
– стала величина, 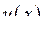 і
і 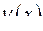 – диференційовані в точці
– диференційовані в точці  функції, тоді безпосередньо з визначення диференціала випливають наступні властивості.
функції, тоді безпосередньо з визначення диференціала випливають наступні властивості.
|
|
|
Властивості диференціала:
| 1) | 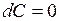 ; ;
|
| 2) | 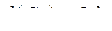 ; ;
|
| 3) | 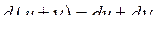 ; ;
|
| 4) | 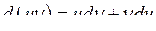 ; ;
|
| 5) | 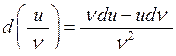  . .
|
Інваріантність форми диференціала першого порядку
Нехай 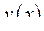 і
і 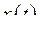 – диференційовані функції. Розглянемо диференціал складної функції
– диференційовані функції. Розглянемо диференціал складної функції 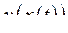 :
:
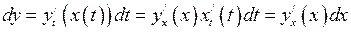 . (6.9)
. (6.9)
Формула (6.9) доводить цікавий факт: форма запису диференціала 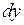 не залежить від того, чи буде
не залежить від того, чи буде  незалежною змінною або функцією іншої змінної.
незалежною змінною або функцією іншої змінної.
У зв’язку з цим цю властивість називають інваріантною формою запису диференціала.
| Приклад 6.9. | Знайти диференціали функцій  , ,  , , 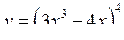 . .
|
Розв’язання. За визначенням диференціала маємо:
 ,
, 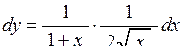 ,
, 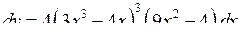 .
.
ДИФЕРЕНЦІЙОВАНІСТЬ ФУНКЦІЇ
БАГАТЬОХ ЗМІННИХ
Дата добавления: 2019-02-13; просмотров: 199; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
