Пример выполнения упражнения тренинга на компетенцию 7
Задание
Найдите уравнения касательной прямой и нормальной плоскости к винтовой линии: x = a cos t, y = a sin t, z = bt (a > 0, b > 0 – заданные константы) в точке M0, отвечающей значению  .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Определить значение параметра t0, соот-ветствующее заданной точке  на кривой на кривой
| Значение t0 дано по условию

|
| 2 | Если задано значение t0 параметра, то найти точку
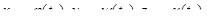
| Имеем:
 ; ; 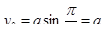 ; ;
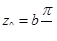 ; ; 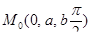
|
| 3 | Записать уравнение касательной прямой

| 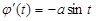 , ,  , ,
 , , 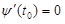 , ,
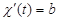 , ,  .
Поскольку .
Поскольку 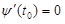 , то эту систему уравнений можно записать следующим образом: , то эту систему уравнений можно записать следующим образом:
 ; y – a = 0.
Таким образом, касательная лежит в
плоскости, параллельной, и имеет в этой плоскости уравнение. ; y – a = 0.
Таким образом, касательная лежит в
плоскости, параллельной, и имеет в этой плоскости уравнение.
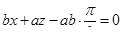
|
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 4 | Записать уравнение нормальной плос-кости:
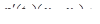 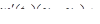
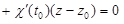
| 
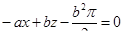 Отсутствие в получившемся уравнении озна-чает, что плоскость
Отсутствие в получившемся уравнении озна-чает, что плоскость 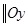 и стало быть перпен-дикулярна плоскостям, которые и стало быть перпен-дикулярна плоскостям, которые 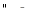 , а значит, и касательной прямой, как и должно было быть , а значит, и касательной прямой, как и должно было быть
|
Напишите самостоятельно уравнения:
7.1. Касательной прямой к линии:
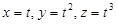 при t = 1.
при t = 1.
7.2. Нормальной плоскости к кривой из п.7.1 в точке, соответствующей t = –2.
Пример выполнения упражнения тренинга на компетенцию 8
Задание
Вычислите двойной интеграл 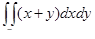 , где D – область, ограниченная кривыми y2 = 2x,
, где D – область, ограниченная кривыми y2 = 2x,
x + y = 4 и x = 8.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Нарисовать область интегрирования | Находим точки пересечения параболы и прямых:
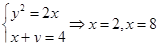 .
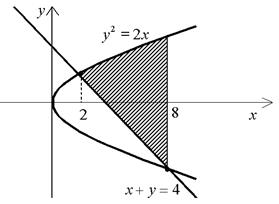
Область D имеет вид: .
Область D имеет вид:
|
| 2 | Представить двойной интеграл в виде повторного, определив порядок интег-рирования и расставив пределы интег-рирования | 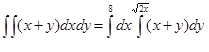
|
| 3 | Вычислить повторный интеграл | 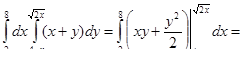
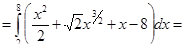
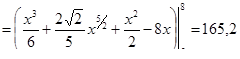
|
Вычислите самостоятельно двойные интегралы:
8.1. 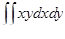 , где D – круг
, где D – круг 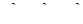 .
.
8.2. 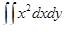 , где D – область, ограниченная прямыми y = x, y = –2 и x = 2.
, где D – область, ограниченная прямыми y = x, y = –2 и x = 2.
8.3. 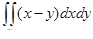 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 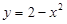 и y = –x.
и y = –x.
8.4. 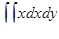 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями  и y = x – 2.
и y = x – 2.
8.5. 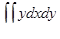 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 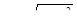 , y = x + 1 и x = 1.
, y = x + 1 и x = 1.
ГЛОССАРИЙ
| № п/п | Новое понятие | Содержание |
| 1 | 2 | 3 |
| 1 | Функция двух независимых переменных | если D – множество точек P плоскости xOy, определяемых двумя координатами x и y: P(x, y), то  – функция двух переменных – функция двух переменных
|
| 2 | Внутренняя точка | P – внутренняя точка для множества D, если существует s-окрестность P, целиком содержащаяся в D |
| 3 | Открытая область | такое множество, что: а) все ее точки внутренние; б) любые две точки P1 и P2 из D можно соединить непрерывной линией, лежащей в D |
| 4 | Граничная точка | точка P – граничная точка множества D, если в любой ее s-окрестности найдутся как точки из D, так и точки, не принадлежащие D |
| 5 | Замкнутая область | замкнутая область получается, если к открытой области присоединить все ее граничные точки |
| 6 | Линия уровня | если дана функция f(x, y), то линия уровня – это множество точек (x, y), для которых значения f(x, y) одинаковы: f(x, y) = C |
| 7 | Предел в точке для функции нескольких переменных | число a есть предел функции f(P) при  , если для , если для   такое, что во всех точках P области опреде-ления функции, попавших в s-окрестность точки P0, кроме, быть может, как в самой точке P0, выполняется неравенство: такое, что во всех точках P области опреде-ления функции, попавших в s-окрестность точки P0, кроме, быть может, как в самой точке P0, выполняется неравенство: 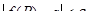 ; запись ; запись 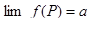
|
| 8 | Непрерывность функции двух переменных | функция f(P) непрерывна в точке P0, если
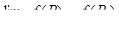 ; ; 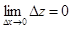
|
| 9 | Приращения функции двух переменных z = f( x, y) | 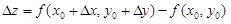 – полное – полное
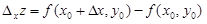 – частное по x – частное по x
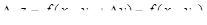 – частное по y – частное по y
|
| 10 | Частная производная | частная производная функции нескольких переменных по какой-то переменной – результат дифференцирования по этой переменной, при котором все остальные переменные считаются постоянными; в частности, для z = f(x, y) в точке (x0, y0):
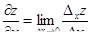 ; ; 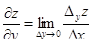
|
| 11 | Дифференцируемость функции двух переменных | функция z = f(x, y) дифференцируема в точке (x0, y0), если ее полное приращение можно представить формулой  , где , где 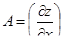 , , 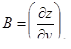 , o(r) –б.м. высшего порядка по сравнению с , o(r) –б.м. высшего порядка по сравнению с 
|
| 12 | Полный дифференциал функции двух переменных | главная часть полного приращения Dz, линейная относи-тельно Dx и Dy:
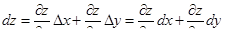
|
| 1 | 2 | 3 |
| 13 | Геометрический смысл полного дифференциала функции двух переменных | приращение аппликаты точки, двигающейся по касательной плоскости |
| 14 | Необходимый признак экстремума функции двух переменных | в точке экстремума частные производные равны нулю, если они существуют:
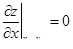 , , 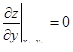
|
| 15 | Функция трех независимых переменных | 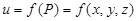 , если D – множество точек P трехмер-ного пространства, определяемых тремя координатами (x, y, z) , если D – множество точек P трехмер-ного пространства, определяемых тремя координатами (x, y, z)
|
| 16 | Поверхность уровня | для функции f(x, y, z) множество точек, в которых значения функции одинаковы f(x, y, z) = C |
| 17 | Пространство Rn | n-мерное пространство, точками P которого являются наборы из n чисел – координат точки P: 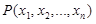 . Частные случаи: 1) R1 = R – числовая ось, точки P(x) обозначаются просто x; 2) R2 – плоскость, координаты точек обычно обозначаются x и y: P(x, y) или просто (x, y); 3) R3 – трехмерное (привычное) пространство, координаты точек обычно обозначаются x, y, z: P(x, y, z) или просто (x, y, z) . Частные случаи: 1) R1 = R – числовая ось, точки P(x) обозначаются просто x; 2) R2 – плоскость, координаты точек обычно обозначаются x и y: P(x, y) или просто (x, y); 3) R3 – трехмерное (привычное) пространство, координаты точек обычно обозначаются x, y, z: P(x, y, z) или просто (x, y, z)
|
| 18 | Расстояния в Rn | расстояние между 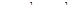 и и  вводится формулой вводится формулой 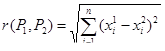
|
| 19 | s-окрестность точки P0 | множество всех точек P, для которых 
|
| 20 | Функция n независимых переменных | 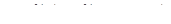 , если D – множество точек P n-мерного пространства, определяемых n координатами (x1, x2,…,xn): P(x1, x2,…,xn) , если D – множество точек P n-мерного пространства, определяемых n координатами (x1, x2,…,xn): P(x1, x2,…,xn)
|
| 21 | Скалярное поле | u = f(P) в области D – то же, что функция точки 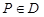
|
| 22 | Производная по направлению | пусть в плоской или пространственной области D задано скалярное поле u = f(P); в точке 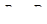 указано также вектором указано также вектором 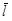 направление;
производная по направлению направление;
производная по направлению 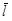 в P0 – это в P0 – это 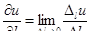 , где , где  – приращение u при смещении точки из P0 по направ-лению – приращение u при смещении точки из P0 по направ-лению 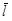 на величину Dl;
в плоском случае на величину Dl;
в плоском случае  и и 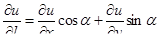 ;
в пространственном случае ;
в пространственном случае  и и 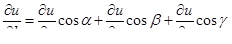
|
| 23 | Градиент скалярного поля (функции) u | вектор 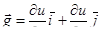 – в плоском случае, или – в плоском случае, или
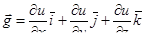 – в R3; – в R3;
 – орты осей координат – орты осей координат
|
| 24 | Дифференциал длины дуги | 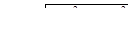 – плоская кривая, – плоская кривая,
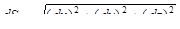 – пространственная кривая – пространственная кривая
|
| 1 | 2 | 3 |
| 25 | Векторная функция | 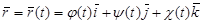 – векторное уравнение прост-ранственной линии (годографа этой векторной функции) – векторное уравнение прост-ранственной линии (годографа этой векторной функции)
|
| 26 | Нормальная плоскость | плоскость, проведенная через точку касания перпенди-кулярно касательной прямой |
| 27 | Натуральные уравнения кривой | параметрические уравнения, в которых параметр – длина дуги; векторная функция, у которой параметр – длина дуги: 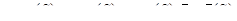
|
| 28 | Главная нормаль | прямая, идущая по вектору 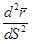 ; перпендикулярна каса-тельной (идущей по вектору ; перпендикулярна каса-тельной (идущей по вектору 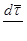 ) )
|
| 29 | Средняя кривизна кривой | абсолютная величина отношения угла Da поворота каса-тельной к длине дуги  , на которой произошел поворот , на которой произошел поворот
|
| 30 | Кривизна кривой в точке | предел средней кривизны, когда 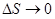 ;
кривизна ;
кривизна 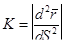 характеризует изогнутость кривой в точке
характеризует изогнутость кривой в точке
|
| 31 | Соприкасающаяся плоскость | плоскость, проведенная через касательную и главную нормаль; может быть получена как предельное положение плоскости, проходящей через три точки кривой: M1, M0, M2, когда 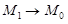 и и 
|
| 32 | Кручение кривой | предел отношения угла поворота бинормали, вызванного переходом из M0 в M, к длине дуги  при при 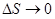 ;
мера отличия пространственной кривой от плоской (в точке M0) ;
мера отличия пространственной кривой от плоской (в точке M0)
|
| 33 | Бинормаль | прямая, идущая по вектору 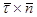 , где , где  – орт касательной, а – орт касательной, а  – орт главной нормали; перпендикулярна и касательной, и главной нормали – орт главной нормали; перпендикулярна и касательной, и главной нормали
|
| 34 | Интегральная сумма (Римана) функции f | сумма вида  , соответствующая заданной в замкнутой плоской области D функции f(x, y), произволь-ному разбиению D на площадки Di площадью DSi и выбору точек , соответствующая заданной в замкнутой плоской области D функции f(x, y), произволь-ному разбиению D на площадки Di площадью DSi и выбору точек 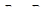
|
| 35 | Двойной интеграл | предел интегральных сумм при мелкости разбиений, стремящейся к нулю, и обозначается 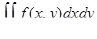
|
| 36 | Линейность двойного интеграла | свойство, состоящее в том, что
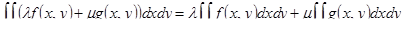 , для любых непрерывных в D функций f и g и постоянных l и m , для любых непрерывных в D функций f и g и постоянных l и m
|
| 37 | Аддитивность двойного интеграла по области интегрирования | свойство, состоящее в том, что для произвольного разбие-ния области D на области D1 и D2 без общих внутренних точек и непрерывной в D функции f имеет место равенство:

|
| 38 | Монотонность двойного интеграла | свойство, состоящее в том, что 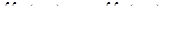 , для любых непрерывных в D функций f и g таких, что , для любых непрерывных в D функций f и g таких, что 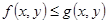 , , 
|
| 1 | 2 | 3 |
| 39 | Теорема о среднем для двойного интеграла | двойной интеграл от непрерывной в замкнутой области D функции f равен произведению площади S этой области на значение функции в некоторой точке P этой области:

|
| 40 | Тройной интеграл | предел интегральных сумм при условии, когда наибольший из диаметров всех подобластей Gi стремится к нулю, обозначаемый
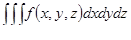
|
| 41 | Формула сведения двойного интеграла к повторному |  для правильной области для правильной области 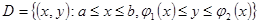 и непрерывной в D функции f и непрерывной в D функции f
|
| 42 | Формула сведения тройного интеграла к повторному |  для области
для области 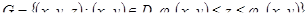
|
| 43 | Формула перехода к полярным координатам в двойном интеграле | 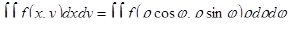 ,
где ,
где 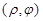 – полярные координаты точки – полярные координаты точки
|
| 44 | Формула перехода к цилиндрическим координатам в тройном интеграле | 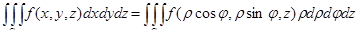 ,
где ,
где 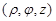 – цилиндрические координаты точки – цилиндрические координаты точки
|
| 45 | Интегральная сумма для криволинейного интеграла | сумма вида  , соответствующая заданной на кривой Г векторной функции , соответствующая заданной на кривой Г векторной функции 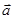 , выбранному на кривой непрерывному единичному касательному вектору , выбранному на кривой непрерывному единичному касательному вектору  , произвольному разбиению кривой Г на дуги Гi длины Dsi и выбору точек , произвольному разбиению кривой Г на дуги Гi длины Dsi и выбору точек 
|
| 46 | Криволинейный интеграл от вектор-функции 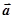 по кривой Г
по кривой Г
| предел интегральных сумм при условии 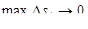 , обозначаемый , обозначаемый 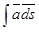 или или  , где P, Q, R – компоненты вектора , где P, Q, R – компоненты вектора 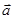
|
| 47 | Формула Грина | 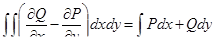 , где D – плоская область, ограниченная замкнутым кусочно-гладким контуром Г, а P и Q – функции, непрерывные в D вместе с частными производными , где D – плоская область, ограниченная замкнутым кусочно-гладким контуром Г, а P и Q – функции, непрерывные в D вместе с частными производными 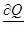 и и 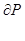 ; в криволинейном интеграле справа направление интегрирования соответствует обходу контура против часовой стрелки ; в криволинейном интеграле справа направление интегрирования соответствует обходу контура против часовой стрелки
|
| 48 | Поверхностный интеграл по верхней стороне поверхности s | предел интегральных сумм при условии, когда наибольший из диаметров площадок стремится к нулю, и обозначается 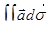 или или 
|
| 49 | Векторное поле | векторная функция, заданная в некоторой части прост-ранства или плоскости |
| 1 | 2 | 3 |
| 50 | Градиент 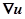 скалярного поля скалярного поля
| векторное поле, компонентами которого являются  , ,  , ,  , где u – скалярное поле , где u – скалярное поле
|
| 51 | Дивергенция 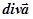 векторного поля векторного поля 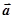
| скалярное поле  , где P, Q, R – компоненты исходного векторного поля , где P, Q, R – компоненты исходного векторного поля
|
| 52 | Ротор 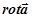 векторного поля векторного поля 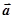
| векторное поле, компонентами которого являются  , где P, Q, R – компоненты исходного векторного поля , где P, Q, R – компоненты исходного векторного поля
|
| 53 | Циркуляция векторного поля по замкнутому контуру | криволинейный интеграл от соответствующей векторной функции по замкнутому контуру |
| 54 | Поток векторного поля через поверхность | поверхностный интеграл от соответствующей векторной функции по поверхности |
| 55 | Формула Стокса |  , где s – поверхность, стягиваемая замкнутым контуром Г, а компоненты P, Q, R векторного поля , где s – поверхность, стягиваемая замкнутым контуром Г, а компоненты P, Q, R векторного поля 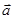 непрерывны и имеют непрерывные частные производные в некоторой области пространства, содержащей поверхность s непрерывны и имеют непрерывные частные производные в некоторой области пространства, содержащей поверхность s
|
| 56 | Формула Остроградского -Гаусса | 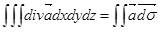 , где G – область в пространстве, ограниченная замкнутой поверхностью s, , где G – область в пространстве, ограниченная замкнутой поверхностью s, 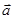 – непрерывное в G векторное поле с компонентами P, Q, R такое, что частные производные – непрерывное в G векторное поле с компонентами P, Q, R такое, что частные производные 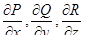 также непрерывны в G; в поверхностном интеграле справа поверхность s ориенти-рована внешней нормалью также непрерывны в G; в поверхностном интеграле справа поверхность s ориенти-рована внешней нормалью
|
| 57 | Соленоидальное векторное поле | непрерывное в области G векторное поле 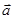 , если для любой ограниченной области , если для любой ограниченной области 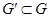 с кусочно-гладкой границей с кусочно-гладкой границей 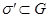 его поток через эту границу равен нулю его поток через эту границу равен нулю
|
| 58 | Потенциал векторного поля | такое скалярное поле, для которого данное векторное поле является градиентом |
| 59 | Потенциальное векторное поле | векторное поле, для которого существует потенциал |
Рабочий учебник в соответствии с балансовым методом проектирования образовательных программ содержит:
59 – приведенных понятий;
8 – дифференциальных компетенций.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ЮНИТА 6
Дифференциальное И ИНТЕГРАЛЬНОЕ исчисление
функциЙ нескольких переменных
Ответственный за выпуск Е.Д. Кожевникова
Корректор
Оператор компьютерной верстки А.А. Илюхин
___________________________________________________________________________________
НАЧОУ ВПО “Современная Гуманитарная Академия”
* Примечание. Знаком (*) отмечены учебные издания, на основе которых составлен тематический обзор.
* Полужирным шрифтом выделены новые понятия, которые необходимо усвоить. Знание этих понятий будет проверяться при тестировании.
Дата добавления: 2018-09-23; просмотров: 335; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
