Скорость и ускорение точки, движущейся по кривой

⇐ ПредыдущаяСтр 11 из 20Следующая ⇒

Пусть точка M движется по кривой L. Положение точки в момент t описывается координатами 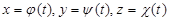или радиусом-вектором 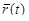. Таким образом, в уравнениях (11) или (2.12) кривой L параметр t теперь время. Пусть в момент t₀ положение точки M₀ характеризуется радиусом-вектором 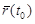. За время Dt от t₀ до t₀ + Dt точка переместится в позицию M, 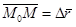(рис. 8) – вектор перемещения. Вектор 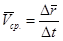– средняя скорость за время от t₀ до t₀ + Dt.

Мгновенная скорость в момент t₀ будет:

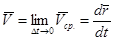(при t = t₀). (2.27)

Таким образом, скорость есть вектор, идущий по касательной прямой и направленный в сторону движения.

Модуль 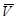, который мы обозначим V, есть согласно (2.16) и (2.17)

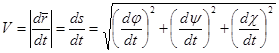. (2.28)

Из (2.27) следует

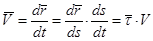, (2.29)

где 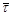– орт касательной. Для ускорения 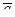в момент t = t₀ получаем:

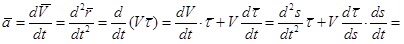
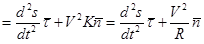(при t = t₀). (2.30)

Мы воспользовались формулами (2.23), (2.24), (2.28), (2.29). Таким образом, ускорение разложено на две компоненты: одна идет по касательной прямой и ее величина есть вторая производная от пути по времени, а другая – по главной нормали и ее величина есть квадрат модуля скорости, деленный на радиус кривизны.

О касательной плоскости к поверхности

Мы определили в разделе 1.2.3 касательную плоскость к поверхности как плоскость, натянутую на две прямые: одна из этих прямых была касательной к линии, получающейся на поверхности путем сечения плоскостью x = x₀, а другая – касательной к линии сечения плоскостью y = y₀. Однако, оказывается, справедлив гораздо более общий факт.

Теорема. Пусть p – касательная плоскость к поверхности

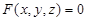(2.31)

в ее точке 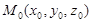. Касательная прямая в точке M₀ к любой линии на поверхности, проходящей через точку M₀, лежит в p.

Доказательство. Пусть линия L задана уравнениями (2.11). То, что линия L лежит на поверхности, означает, что все ее точки удовлетворяют уравнению (2.31):

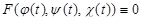. (2.32)

Равенство (2.32) является тождеством, оно справедливо при всех t.

Дифференцируя сложную функцию от t, получаем:

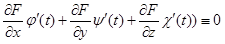. (2.33)

Пусть точке M₀ на поверхности отвечает значение параметра t = t₀ в уравнениях линии L, которая по условию проходит через эту точку:

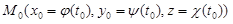Вектор 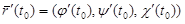идет по касательной прямой к линии L (см. подраздел 2.2.2), а вектор 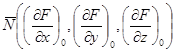(подраздел 1.3.7) направлен по нормали к поверхности. Условие (2.33) означает, что скалярное произведение 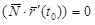. Значит, касательная прямая
к L перпендикулярна к нормали 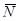и лежит в касательной плоскости.

Кратные и криволинейные интегралы

3.1. Определение кратного интеграла, условие существования
и свойства кратного интеграла

Ряд важных геометрических и физических задач приводит к интегрированию функций нескольких переменных. Конструкция кратного интеграла аналогична конструкции определенного интеграла для функции одной действительной переменной, заданной на отрезке числовой оси. Начнем со случая двух независимых переменных.

Рассмотрим заданную в ограниченной замкнутой области D плоскости xOy непрерывную функцию f(x, y). Разобьем произвольным образом область D на конечное число частей D_i площадью DS_i. Выберем точки 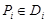(рис. 24). Мелкостью разбиения назовем наибольший из диаметров элементов разбиения (напомним, что под диаметром области понимается наибольшее расстояние между точками, лежащими на границе области).

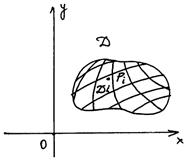
Рис. 24

Выражение 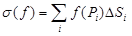(суммируем по всем элементам разбиения) называется интегральной суммой (Римана) функции f, соответствующей данному разбиению области D и фиксированному выбору точек .

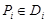Поведение интегральных сумм при уменьшении мелкости разбиений можно охарактеризовать следующим образом. Существует число I, удовлетворяющее условию: для любого положитель-ного (сколь угодно малого) числа e найдется такое положительное число d, что для всякого разбиения мелкости меньше чем d и при любом выборе точек P_i выполняется неравенство 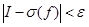. Это число I называется двойным интегралом от функции f по областиD и обозначается .

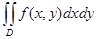Таким образом, можно сказать, что двойной интеграл есть предел интегральных сумм при мелкости разбиений, стремящейся к нулю. Если сделать разбиение достаточно мелким, то, независимо от выбора точек, принадлежащих элементам разбиения, интегральная сумма будет мало отличаться от двойного интеграла.

Отметим, что требование непрерывности функции в ограниченной замкнутой области является достаточным, но не необходимым условием для существования интеграла. Одним из необходимых условий существования интеграла является ограниченность функции. С другой стороны, интеграл существует и для многих ограниченных разрывных функций.

Из свойств интегральных сумм вытекают основные свойства двойного интеграла.

1. Если 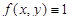в области D, то соответствующий интеграл 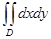равен площади S области D.

Действительно, в этом случае любая интегральная сумма s(f)равна S.

2. Для любых (непрерывных в D) функций f и g и постоянных l и m имеет место равенство:

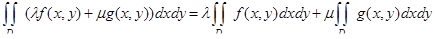Действительно, при любом разбиении области D на части D_i и выборе точек 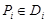, будем иметь:

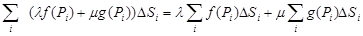, т.е. .

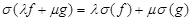Переходя в этом равенстве для интегральных сумм к пределу при мелкости разбиений, стремящейся к нулю, получим нужное равенство для интегралов. Свойство 2 называется линейностью двойного интеграла.

3. Для любого разбиения области D на подобласти D¢ и D¢¢и для любой (непрерывной в D) функции f имеет место равенство:

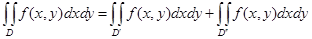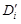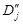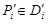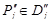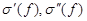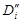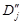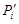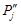Действительно, разобьем в свою очередь D¢ и D¢¢ на части , и выберем точки , . Соответствующие интегральные суммы обозначим . С другой стороны, рассмотрим такое разбиение области D, элементами которого являются все и с уже выбранными точками и . Мелкость этого общего разбиения равна большей из мелкостей разбиений подобластей D¢ и D¢¢. Интегральную сумму, соответствующую данному разбиению, обозначим s(f). Очевидно,

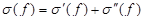Переходя в последнем равенстве к пределу, когда мелкости разбиений D¢ и D¢¢ стремятся к нулю (в этом случае мелкость соответствующего разбиения области D также стремится к нулю), получим свойство 3, которое называется аддитивностью двойного интеграла по области интегрирования.

4. Для любых (непрерывных в D) функций f и g таких, что 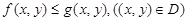имеет место неравенство

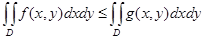Чтобы убедиться в этом, достаточно записать очевидное неравенство для интегральных сумм функций f и g:

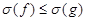
и перейти к пределу при мелкости разбиений, стремящейся к нулю.

Свойство 4 называется монотонностью двойного интеграла.

5. Для любой (непрерывной в D) функции f имеет место неравенство

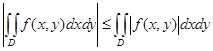Оно следует из свойства 4 и двойного неравенства

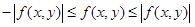
6. Для любой (непрерывной в D) функции f имеет место неравенство:

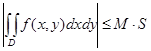где 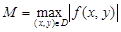, а S – площадь области D.

Свойство 6 следует из свойств 1, 2, 5 и неравенства

, .

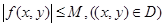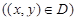Величина 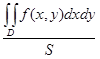называется средним значением функции f по области D. Имеет место следующая теорема о среднем.

Теорема 1. Если функция f непрерывна в ограниченной замкнутой области D, то внутри области D найдется точка P такая, что

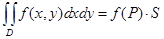Другими словами, непрерывная функция принимает среднее значение внутри области.

Для функции трех независимых переменных f(x, y, z), заданной в трехмерной области G, подобным образом вводится понятие тройного интеграла. Область G разбивается на части G_i объемом DV_i, выбираются точки 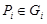и составляется интегральная сумма 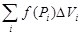. При условии непрерывности функции f в ограниченной замкнутой области G существует предел интегральных сумм, когда мелкость разбиений (т.е. наименьший из диаметров элементов разбиений) стремится к нулю. Этот предел называется тройным интегралом от функции f по области G и обозначается 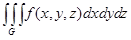. На тройной интеграл распространяются все основные свойства двойного интеграла (в 1 и 6 вместо площади S плоской области D в случае тройного интеграла следует писать объем V области G).

Дата добавления: 2018-09-23; просмотров: 382; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!