Определение поверхностного интеграла, его свойства
Рассмотрим гладкую поверхность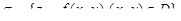 
, где функция f(x, y) непрерывна и имеет непрерывные частные производные в ограниченной замкнутой области D. Всякую непрерывную единичную нормаль на поверхности назовем ориентацией поверхности. Но в каждой точке поверхности s имеются лишь две единичные нормали: 
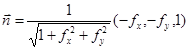и 
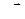, поэтому у поверхности s есть только две ориентации 
и 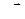. В том случае, когда выбирается нормаль , будем говорить о верхней стороне поверхности s, если же выбирается нормаль 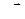– о нижней стороне.
Предположим, что на поверхности s задана вектор-функция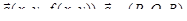 
, являющаяся непрерывной функцией переменных 
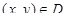. Умножив в каждой точке 
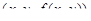поверхности вектор 
скалярно на , получим непрерывную на D числовую функцию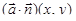 
.
Разобьем произвольным образом область D на части Di площадью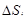 
и выберем точки 
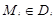. Площадь части поверхности s, которая проецируется на Di, приближенно равна
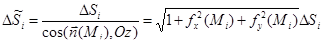
(степень приближения зависит от мелкости разбиения; написанное выражение есть в точности площадь куска проведенной в точке (Mi, f(Mi)) касательной плоскости, который проецируется на Di).
Умножим теперь значение функции 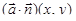в точке Mi на площадь 
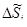и просуммируем по всем элементам разбиения. Используя координатную запись, будем иметь:
.
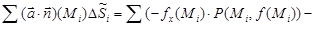
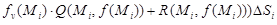Таким образом,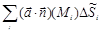 
есть интегральная сумма непрерывной на D функции 
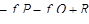. Следовательно, существует предел таких сумм при мелкости разбиений, стремящейся к нулю. Этот предел называется поверхностным интегралом от вектор-функции по верхней стороне поверхности s и обозначается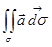 
или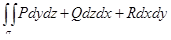 
. Используя вектор 
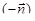вместо , получим определение поверхностного интеграла по нижней стороне поверхности s. Итак,
|
|
|
.
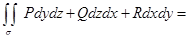
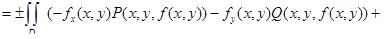
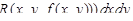Поверхностный интеграл, конечно, обладает свойствами линейности, аддитивности и, кроме того, меняет знак при изменении ориентации поверхности.
Мы рассмотрели случай, когда поверхность однозначно проецируется на область D координатной плоскости Oxy. В случае, если поверхность однозначно проецируется на область D, например координатной плоскости Oxz, и является графиком непрерывно дифференцируемой функции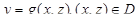 
, формула для вычисления поверхностного интеграла примет следующий вид:
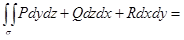
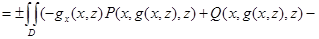
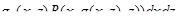
(знак “+” выбирается в случае, когда нормаль составляет острый угол с положительным направлением оси Oy; в противном случае берется знак “–”).
Произвольную гладкую поверхность s всегда можно разбить на конечное число частей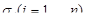 
, допускающих явное задание. По определению получаем:
.
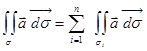Ориентация каждой части должна, конечно, соответствовать исходной ориентации на s.
Аналогично поступают и в случае кусочно-гладкой поверхности s – результата “склейки вдоль краев” конечного числа гладких поверхностей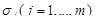 
. Интеграл по такой поверхности определяется как сумма интегралов по гладким частям (при этом все 
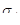должны быть согласованно ориентированы).
|
|
|
Пример. Вычислить интеграл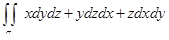 
по верхней стороне параболоида 
.
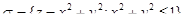Решение. Имеем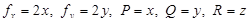 
, и
.
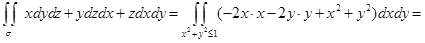
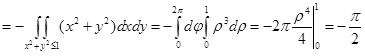Формула Стокса
Всюду далее числовые функции, заданные в некоторой части пространства, будем называть скалярными полями, а векторные функции – векторными полями. Заданное в области G поле (скалярное или векторное) называется непрерывно дифференцируемым, если все его частные производные первого порядка непрерывны на G. Всякому непрерывно дифференцируемому на G скалярному полю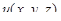 
соответствует непрерывное на G векторное поле его градиентов
.
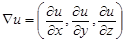Всякому же непрерывно дифференцируемому на G векторному полю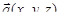 
можно поставить в соответствие следующие непрерывные на G скалярное поле 
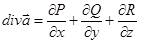и векторное поле
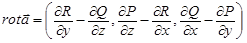
(P, Q, R есть координаты вектора ).
Скалярное поле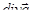 
называется дивергенцией векторного поля , а векторное поле 
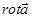называется вихрем (ротором) векторного поля .
Если Г – кусочно-гладкий замкнутый контур и векторное поле задано на Г, то криволинейный интеграл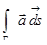 
называется циркуляцией векторного поля по этому контуру. Если s – кусочно-гладкая поверхность, то для векторного поля , заданного на поверхности s, поверхностный интеграл 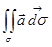называется также потоком векторного поля через поверхность s.
|
|
|
Пусть D – замкнутая плоская область, границей которой служит кусочно-гладкий контур Г0. Рассмотрим гладкую поверхность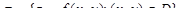 
. Обозначим Г образ контура Г0 при отображении f. Контур Г есть край поверхности s, тогда Г0 – его проекция на плоскость Oxy. На контуре Г0 выберем ориентацию, при которой он проходится против часовой стрелки. Ориентация Г0 порождает ориентацию на Г. На поверхности s выберем ориентацию, при которой нормаль во всех точках поверхности образует острый угол с осью Oz:
.
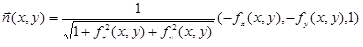Такие ориентации на поверхности s и ее крае Г называются согласованными (рис. 35).
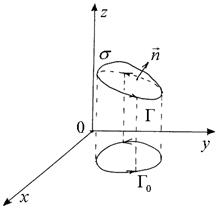
Рис. 35
Теорема 4.Если векторное поле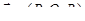 
непрерывно дифференцируемо в некоторой области пространства, содержащей поверхность s, то имеет место равенство
,
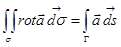называемое формулой Стокса.
Эта формула означает, что поток вихря векторного поля через поверхность равен циркуляции векторного поля по краю поверхности, ориентированному согласованно с нормалью к поверхности.
В координатной записи формула Стокса имеет вид:
|
|
|
.
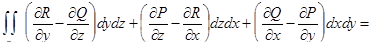
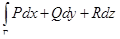При вычислениях формулу Стокса обычно используют справа налево: по заданному векторному полю легко найти вихрь, но не наоборот. Кроме того, при использовании формулы Стокса для нахождения циркуляции вдоль заданного контура Г, в качестве s можно брать любую гладкую поверхность, стягивающую Г, на которой поле непрерывно дифференцируемо. Например, если контур Г плоский, то в качестве s можно взять плоскую поверхность, ограниченную этим контуром.
Пример. Вычислить интеграл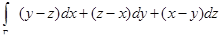 
, где Г – эллипс в сечении цилиндра 
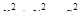плоскостью 
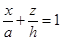(пробегаемый против хода часовой стрелки, если смотреть из точки (2a, 0, 0)) (рис. 36).
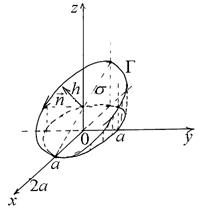
Рис. 36
Решение. Имеем:
.
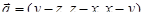Тогда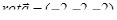 
. В качестве поверхности s, натянутой на контур Г, берем 
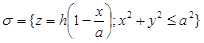. По формуле Стокса исходный интеграл равен интегралу
.
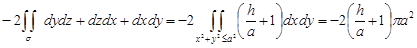Дата добавления: 2018-09-23; просмотров: 227; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!