Формула Остроградского–Гаусса
Теорема 5. Пусть G – замкнутая область в пространстве, ограниченная замкнутой кусочно-гладкой поверхностью s, а векторное поле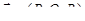 
непрерывно дифференцируемо на G. Тогда имеет место равенство
,
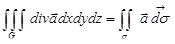где интеграл в правой части берется по внешней стороне (нормаль направлена во внешность области) поверхности s, ограничивающей область G. Это равенство называется формулой Остроградского–Гаусса и означает, что интеграл по области от дивергенции векторного поля равен потоку этого поля через поверхность, ограничивающую область, в направлении внешней нормали. В координатной форме формула Остроградского–Гаусса выглядит следующим образом:
.
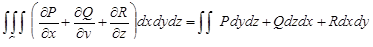Формулу Остроградского–Гаусса чаще используют при вычислении поверхностных интегралов, сводя их к тройным.
Пример. Вычислить интеграл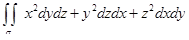 
, где s – внешняя сторона границы куба 
.
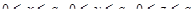Решение. Имеем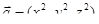 
. Тогда 
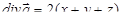. В силу формулы Остроградского–Гаусса исходный интеграл равен интегралу
.
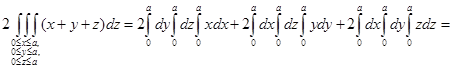
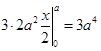Формулу Остроградского–Гаусса можно использовать и слева направо. Так, положив в ней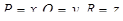 
, получим выражение для объема области в виде поверхностного интеграла:
.
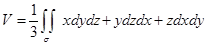Соленоидальные и потенциальные векторные поля
Важными классами векторных полей являются соленоидальные поля и потенциальные поля. Можно показать, что при достаточно общих предположениях любое векторное поле раскла-дывается в сумму потенциального и соленоидального векторных полей.
|
|
|
Непрерывное в области G векторное поле 
называется соленоидальным в этой области, если для любой ограниченной области 
с кусочно-гладкой границей 
его поток через эту границу равен нулю.
Теорема 6. Для того чтобы непрерывно дифференцируемое в некоторой области векторное поле было соленоидальным, необходимо и достаточно, чтобы во всех точках этой области его дивергенция равнялась нулю: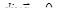 
.
Примером соленоидального в некоторой области G поля является поле вихря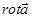 
, заданного на G, дважды непрерывно дифференцируемого векторного поля (последнее означает, что вектор-функция имеет в G непрерывные частные производные второго порядка). В силу теоремы 6 достаточно проверить, что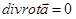 
в G. Действительно, если 
, то 
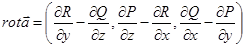, и
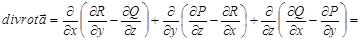
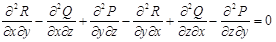
(из непрерывности смешанных производных следует, что они не зависят от порядка дифференци-рования).
Если в области G задано векторное поле и существует скалярное в G поле u, для которого векторное поле является полем градиентов: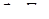 
, то функция u называется потенциалом векторного поля 
. Векторное поле, для которого существует потенциал, называется потенциальным полем. Таким образом, в случае потенциального векторного поля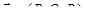 
, его компоненты являются производными некоторой функции u:
|
|
|
,
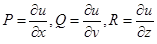а дифференциальная форма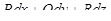 
является полным дифференциалом:
.
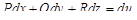Очевидно, потенциал определен неоднозначно, с точностью до постоянного слагаемого.
Предположим теперь, что заданное в области G потенциальное векторное поле 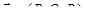непрерывно в G, u – его потенциал, и 
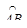– гладкая кривая, лежащая в области G, началом которой является точка A, а концом – точка B:
.
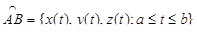Рассмотрим криволинейный интеграл
.
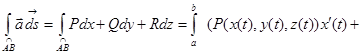
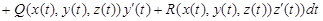Подставляя 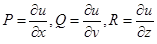и применяя формулу дифференцирования сложной функции, будем иметь:
.
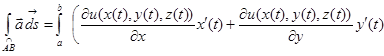
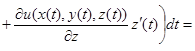
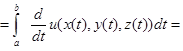
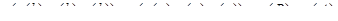Таким образом, для потенциального поля криволинейный интеграл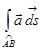 
не зависит от выбора гладкой кривой, соединяющей в области G точки A и B, и равен разности потенциалов в конечной и начальной точках. Это утверждение очевидным образом распространяется и на кусочно-гладкие кривые. В частности, для лежащего в G замкнутого кусочно-гладкого контура Г криволинейный интеграл 
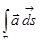равен нулю (точки A и B совпадают). Несложно показать и обратное: из равенства нулю циркуляции по любому замкнутому контуру следует, что поле потенциально.
Таким образом, имеет место следующий критерий потенциальности векторного поля:
Теорема 7. Для того чтобы непрерывное векторное поле было потенциальным в области, необходимо и достаточно, чтобы его циркуляция по любому кусочно-гладкому замкнутому контуру, лежащему в этой области, равнялась нулю.
|
|
|
Необходимое и достаточное условие в теореме, однако, трудно проверяемо. Для широкого класса областей существует более удобный критерий потенциальности.
Область называется односвязной, если любой лежащий в G кусочно-гладкий замкнутый контур можно непрерывной деформацией в G стянуть в точку. Примером односвязной области является всякая выпуклая область, примером неодносвязной области служит тор.
Теорема 8. Для того чтобы непрерывно дифференцируемое векторное поле было потенциальным в односвязной области, необходимо и достаточно, чтобы его вихрь в этой области равнялся нулю.
Заметим, что условие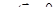 
в G является необходимым в случае произвольной области G, без предположения односвязности. Действительно,
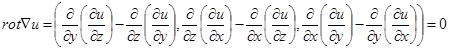. Таким образом, потенциальные поля являются безвихревыми. В случае же односвязной области верно и обратное: безвихревое поле будет потенциальным.
Формула
,
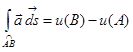справедливая для потенциального поля , оказывается полезной как для вычисления криволи-нейных интегралов, если известен потенциал, так и для нахождения потенциала. Зафиксировав любую точку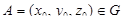 
, можно считать потенциал в этой точке равным нулю: 
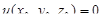. Тогда для точки 
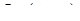будем иметь:
|
|
|
,
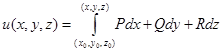причем, согласно сделанному замечанию, путь интегрирования можно выбирать произвольным.
Пример. Проверить, является ли поле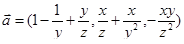 
потенциальным в четверть-пространстве x > 0, z > 0, и найти его потенциал.
Решение. Согласно теореме 8, достаточно проверить условие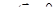 
. Имеем:
, 
; 
; 
.
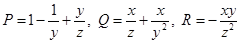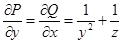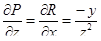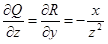Таким образом, поле потенциально. Для нахождения потенциала рассмотрим интеграл
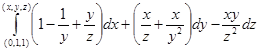
вдоль ломаной 
, соединяющей точки A(0,1,1) и B(x, y, z) (рис. 37; звенья ломаной параллельны координатным осям). Очевидно,
.
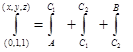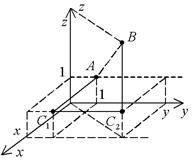
Рис. 37
При этом
,
,
.
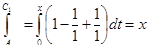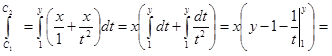
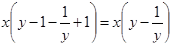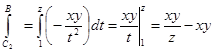Итак,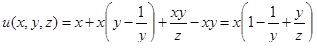 
.
3.11. Геометрические и физические приложения кратных,
криволинейных и поверхностных интегралов
С применением кратных интегралов при нахождении площадей и объемов мы уже сталки-вались ранее (см. юниту 3). Перечислим следующие механические и физические приложения кратных интегралов.
1) Если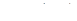 
– плотность плоской пластинки D, то ее масса
,
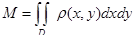а координаты ее центра тяжести
.
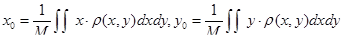2) Моменты инерции пластинки D, лежащей в плоскости xy, относительно координатных осей x и y выражаются соответственно формулами:
.
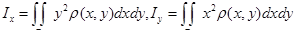3) Если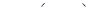 
– плотность тела G в точке (x, y, z), то масса тела равна
,
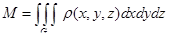а координаты центра тяжести вычисляются по формулам:
.
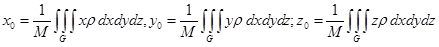4) Моменты инерции тела G относительно координатных плоскостей xy, yz, zx выражаются соответственно формулами:
.
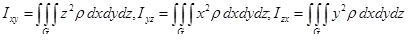5) Момент инерции тела G относительно некоторой оси l вычисляется по формуле
,
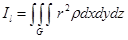где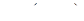 
– расстояние от точки 
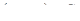до оси l.
В частности, для координатных осей имеем:
.
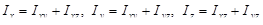6) Момент инерции тела G относительно начала координат вычисляется по формуле:
.
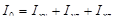7) Потенциал поля тяготения, создаваемого телом G с плотностью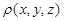 
, в точке 
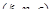равен
,
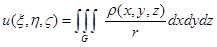где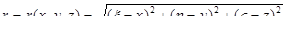 
– расстояние от переменной точки 
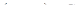до фиксированной точки .
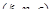8) Если плотность распределения заряда в области G равна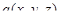 
, то заряд, сосредоточенный в G, равен
,
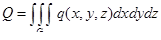а кулоновский потенциал, создаваемый этим зарядом в точке 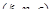, равен
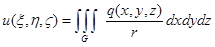, где r – расстояние от точки (x, y, z) до точки .
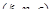Перечислим теперь некоторые физические приложения криволинейных и поверхностных интегралов.
9) Работа переменной силы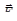 
, точка приложения которой описывает кривую Г, равна
.
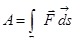Если силовое поле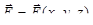 
потенциально и 
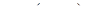– его потенциал, то работа, совершаемая полем при перемещении из точки P1 в точку P2, равна
.
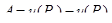10) Если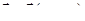 
есть поле скоростей жидкости, то количество жидкости, протекающее через поверхность s, выражается формулой:
.
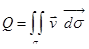Соленоидальность поля скоростей в области означает отсутствие в этой области источников жидкости (расход жидкости через любую замкнутую поверхность, лежащую в области, равен нулю).
Дата добавления: 2018-09-23; просмотров: 680; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!