Пример выполнения упражнения тренинга на компетенцию 1
Задание
Вычислите производные первых и вторых порядков функции  .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Вычислить первые производные:
а) считая y постоянным, дифференцируем функцию z = f(x, y) по переменному x – находим частную производную 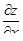 по x;
б) частную производную по y – по x;
б) частную производную по y – 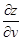 находим аналогично, фиксируя x находим аналогично, фиксируя x
|
а)  ;
б) ;
б) 
|
| 2 | Вычислить вторые производные  и и  :
а) считая y постоянным, дифференцируем :
а) считая y постоянным, дифференцируем 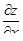 по переменному x – получаем по переменному x – получаем  ;
б) считая x постоянным, дифференцируем ;
б) считая x постоянным, дифференцируем 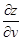 по переменному y – получаем по переменному y – получаем 
|
а) 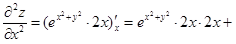
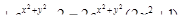 ;
б) ;
б) 
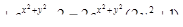
|
| 3 | Вычислить смешанные производные:
а) считая x постоянным, дифференцируем 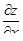 по переменному y – находим по переменному y – находим  ;
б) считая y постоянным, дифференцируем ;
б) считая y постоянным, дифференцируем 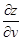 по переменному x – находим по переменному x – находим 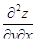 ;
в) сравнивая полученные производные, убеждаемся, что ;
в) сравнивая полученные производные, убеждаемся, что
 = = 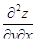
| а) 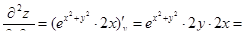
 ;
б) ;
б) 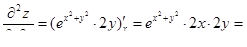
 ;
в) найденные производные равны ;
в) найденные производные равны
|
Вычислите самостоятельно частные производные первого и второго порядков следующих функций:
1.1.  .
.
1.2.  .
.
1.3.  .
.
1.4. 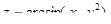 .
.
1.5. 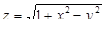 .
.
1.6.  .
.
Пример выполнения упражнения тренинга на компетенцию 2
Задание
Запишите уравнение касательной плоскости и найдите полный дифференциал функции 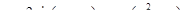 в точке
в точке  .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Вычислить частные производные  , , 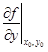 и и 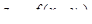
|  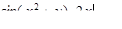 = 2(–1) = – 2;
= 2(–1) = – 2;
 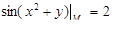 ;
z0 = –1 ;
z0 = –1
|
| 2 | Подставить полученные значения в уравнение касательной плоскости
 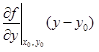
| 
|
| 3 | Найти полный дифференциал

| 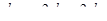
|
Вычислите самостоятельно полный дифференциал следующих функций:
2.1. 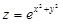 в точке
в точке  .
.
2.2.  в точке
в точке 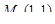
2.3. 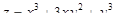 в точке
в точке 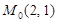
Найдите уравнение касательной плоскости следующих функций:
2.4. 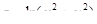 в точке
в точке 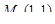
2.5. 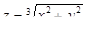 в точке
в точке 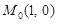
Пример выполнения упражнения тренинга на компетенцию 3
Задание
Исследуйте на экстремум функцию  .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Найти область определения | 
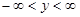
|
| 2 | Найти частные производные 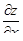 и и 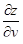
| 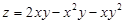 ; ;
 ; ;
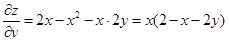
|
| 3 | Найти точки, в которых 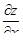 и и 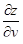 равны нулю или не существуют, т.е. критические точки (необходимое условие наличия экстремума) равны нулю или не существуют, т.е. критические точки (необходимое условие наличия экстремума)
| Частные производные всюду существуют.
Найдем точки, где они равны нулю:
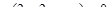
 Решив систему, получим координаты точек:
Решив систему, получим координаты точек:
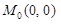 , , 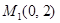 , , 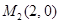 , , 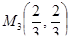
|
| 4 | Найти
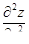 , ,  , , 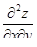
| 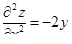 ; ; 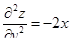 ; ; 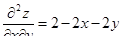
|
| 5 | Вычислить значения частных про-изводных второго порядка в крити-ческих точках | 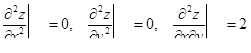 ; ;
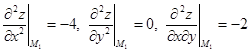 ; ;
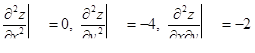 ; ;
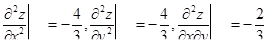
|
| 6 | Использовать достаточное условие наличия экстремума. Составить
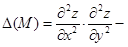 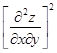 и вычислить его значения в крити-ческих точках
и вычислить его значения в крити-ческих точках
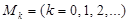
| 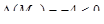 ; ;
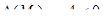 ; ;
 ; ;

|
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 7 | Сделать вывод о наличии экстре-мума:
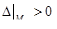 – экстремум есть; – экстремум есть;
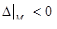 – экстремума нет; – экстремума нет;
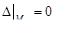 – неопределенный случай – неопределенный случай
| В точках M0 , M1, M2 – экстремума нет; в точке M3 – экстремум есть |
| 8 | По знаку второй производной в точке M установить характер экстремума:
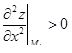 – точка минимума; – точка минимума;
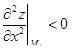 – точка максимума – точка максимума
| 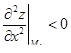 M3 – точка максимума
M3 – точка максимума
|
| 9 | Вычислить экстремальное значение функции | 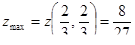
|
Исследуйте самостоятельно на экстремум следующие функции:
3.1.  .
.
3.2.  .
.
3.3. 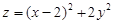 .
.
3.4.  .
.
3.5.  .
.
Дата добавления: 2018-09-23; просмотров: 178; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
