Пример выполнения упражнения тренинга на компетенцию 4
Задание
Найти наибольшее и наименьшее значения функции 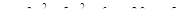 в замкнутом треугольнике, ограниченном осями координат и прямой x + y = 5.
в замкнутом треугольнике, ограниченном осями координат и прямой x + y = 5.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Сделать чертеж области D | 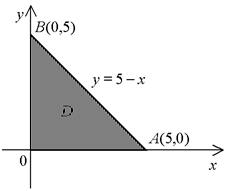
|
| 2 | Найти стационарные точки, лежа-щие внутри D | 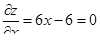 ; ; 
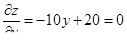 ; ; 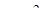 Стационарная точка
Стационарная точка 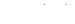 лежит внутри области. лежит внутри области.
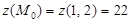
|
| 3 | Исследовать функцию на границе области. Подставить в функцию уравнение границы и найти наи-меньшее и наибольшее значения полученной функции одной пере-менной – параметра, к которому отнесены линии, ограничивающие область D | 1. На оси Ox:
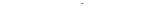 , , 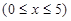 ; ;
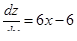 ;
6x – 6 = 0, x = 1;
z(1,0) = 2;
на границах отрезка: ;
6x – 6 = 0, x = 1;
z(1,0) = 2;
на границах отрезка:
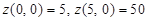 . .
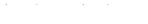 . .
 .
2. На оси Oy:
x = 0, .
2. На оси Oy:
x = 0, 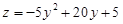
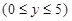
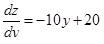 ; ;  , y = 2
Вычисляем значения функции в стационарной точке y = 2 и на границах отрезка при y = 0 и y = 5: , y = 2
Вычисляем значения функции в стационарной точке y = 2 и на границах отрезка при y = 0 и y = 5:
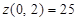 , , 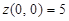 , , 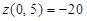 . .
 ; ;
|
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
3. На отрезке прямой AB:
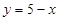 , ,
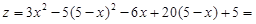
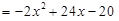 ; ;
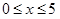 ; ;
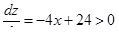 на рассматриваемом интервале, т.е. функция монотонна, а концы интервала x = 0 и x = 5 дают уже встречающиеся точки A(5, 0) и B(0, 5) на рассматриваемом интервале, т.е. функция монотонна, а концы интервала x = 0 и x = 5 дают уже встречающиеся точки A(5, 0) и B(0, 5)
| ||
| 4 | Сравнить все вычисленные значе-ния функции в отдельных точках и найти среди них наименьшее и наибольшее, которые и будут соот-ветственно наименьшим и наиболь-шим значением функции в области D | Имеем:
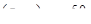 , ,
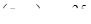 , ,
 , ,
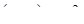 , ,
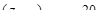 .
Получаем:
наименьшее значение .
Получаем:
наименьшее значение
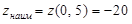 ;
наибольшее значение ;
наибольшее значение
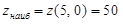
|
Найдите самостоятельно наибольшее и наименьшее значения функций:
|
|
|
4.1. 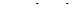 в круге
в круге  .
.
4.2. 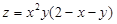 в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми 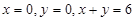 .
.
4.3.  в прямоугольнике, ограниченном прямыми
в прямоугольнике, ограниченном прямыми 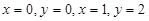 .
.
Пример выполнения упражнения тренинга на компетенцию 5
Задание
Для функции 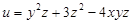 в точке
в точке 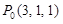 найдите градиент и производную в направлении
найдите градиент и производную в направлении  .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Вычислить частные производные функции u = f(x, y, z) по переменным x, y, z в точке 
| 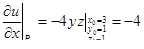 , ,
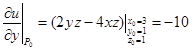 , ,
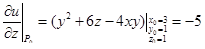
|
| 2 | Вычислить градиент функции u = f(x, y, z) в точке  по формуле: по формуле:
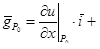 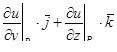
| 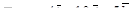
|
| 3 | Вычислить производную по направ-лению 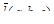 в точке в точке  : :
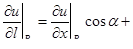 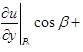
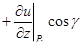 ;
направляющие косинусы ;
направляющие косинусы 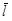 находятся по формуле: находятся по формуле: 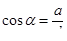 , , 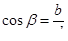 , , 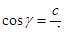 ,
где ,
где  , ,
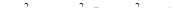 .
Примечание: В случае двух перемен-ных применяем аналогичные формулы: .
Примечание: В случае двух перемен-ных применяем аналогичные формулы:
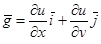 , ,
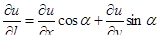 ,
где теперь ,
где теперь 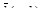 , , 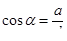 , , 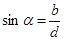 , , 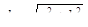
| 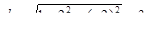 , ,
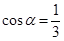 , , 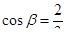 , , 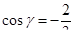 , ,
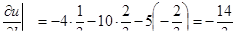
|
Найдите градиент скалярного поля:
5.1. 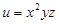 в точке (1, 2, –3).
в точке (1, 2, –3).
5.2.  в точке (0, 0).
в точке (0, 0).
5.3. 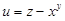 в точке (1, –1, 2).
в точке (1, –1, 2).
Найдите производную:
5.4. Скалярного поля 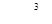 в точке (1, –2) в направлении вектора
в точке (1, –2) в направлении вектора 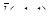 .
.
5.5. Функции 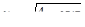 в точке (–1, 1, –1) в направлении вектора
в точке (–1, 1, –1) в направлении вектора 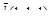 .
.
5.6. Функции 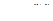 в точке (2, –2) в направлении ее градиента в этой точке.
в точке (2, –2) в направлении ее градиента в этой точке.
Найдите наибольшую скорость возрастания функции:
|
|
|
5.7. 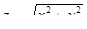 при переходе через точку
при переходе через точку 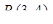 .
.
Пример выполнения упражнения тренинга на компетенцию 6
Задание
Напишите уравнение касательной плоскости и уравнение нормали к сфере 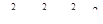 в точке
в точке 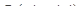 .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данного задания предложенному алгоритму |
| 1 | Вычислить 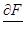 , , 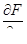 , , 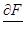 и подста-вить в них координаты и подста-вить в них координаты  заданной точки заданной точки
| Подстановкой координат P0 в уравнение поверхности убеждаемся, что P0 лежит на сфере
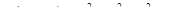 . .
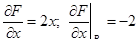 ; ;
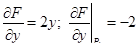 ; ;
|
| 2 | Записать уравнение касательной плоскости:
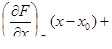 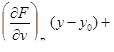
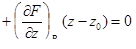
| (–2)(x + 1) – 2(y + 1) + 2(z – 1) = 0, x – y + z – 6 = 0 |
| 3 | Записать уравнение нормали:
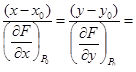 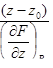
| 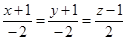
|
Решите самостоятельно.
Дано уравнение поверхности F(x, y, z) = 0 и точка P0 на ней.
6.1. Напишите уравнение касательной плоскости к поверхности в точке P0.
а) 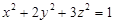 (эллипсоид),
(эллипсоид), 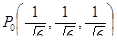 .
.
б)  (эллиптический параболоид) в точке (1, 1, ?).
(эллиптический параболоид) в точке (1, 1, ?).
6.2. Напишите уравнения нормали к конусу 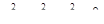 в точке
в точке 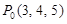 .
.
Дата добавления: 2018-09-23; просмотров: 217; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
