Замена переменных в кратном интеграле
Формулу замены переменных в двойном интеграле рассмотрим на примере вычисления двойного интеграла в полярных координатах.
Пусть на плоскости задана декартова система координат Oxy. Введем на плоскости полярную систему координат, взяв за полюс начало координат, а за полярную ось – ось x. Полярными координатами точки называется пара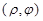 
, где 
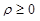– расстояние от точки до полюса, а 
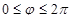– угол, который образует с полярной осью радиус-вектор точки. Полярные координаты однозначно определяют положение точки на плоскости. Связь между декартовыми и полярными координатами представляется формулами 
, 
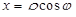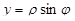(рис. 31).
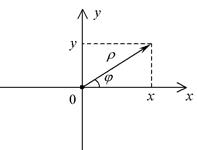
Рис. 31
Пусть D – ограниченная замкнутая область на плоскости xOy, уравнение границы которой имеет вид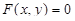 
, а сама область D состоит из точек, для которых 
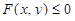. При вычислении двойного интеграла от непрерывной функции f(x, y) по области D можно пользоваться формулой перехода к полярным координатам:
.
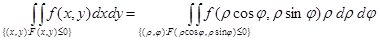При использовании данной формулы надо вместо аргументов x и y исходной функции подставить выражения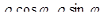 
, полученную функцию переменных r и j умножить на r и проинтегрировать по области D, перейдя в неравенстве для области к полярным координатам.
Поясним появление множителя r в подынтегральном выражении. Используя независимость двойного интеграла от способа разбиения, будем разбивать область интегрирования на части Di координатной сеткой полярной системы координат, т.е. концентрическими окружностями с центром в начале координат и лучами, исходящими из начала координат. Рассмотрим те элементы разбиения Di, которые не пересекаются с границей области. При достаточно мелком разбиении их можно считать прямоугольниками со сторонам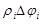и 
и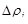 
(рис. 32). С другой стороны, слагаемые в интегральной сумме, отвечающие тем Di, которые пересекаются с границей области, при измельчении разбиений не окажут влияния на величину предела. Поэтому интегральную сумму 
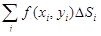можно заменить на 
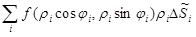, где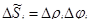 
.
|
|
|
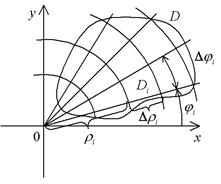
Рис. 32
Последняя есть интегральная сумма функции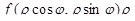 
, определенной на соответствующей области D части 
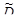плоскости переменных r, j, где роль декартовой системы координат играют полярные координаты. При мелкости разбиений, стремящейся к нулю, она имеет своим пределом двойной интеграл 
.
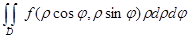Переход к полярным координатам часто приводит к упрощению подынтегрального выражения и (или) области интегрирования.
Пример 1. Вычислить интеграл от функции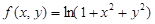 
по кругу 
.
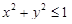Решение. Используя формулу перехода к полярным координатам, будем иметь:
.
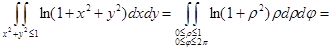
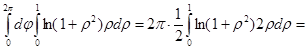
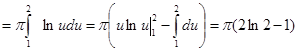При вычислении тройных интегралов часто пользуются цилиндрическими или сферическими координатами.
Зафиксировав в пространстве декартову систему координат Oxyz, цилиндрическими координатами точки назовем тройку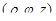 
, где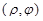 
– полярные координаты проекции точки на плоскость Oxy (рис. 33). Сферическими координатами точки называется тройка 
,
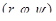где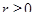 
– расстояние от точки до начала координат, 
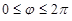– то же, что и в случае цилиндрических координат, 
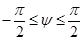– угол, образованный радиус-вектором точки и плоскостью (рис. 34).
|
|
|
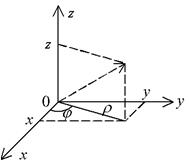
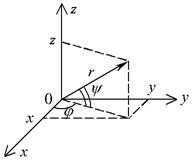
Рис. 33 Рис. 34
Связь между сферическими и декартовыми координатами выражается формулами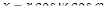 
, 
.
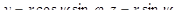При вычислении тройного интеграла в цилиндрических координатах пользуются формулой:
,
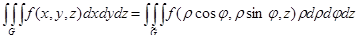а в сферических координатах – формулой:
,
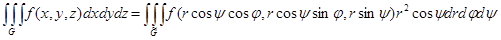где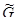 
– соответствующая области G часть пространства переменных 
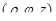или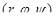 
.
Аналогично двойному интегралу возникновение множителей r и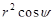 
при переходе к цилиндрическим и сферическим координатам становится понятным, если использовать специальное разбиение области на части координатной сеткой соответствующей системы координат. Так, при малых 
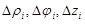объем параллелепипеда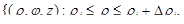 
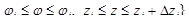цилиндрической системы координат есть 
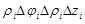, а при малых 
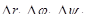объем параллелепипеда
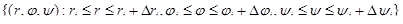
сферической системы координат есть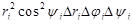 
.
|
|
|
Приведем пример вычисления тройного интеграла в сферических координатах.
Пример 2. Вычислить интеграл от функции
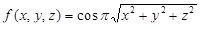по шару 
.
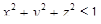Решение. Имеем:
.
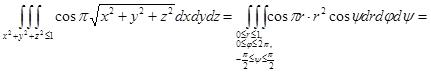
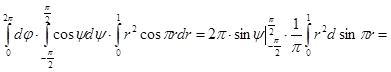
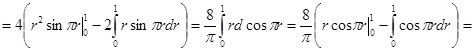
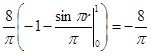Площадь поверхности
Рассмотрим гладкую поверхность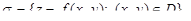 
где функция f(x, y) непрерывна и имеет непрерывные частные производные в ограниченной замкнутой области D. Как известно, уравнение касательной плоскости в точке 
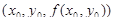поверхности имеет вид:
.
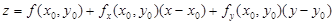Соответственно, нормаль к поверхности задается уравнением:
.
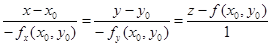Возьмем в каждой точке поверхности единичный вектор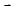 
нормали, образующий острый угол с осью Oz:
.
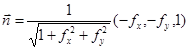Очевидно,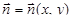 
есть непрерывная вектор-функция на D.
Разобьем произвольным образом область D на части Di площадью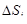 
и выберем точки 
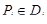. В каждой точке 
поверхности s проведем касательную плоскость и рассмотрим часть s i поверхности и часть p i касательной плоскости, проецирующиеся в область Di.
При достаточно мелком разбиении области D площадь части s i можно приближенно заменить площадью части , которая равна
.
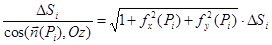За площадь поверхности s принимают предел суммы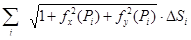 
этих площадей по всем элементам разбиения, когда мелкость разбиения стремится к нулю. Этот предел существует, поскольку написанная сумма является интегральной суммой непрерывной в D функции 
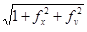, и равен двойному интегралу 
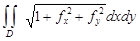. Таким образом, площадь гладкой поверхности 
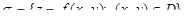вычисляется по формуле:
|
|
|
.
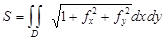Пример. Вычислить площадь поверхности
.
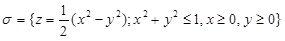Решение. Имеем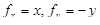 
, и
.
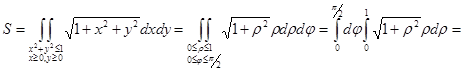
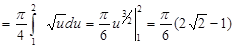Дата добавления: 2018-09-23; просмотров: 456; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!