Касательная к пространственной кривой
Рассмотрим линию L, задаваемую векторной функцией (2.12). Как обычно, касательная прямая определяется как предельное положение секущей. Возьмем точку 
, которая соответствует начальному значению t0 параметра. Дадим t приращение Dt. Значению t0 + Dt отвечает значение радиуса-вектора, определяющее точку M на линии L.
Тогда (рис. 21):
;
;
.
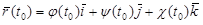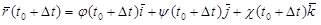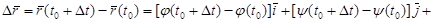
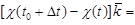
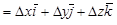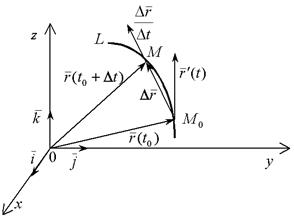
Рис. 21
Функции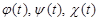 
здесь и далее считаем дифференцируемыми и поэтому все дальнейшие выкладки законны:
.
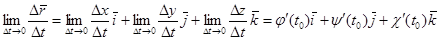Получившееся выражение и следует понимать как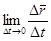 
и считать производной 
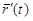от векторной функции 
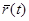, вычисленной при t = t0:
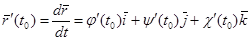. (2.13)
При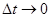 
точка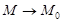 
и вектор 
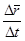, идущий по секущей M0M, стремится к предельному положению 
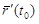, которое тем самым идет по касательной к линии. Итак, производная 
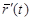служит направляющим вектором касательной прямой. Поэтому уравнения касательной можно записать в виде:
, 
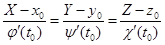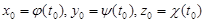. (2.14)
Здесь (X, Y, Z) – координаты текущей точки касательной, а x0, y0, z0 – координаты точки касания.
Более внимательное рассмотрение вектора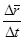 
показывает, что он направлен в сторону движения по кривой, соответствующего возрастанию параметра t (Dt > 0). Поэтому и предельное положение 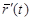этого вектора направлено в сторону, соответствующую движению по L, отвечающему возрастанию t.
Нормальная плоскость
Плоскость, проведенная через точку касания M0 перпендикулярно касательной прямой называется нормальной плоскостью к кривой в этой точке. Ее уравнение имеет вид:
|
|
|
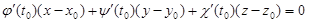, (2.15)
где t0 – значение параметра, отвечающее точке ; x0, y0, z0 – координаты M0; x, y, z – координаты текущей точки плоскости.
Дифференциал длины дуги
Из формулы (2.13) получаем, что (t – произвольное значение параметра):
;
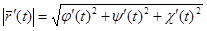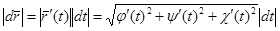. (2.16)
Будем от некоторой начальной точки A на кривой L отсчитывать длину дуги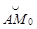 
до произвольной точки (рис. 22).
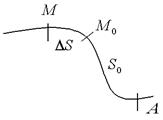
Рис. 22
Вернувшись к рис. 21, видим, что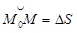 
стягивается вектором 
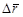. При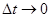 
считаем, как обычно, что две б.м. DS и 
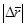эквивалентны. Тогда:
,
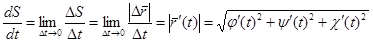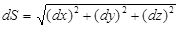(2.17)
( 
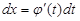и т.д.).
Формула (2.17) – обобщение формулы (2.3) для плоских кривых из раздела 1.1.
Натуральные уравнения кривой. Главная нормаль
Наиболее удобным по ряду причин является случай, когда в параметрических уравнениях (2.11) в качестве параметра взята длина дуги S на этой кривой:
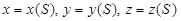. (2.18)
Такие уравнения называют натуральными уравнениями кривой. В этом случае, как следует из сравнения (2.17) и (2.16)
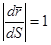, (2.19)
|
|
|
т.е. производная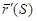 
является вектором единичной длины, направленным по касательной (ортом касательной) в сторону движения, отвечающего возрастанию S.
Обозначим этот вектор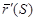 
через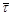 
и найдем 
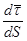, т.е. 
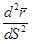. Исходим из того, что скалярное произведение 
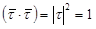. Дифференцируется скалярное произведение двух векторных функций по тем же правилам, что и произведение обычных функций:
.
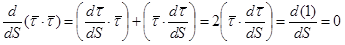Скалярное произведение двух векторов равно нулю, если эти векторы перпендикулярны. Таким образом:
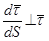или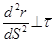 
. (2.20)
Прямая, по которой направлен вектор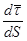 
, называется главной нормалью линии. Естественно, она расположена в нормальной плоскости (2.15) к линии.
Дата добавления: 2018-09-23; просмотров: 1236; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!