Дифференцируемость функции. Полный дифференциал
Возьмем полное приращение функции f(x, y) при перемещении из начальной точки P0(x0, y0) в какую-то точку 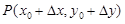 . Через
. Через 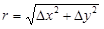 обозначим расстояние между P0 и P. Если приращению Dz при бесконечно малых Dx и Dy можно придать вид:
обозначим расстояние между P0 и P. Если приращению Dz при бесконечно малых Dx и Dy можно придать вид:
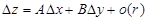 , (1.15)
, (1.15)
где A и B – постоянные числа, а o(r) (о малое) – бесконечно малое высшего порядка по сравнению с r, то функцию f(x, y) называют дифференцируемой в точке (x0, y0). Из (1.15) следует, что
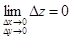 ,
,
т.е. дифференцируемая функция непрерывна.
Обратное утверждение неверно: из непрерывности дифференцируемость не вытекает.
Вычислим коэффициенты A и B. Положим Dy = 0. Тогда 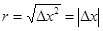 . Приращение Dz станет частным приращением Dx z:
. Приращение Dz станет частным приращением Dx z:
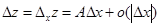 .
.
И мы имеем:
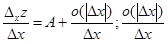 – бесконечно малая (б.м.),
– бесконечно малая (б.м.),
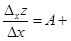 б.м.,
б.м., 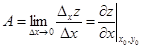 .
.
Точно так же получится, что 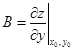 [надо взять Dx в формуле (1.15)]. Итак, если f(x, y) дифференцируема в (x0, y0), то она обладает обеими частными производными в этой точке и
[надо взять Dx в формуле (1.15)]. Итак, если f(x, y) дифференцируема в (x0, y0), то она обладает обеими частными производными в этой точке и
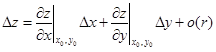 . (1.16)
. (1.16)
Выражение
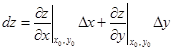 (1.17)
(1.17)
называется полным дифференциалом функции в точке (x0, y0). Оно линейно относительно произвольных приращений Dx и Dy независимых переменных и отличается от Dz на б.м. высшего порядка относительно r (и, значит, относительно Dx и Dy). Поэтому можно сказать, что дифференциал есть главная часть приращения функции, линейная относительно приращений независимых переменных. На приближенном равенстве
|
|
|
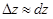 ,
,
которое тем точнее, чем меньше Dx и Dy, основано применение дифференциала в приближенных вычислениях (как и в случае функций одной переменной).
Если возьмем функцию z = x, то будем иметь
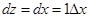 , так как
, так как 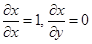 .
.
Таким образом, дифференциал независимого переменного x равен произвольному прира-щению x:
dx = Dx.
Точно таким же образом, рассмотрев функцию z = y, найдем, что dy = Dy и для дифференциала dz формулу (1.17) можно переписать так:
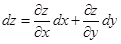 . (1.18)
. (1.18)
Мы опустили явное указание точки (x0, y0).
В случае функции одной переменной наличие производной и наличие дифференциала имело место одновременно и каждый из двух этих фактов влек название функции дифференцируемой. Для функции двух переменных из наличия дифференциала (именно в этом случае мы назвали функцию дифференцируемой) вытекает наличие частных производных. Однако из наличия частных производных не следует обязательно, как можно показать, дифференцируемости, т.е. формально выражение (1.18) написать можно, но оно не обязано отличаться от Dz на o(r), как требуется в (1.16).
Геометрический смысл полного дифференциала
Напишем уравнение касательной плоскости (1.14) в точке 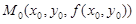 и сравним
и сравним
с (1.17). Если положим, как всегда, 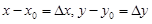 , то из (1.14) получаем:
, то из (1.14) получаем:
|
|
|
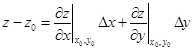 ,
,
а из (1.17), что это есть dz. Таким образом dz = z – z0, т.е. дифференциал есть приращение аппликаты точки, двигающейся по касательной плоскости, проведенной к поверхности в точке 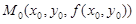 , и вызванное приращениями Dx и Dy независимых переменных. (В то время как Dz – приращение аппликаты точки, двигающейся по поверхности, и это приращение вызвано приращениями Dx и Dy аргументов.)
, и вызванное приращениями Dx и Dy независимых переменных. (В то время как Dz – приращение аппликаты точки, двигающейся по поверхности, и это приращение вызвано приращениями Dx и Dy аргументов.)
Обозначим через zП аппликату текущей точки на поверхности (рис. 7), а через zK – аппликату соответствующей ей (т.е. с такими же x и y) точки на касательной плоскости.
|
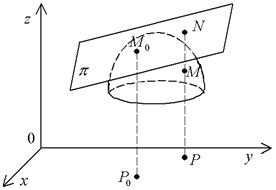
Рис. 7
Тогда 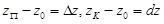 и из (1.16) получаем, что
и из (1.16) получаем, что 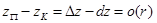 – б.м. высшего порядка.
– б.м. высшего порядка.
Этот факт означает теснейшее примыкание касательной плоскости к поверхности. Таким образом, в бесконечно малом можно “кривую” поверхность весьма точно заменить плоским “куском” – куском касательной плоскости.
Дата добавления: 2018-09-23; просмотров: 202; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

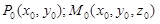 – точка касания;
– точка касания;
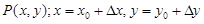 ;
;
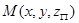 – точка поверхности;
– точка поверхности;
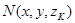 – точка касательной плоскости;
p – касательная плоскость
– точка касательной плоскости;
p – касательная плоскость