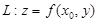Дифференцирование сложной функции
Пусть задана функция
z = f(u, v), (1.19)
но ее аргументы u и v сами являются функциями независимых переменных x и y:
z = f(u, v), u = j (x, y), v = y(x, y). (1.20)
Тогда
z = f(u, v) = f [j (x, y), y(x, y)] (1.21)
– сложная функция переменных x и y. Предполагаем все функции (1.20) дифференцируемыми. Дадим x б.м. приращение Dx. Тогда u, v, z получат соответствующие приращения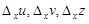 
. Имеем:
, 
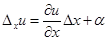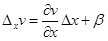, (1.22)
где a и b – б.м. высшего порядка относительно Dx. Приращения u и v вызовут приращение 
функции (1.19):
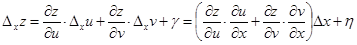. (1.23)
В (1.23) g – б.м. высшего порядка относительно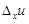 
и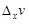 
, а h – как нетрудно показать – б.м. высшего порядка относительно Dx.
Из (1.23) получаем:
.
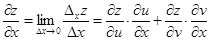Аналогично выводится формула для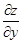 
. Выпишем эти формулы для дифференцирования сложной функции:
; (1.24)
.
Пример. 
. Положим xy = u, x – y = v. Тогда 
,
;
.
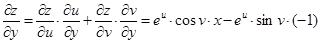
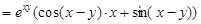Инвариантность формы записи дифференциала
Если бы в (1.19) u и v были независимыми переменными, то
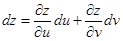. (1.25)
Однако независимыми переменными служат x и y и тогда
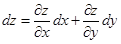. (1.26)
Из (1.20) получаем:
, 
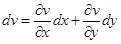. (1.27)
|
|
|
Используя (1.24) и (1.27), находим из (1.26)
,
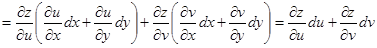т.е. форма полного дифференциала (1.25) не зависит от того, являются ли u и v независимыми переменными или функциями каких-то других аргументов.
Производные высших порядков
Возьмем 
и найдем ее частные производные по x и по y. Получим частные производные второго порядка: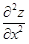 
, 
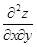(сначала дифференцируем по x, потом по y) (читается “дэ два зэт по дэ икс в квадрате”, “дэ два зэт по дэ икс, по дэ у”). Точно так же образуются
, 
.
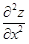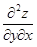Далее, дифференцируя производные второго порядка, можно образовывать производные третьего порядка: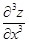 
, 
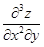(сначала два раза по x, затем по y), 
, 
, 
, 
, 
, 
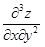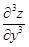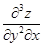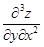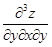. Другие обозначения 
, 
, 
, 
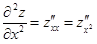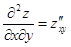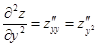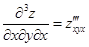и т.п.
Конечно, все это в предположении, что функция f(x, y) такова, что указанные дифференци-рования действительно возможны.
Оказывается, что результат повторного дифференцирования, если рассматриваемые произ-водные непрерывны, не зависит от порядка, в котором дифференцирование выполнялось, а только от количества сделанных по каждой из переменных дифференцирований, т.е.
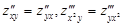и т.п.
Пример. 
; 
; 
;
; 
; 
; 
.
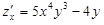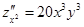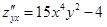Оказалось,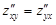 
.
Экстремумы функций двух переменных
Определение точек максимума и минимума для функции двух переменных дословно такое же, как для функций одной переменной. Следует лишь помнить, что теперь точка – это (x0, y0) (а не x0), а d-окрестность – круг радиуса d с центром в (x0, y0), а не интервал, содержащий x0. Поэтому мы воздержимся от повтора этих определений.
|
|
|
Необходимый признак экстремума
Если в точке экстремума (x0, y0) функция f(x, y) имеет частные производные, то они необходимо равны нулю:
, 
. (1.28)
Доказательство. Рассмотрим сечение поверхности z = f(x, y) плоскостью x = x0. На поверхности вырежется линия L – график функции одной переменной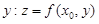 
. Функция от 
имеет в точке y0, т.е. в (x0, y0), экстремум того же характера, что и функция двух переменных f(x, y). Поэтому по необходимому признаку экстремума для функций одной переменной 
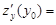
. Аналогично, рассматривая сечение y = y0, устанавливается другое из условий (1.28).
Геометрически (1.28) означает, что касательная плоскость p к поверхности в точке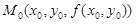 
, соответствующей точке экстремума (x0, y0), параллельна плоскости xOy (рис. 8).
|
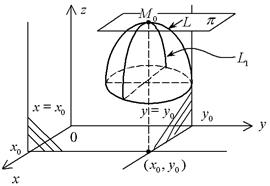
Рис. 8
Точки, в которых выполняются условия (1.28), называются стационарными; стационарные точки и точки, в которых нет по крайней мере одной из частных производных, – критическими. Именно такие точки “подозрительны” относительно наличия в них экстремума.
|
|
|
Дата добавления: 2018-09-23; просмотров: 180; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!