Функции двух переменных, непрерывность
Современная
Гуманитарная
Академия
Дистанционное образование
РУ.01;1
Рабочий учебник
Фамилия, имя, отчество обучающегося __________________________________________________
Направление подготовки ______________________________________________________________
Номер контракта _____________________________________________________________________
МАТЕМАТИЧЕСКИЙ АНАЛИЗ (КУРС 8)
Юнита 6
Дифференциальное и интегральное исчисление функций нескольких переменных
МОСКВА 2012
Разработано Е.А. Кошелевой, канд. техн. наук, доц.
Под ред. В.Н. Варапаева, д-ра физ.-мат. наук, проф.
Рекомендовано Учебно-методическим советом в качестве учебного пособия для студентов СГА
КУРС: МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Юнита 1. Элементы теории множеств и математической логики, функции.
Юнита 2. Предел и непрерывность функции одной переменной.
Юнита 3. Дифференциальное исчисление функций одной переменной.
Юнита 4. Интегральное исчисление функций одной переменной.
Юнита 5. Множество точек и последовательностей в n-мерном пространстве.
Юнита 6. Дифференциальное и интегральное исчисление функций нескольких переменных.
Юнита 7. Обыкновенные дифференциальные уравнения.
Юнита 8. Ряды. Ряды Фурье.
ЮНИТА 6
Изложены основные понятия и факты тем “Дифференциальное исчисление функций нескольких переменных”, “Приложения дифференциального исчисления к вопросам геометрии”, “Интегральное исчисление функций нескольких переменных, заданных в плоской или пространственной области (кратные интегралы), а также функций, заданных на кривых и поверхностях”.
|
|
|
Рабочий учебник составлен на основе дидактических единиц учебников, имеющих гриф Министерства образования и науки Российской Федерации или Учебно-методического объединения:
1. Ильин, В. А. Высшая математика [ЭР] : учебник для ВУЗов / В. А. Ильин, А. В. Куркина. - М. : Проспект, 2008.
2. Кудрявцев, Л. Д. Краткий курс математического анализа [ЭР] / Л. Д. Кудрявцев. - М. : Физматлит, 2005. Т. 2.
3. Кудрявцев, Л. Д. Математический анализ [Текст] : в 3 т / Л. Д. Кудрявцев. - М. : Дрофа, Т. 1, 2004. Т. 2, 2004, Т. 3, 2006.
Для студентов Современной Гуманитарной Академии
_____________________________________________________________________________________
© СОВРЕМЕННАЯ ГУМАНИТАРНАЯ АКАДЕМИЯ, 2012
(настоящее учебное пособие не может быть полностью или частично воспроизведено, тиражировано
и распространено в качестве официального издания без разрешения руководства СГА)
Соответствие системы менеджмента качества СГА в сфере создания информационных образовательных ресурсов требованиям международного стандарта ISO 9001:2000 (ГОСТ Р ИСО 9001-2001)
подтверждено Сертификатом соответствия Стандарт-тест
|
|
|
ОГЛАВЛЕНИЕ
Стр.
ДИДАКТИЧЕСКИЙ ПЛАН.. 5
ЛИТЕРАТУРА.. 6
ПЕРЕЧЕНЬ КОМПЕТЕНЦИЙ.. 7
Тематический обзор. 10
1. Функции нескольких переменных. Дифференциальное исчисление функций нескольких переменных.. 10
1.1. Функции двух переменных, непрерывность. 10
1.1.1. Функции двух переменных. 10
1.1.2. Области на плоскости. 10
1.1.3. Геометрическое изображение функции двух переменных. 11
1.1.4. Линии уровня. 12
1.1.5. Предел и непрерывность функции двух переменных. 12
1.1.6. Свойства непрерывных функций. 13
1.1.7. Приращения независимых переменных и приращение функции. 13
1.2. Дифференциальное исчисление функций двух переменных. 14
1.2.1. Частные производные. 14
1.2.2. Геометрический смысл частных производных. 15
1.2.3. Касательная плоскость к поверхности z = f(x, y) 15
1.2.4. Дифференцируемость функции. Полный дифференциал. 16
1.2.5. Геометрический смысл полного дифференциала. 17
1.2.6. Дифференцирование сложной функции. 18
1.2.7. Инвариантность формы записи дифференциала. 19
1.2.8. Производные высших порядков. 19
1.2.9. Экстремумы функций двух переменных. 20
1.2.10. Необходимый признак экстремума. 20
1.2.11. Достаточный признак экстремума. 21
1.2.12. Наибольшее и наименьшее значения в области. 21
|
|
|
1.3. Функции трех и более переменных. Скалярное поле. 22
1.3.1. Функция трех переменных. 22
1.3.2. Внутренние и граничные точки. 22
1.3.3. Поверхности уровня. 22
1.3.4. Функции любого числа переменных. 23
1.3.5. Предел, непрерывность, частные производные для функции нескольких переменных. 23
1.3.6. Касательная прямая и нормаль к графику неявной функции. 23
1.3.7. Касательная плоскость и нормаль к поверхности, заданной неявным уравнением.. 24
1.3.8. Скалярное поле. 24
1.3.9. Производная по направлению.. 24
1.3.10. Градиент скалярного поля. 26
2. Дополнительные вопросы приложений дифференциального исчисления к геометрии.. 27
2.1. Плоские кривые. Кривизна. 27
2.1.1. Дифференциал длины дуги. 27
2.1.2. Кривизна плоской линии. 29
2.1.3. Радиус кривизны. Круг и центр кривизны.. 30
2.2. Пространственные кривые. 31
2.2.1. Векторное уравнение пространственной кривой. 31
2.2.2. Касательная к пространственной кривой. 32
2.2.3. Нормальная плоскость. 33
2.2.4. Дифференциал длины дуги. 33
2.2.5. Натуральные уравнения кривой. Главная нормаль. 34
2.2.6. Кривизна пространственной кривой. 35
2.2.7. Соприкасающаяся плоскость. Бинормаль. Кручение. 36
2.2.8. Скорость и ускорение точки, движущейся по кривой. 36
2.2.9. О касательной плоскости к поверхности. 37
|
|
|
3. Кратные и криволинейные интегралы... 38
3.1. Определение кратного интеграла, условие существования и свойства кратного интеграла. 38
3.2. Сведение кратного интеграла к повторному. 41
3.3. Замена переменных в кратном интеграле. 44
3.4. Площадь поверхности. 47
3.5. Определение криволинейного интеграла, его свойства. 48
3.6. Формула Грина. 51
3.7. Определение поверхностного интеграла, его свойства. 51
3.8. Формула Стокса. 53
3.9. Формула Остроградского–Гаусса. 55
3.10. Соленоидальные и потенциальные векторные поля. 55
3.11. Геометрические и физические приложения кратных, криволинейных и поверхностных интегралов. 58
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ... 61
ТРЕНИНГ КОМПЕТЕНЦИЙ.. 67
ГЛОССАРИЙ.. 81
ДИДАКТИЧЕСКИЙ ПЛАН
Функция двух и нескольких переменных. Типы многомерных областей. Предел и непре-рывность. Полное и частное приращения. Частные производные. Касательная плоскость, ее уравнение. Дифференцируемость функций двух переменных. Полный дифференциал, его геоме-трический смысл, применение в приближенных вычислениях. Точки экстремума, необходимый и достаточный признаки.
Скалярное поле. Линии и поверхности уровня. Производная по направлению. Градиент и его свойства. Дальнейшие приложения дифференциального исчисления к геометрии. Кривизна плоских линий, круг кривизны и центр кривизны. Векторное уравнение пространственной кривой. Производная векторной функции как направляющий вектор касательной прямой. Кривизна пространственной кривой (как предел средней кривизны). Нормальная плоскость. Главная нормаль, бинормаль, кручение, соприкасающаяся плоскость (понятия).
Двойные и тройные интегралы, их определение, свойства и вычисление сведением к повторному. Замена переменных в кратных интегралах. Площадь поверхности. Механические приложения кратных интегралов: масса и центр тяжести неоднородного тела.
Криволинейный интеграл от вектор-функции, его определение, свойства и вычисление. Работа векторного поля. Формула Грина.
Поверхностный интеграл от вектор-функции, его определение, свойства, вычисление. Поток векторного поля.
Дифференциальные операции над скалярными и векторными полями: градиент скалярного поля, дивергенция и вихрь векторного поля. Формула Стокса. Формула Остроградского–Гаусса. Соленоидальные и векторные поля.
ЛИТЕРАТУРА *
1. Бугров, Я. С. Высшая математика [Текст] : в 3 т / Я. С. Бугров, С. М. Никольский. – М. : Дрофа, Т. 1, 2006. Т. 2, 2007. Т. 3, 2005. (Гриф МО РФ).
2. Данилов Ю. М., Журбенко Л. Н., Никонова Г. А., Никонова Н. В., Нуриева С. Н. Математика. Гриф МО РФ [Текст]: Учеб. пособие - ("Высшее образование") / Данилов Ю.М., Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-002673-2.
3. Ермаков В.И. Справочник по математике для экономистов. Гриф МО РФ [Текст]: Учебное пособие - 3-е изд., перераб. и доп. - ("Высшее образование") / Ермаков В.И. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-003542-0.
4. Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Дегтярева О.М. Математика в примерах и задачах. Гриф МО РФ [Текст]: Учеб. пособие - ("Высшее образование") / Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Дегтярева О.М. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-003449-2.
5. Ильин, В. А. Высшая математика [ЭР] : учебник для ВУЗов / В. А. Ильин, А. В. Куркина. - М. : Проспект, 2008. (с грифом УМО).
6. Клюшин В. Л. Высшая математика для экономистов. Гриф МО РФ [Текст]: Учеб. пособие - ("Учебники РУДН") / Клюшин В.Л. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-002752-4.
7. Кудрявцев, Л. Д. Краткий курс математического анализа [ЭР] / Л. Д. Кудрявцев. - М. : Физматлит, 2005. Т. 2. (с грифом УМО) Электронная библиотека "Мир книг" (www.mirknig.su).
8. Кудрявцев, Л. Д. Математический анализ [Текст] : в 3 т / Л. Д. Кудрявцев. - М. : Дрофа,
Т. 1, 2004. Т. 2, 2004, Т. 3, 2006. (с грифом МО РФ).
9. Кузнецов, Б. Т. Математика [Текст] : учебник для студентов вузов, обучающихся по специальностям экономики и управления / Б. Т. Кузнецов. - 2-е изд., перераб. и доп. - М. : ЮНИТИ-ДАНА, 2004. - 719 с. - ISBN 5-238-00754-Х.
10. Малыхин В. И. Высшая математика. Гриф МО РФ [Текст]: Учебное пособие - 2-е изд., перераб. и доп. - ("Высшее образование") / Малыхин В.И. - М.: ИНФРА-М,-2009. - ISBN: 5-16-002625-8.
11. Пискунов, Н. С. Дифференциальные и интегральные исчисления [Текст] : в 2 т /
Н. С. Пискунов. – М. : Интеграл-Пресс, 2007. (Гриф МО РФ).
12. Фихтенгольц, Г. М. Курс дифференциального и интегрального исчисления [Текст] : в 3 т / Г. М. Фихтенгольц. - М. : Физматлит, Т. 1, 2007. Т. 2 , 206. Т. 3, 2008. (Гриф МО РФ).
ПЕРЕЧЕНЬ КОМПЕТЕНЦИЙ
| № п/п | Умение | Алгоритм |
| 1 | Вычисление частных производных первого и второго порядков функ-ций двух переменных | 1. Вычислить первые производные:
а) считая y постоянным, дифференцируем функцию y = f(x) по переменному x – находим частную производную 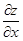 по x;
б) частную производную по y – по x;
б) частную производную по y – 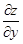 находим аналогично, фиксируя x.
2. Вычислить вторые производные находим аналогично, фиксируя x.
2. Вычислить вторые производные 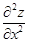 и и 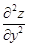 :
а) считая y постоянным, дифференцируем :
а) считая y постоянным, дифференцируем 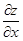 по переменному x – получаем по переменному x – получаем 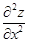 ;
б) считая x постоянным, дифференцируем ;
б) считая x постоянным, дифференцируем 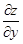 по переменному y – получаем по переменному y – получаем 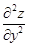 .
3. Вычислить смешанные производные:
а) считая x постоянным, дифференцируем .
3. Вычислить смешанные производные:
а) считая x постоянным, дифференцируем 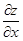 по переменному y – находим по переменному y – находим 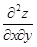 ;
б) считая y постоянным, дифференцируем ;
б) считая y постоянным, дифференцируем 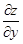 по переменному x – находим по переменному x – находим 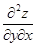 ;
в) сравнивая полученные производные, убеждаемся, что ;
в) сравнивая полученные производные, убеждаемся, что 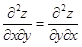
|
| 2 | Записать уравнение каса-тельной плоскости и найти полный диффе-ренциал функции в точке | 1. Вычислить частные производные 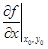 и и 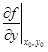 и и 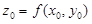 .
2. Подставить полученные значения в уравнение касательной плоскости .
2. Подставить полученные значения в уравнение касательной плоскости
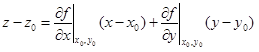 .
3. Найти полный дифференциал .
3. Найти полный дифференциал
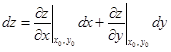
|
| № п/п | Умение | Алгоритм |
| 3 | Нахождение экстремума функции двух перемен-ных | 1. Найти область определения.
2. Найти частные производные 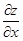 и и 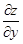 .
3. Найти точки, в которых .
3. Найти точки, в которых 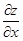 и и 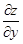 равны нулю или не существуют, т.е. критические точки (необходимое условие наличия экстремума).
4. Найти равны нулю или не существуют, т.е. критические точки (необходимое условие наличия экстремума).
4. Найти 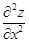 , , 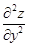 , , 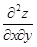 .
5. Вычислить значения частных производных второго порядка в критических точках.
6. Использовать достаточное условие наличия экстремума. Составить .
5. Вычислить значения частных производных второго порядка в критических точках.
6. Использовать достаточное условие наличия экстремума. Составить
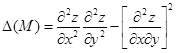 и вычислить его значения в критических точках Mk (k = 0,1,2,3…).
7. Сделать вывод о наличии экстремума:
и вычислить его значения в критических точках Mk (k = 0,1,2,3…).
7. Сделать вывод о наличии экстремума:
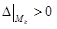 – экстремум есть; – экстремум есть;
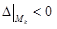 – нет экстремума; – нет экстремума;
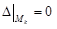 – неопределенный случай, требующий дополнитель-ного исследования.
8. По знаку второй производной в точке M0 установить характер экстремума:
а) – неопределенный случай, требующий дополнитель-ного исследования.
8. По знаку второй производной в точке M0 установить характер экстремума:
а) 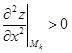 – точка минимума;
б) – точка минимума;
б) 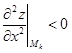 – точка максимума.
9. Вычислить экстремальное значение функции. – точка максимума.
9. Вычислить экстремальное значение функции.
|
| 4 | Вычисление наиболь-шего и наименьшего значений функции в замкнутой области | 1. Сделать чертеж области D. 2. Найти стационарные точки, лежащие внутри D. 3. Исследовать функцию на границе области. Подставить в функцию уравнение границы и найти наименьшее и наиболь-шее значения полученной функции одной переменной – параметра, к которому отнесены линии, ограничивающие область D. 4. Сравнить все вычисленные значения функции в отдельных точках и найти среди них наименьшее и наибольшее, которые и будут соответственно наименьшим и наибольшим значением функции в области D. |
| 5 | Вычисление производ-ной по направлению и градиента скалярного поля (для функций двух или трех переменных) | 1. Вычислить частные производные функции u = f(x, y, z) по переменным x, y, z в точке P0(x0, y0, z0).
2. Вычислить градиент функции u = f(x, y, z) в точке P0(x0, y0, z0) по формуле:
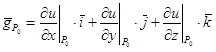
|
| № п/п | Умение | Алгоритм |
3. Вычислить производную по направлению 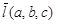 в точке P0(x0, y0, z0): в точке P0(x0, y0, z0):
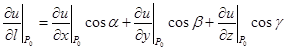 ;
направляющие косинусы ;
направляющие косинусы 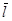 находятся по формуле: находятся по формуле: 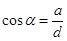 , , 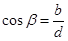 , , 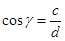 , где , где 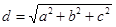 , ,
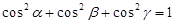 .
Примечание: В случае двух переменных применяем анало-гичные формулы: .
Примечание: В случае двух переменных применяем анало-гичные формулы:
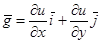 , , 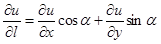 ,
где теперь ,
где теперь 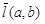 , , 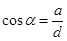 , , 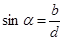 , , 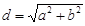 . .
| ||
| 6 | Написать уравнения ка-сательной плоскости и нормали к поверхности, заданной неявным урав-нением F(x, y, z) = 0 | 1. Вычислить 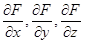 и подставить в них координаты (x0, y0, z0) заданной точки.
2. Записать уравнение касательной плоскости: и подставить в них координаты (x0, y0, z0) заданной точки.
2. Записать уравнение касательной плоскости:
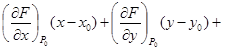 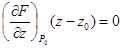 .
3. Записать уравнение нормали: .
3. Записать уравнение нормали:
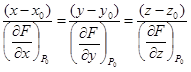 . .
|
| 7 | Написать уравнения каса-тельной прямой и нор-мальной плоскости к пространственной кри-вой, заданной параме-трически:
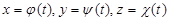
| 1. Определить значение параметра t0, соответствующее задан-ной точке (x0, y0, z0) на кривой.
2. Если задано значение t0 параметра, то найти точку
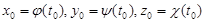 .
3. Записать уравнение касательной прямой: .
3. Записать уравнение касательной прямой:
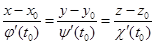 .
4. Записать уравнение нормальной плоскости: .
4. Записать уравнение нормальной плоскости:
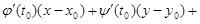 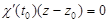 . .
|
| 8 | Вычисление двойного интеграла в декартовых координатах | 1. Нарисовать область интегрирования. 2. Представить двойной интеграл в виде повторного, определив порядок интегрирования и расставив пределы интегрирования. 3. Вычислить повторный интеграл. |
Тематический обзор *
1. Функции нескольких переменных. Дифференциальное
исчисление функций нескольких переменных
Функции двух переменных, непрерывность
Функции двух переменных
Пусть на плоскости xOy имеется некоторое множество точек D. Пусть каждой точке PÎD поставлено в соответствие по некоторому правилу число z: P®z. Тогда говорят, что на множестве D задана функция z = f(P). Аргументом этой функции служит геометрический объект: точка P, пробегающая множество D, а значением – величина (переменная) z. Однако положение каждой точки P определяется парой ее координат x и y: P(x,y). Координаты этой точки независимы друг от друга и поэтому можно сказать, что задана функция z = f(x,y) двух независимых переменных x и y.
Итак, переменная величина z называется функцией двух независимых переменных x и y:
z = f(x, y) (или функцией точки P(x, y): z = f(P)), заданной на некотором множестве D, если по какому-то закону или правилу каждой паре x, y Î D (каждой точке PÎD) соответствует определенное значение z. Множество D называется областью определения функции. Множество значений z, принимаемых функцией z = f(P), когда P пробегает множество D, составляет область значений функции.
Пример. Пусть x и y – стороны прямоугольника, z – его площадь. Тогда z = xy – функция двух независимых переменных x и y, заданная на множестве 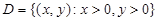 (рассматриваем только невырожденные прямоугольники) – это первый квадрант плоскости xOy. Множеством значений z будет интервал (0, +∞).
(рассматриваем только невырожденные прямоугольники) – это первый квадрант плоскости xOy. Множеством значений z будет интервал (0, +∞).
Здесь область определения функции вытекала из конкретного смысла величин x и y. Закон же соответствия z = xy никаких ограничений не диктует и если бы мы не знали конкретного смысла x и y в этой задаче, то областью определения надо было считать всю плоскость xOy.
Области на плоскости
Для функций y = f(x) одной переменной в качестве области определения чаще всего выступали интервалы. Как обстоит дело для функций нескольких переменных? Назовем d-окрестностью точки (x0, y0) множество точек внутри круга радиуса d (d > 0) с центром в (рис. 1). (Окружность круга к окрестности не относим.)
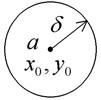
Рис. 1
Точка (x0, y0) называется внутренней для множества D, если она принадлежит D вместе с некоторой своей d-окрестностью. Открытой областью назовем такое множество, что 1) любые его точки – внутренние и 2) любые две его точкиможно соединить непрерывной линией,
лежащей в D (рис. 2).
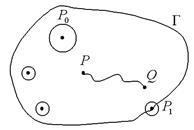
Рис. 2
Заметим, что радиусы d-окрестностей различных точек D различны. Чаще всего область – это часть плоскости, лежащая внутри замкнутого контура Г. Точка P1 называется граничной для области D, если в любой d-окрестности этой точки есть как точки из D, так и точки, не принадлежащие D. Совокупность всех граничных точек составляет границу области (на рис. 2 это контур Г). Если к открытой области D присоединить ее границу Г, то получается замкнутая область 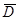 .
.
В качестве области определения для функций двух переменных чаще всего выступают открытые или замкнутые области. Область D – ограниченная, если ее можно поместить в какой-нибудь круг. В примере из раздела 1.1.1 – неограниченная область.
Дата добавления: 2018-09-23; просмотров: 205; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
