Кривизна пространственной кривой
Найдем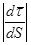 
. Перейдем из начального положения M (дуговая координата S) в положение M1 (дуговая координата S + DS). Касательный вектор 
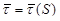в M перейдет в касательный вектор 
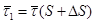точки M1. Таким образом, произошел поворот касательного вектора (рис. 23) на угол Da; этот угол называют углом смежности (чтобы обозначить этот угол, вектор 
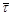перено-сится в точку M1).
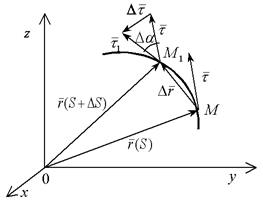
Рис. 23
Происшедший поворот касательного вектора 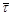характеризует изогнутость кривой (будь она прямой линией, было бы Da = 0). Отношение 
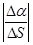называется (как и в случае плоской кривой) средней кривизной кривой на участке DS:
.
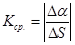Предел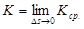 
называется кривизной кривой в точке M:
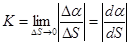. (2.21)
Следовательно, кривизна – это скорость изменения угла смежности касательных относи-тельно длины дуги.
Треугольник со сторонами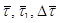 
– равнобедренный, так как 
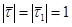и имеет угол при вершине Da. Из этого треугольника находим: 
. Вычисляем предел:
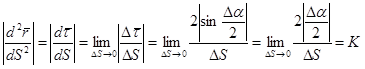. (2.22)
Таким образом, вектор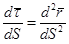 
направлен по главной нормали и имеет модуль, равный кривизне. Величину, обратную K, называют, как и в плоском случае, радиусом кривизны R:
. (2.23)
Если обозначить орт (единичный вектор) главной нормали через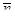 
, то
. (2.24)
В случае, когда кривая задана параметрическими уравнениями (2.11), формула для кривизны K имеет более сложный вид, чем (2.22) (см. [2]).
|
|
|
Соприкасающаяся плоскость. Бинормаль. Кручение
Плоскость, содержащая касательную прямую и главную нормаль, называется соприка-сающейся плоскостью кривой L (в данной точке). Можно показать, что соприкасающаяся плоскость кривой L в точке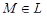 
получается следующим образом. Возьмем три точки M1, M, M2 на L и проведем через них плоскость Q. Пр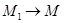и 
и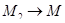 
, т.е. когда эти три точки стремятся слиться в точке M, плоскость Q стремится занять некоторое предельное положение. Это предельное положение и есть соприкасающаяся плоскость к L в точке M. Если кривая плоская, то соприкасающаяся плоскость в любой ее точке та, в которой лежит кривая. Если при переходе от точки M к точке M1 на кривой двугранный угол между соприкасающимися плоскостями в M и M1 есть Db, то дробь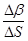 
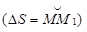показывает меру отличия изучаемой пространственной кривой от плоской на участке DS.
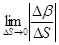(2.25)
называется кручением кривой в точке M. Кручение характеризует отличие пространственной линии от плоской, в то время как кривизна – отличие линии от прямой (все в данной точке M). Если возьмем векторное произведение
|
|
|
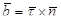(2.26)
ортов касательной 
и главной нормали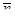 
, то получим орт бинормали. Бинормаль перпендикулярна и касательной, и главной нормали и, значит, перпендикулярна соприкасающейся плоскости. Лежит бинормаль в нормальной плоскости.
Угол Db из (2.25) может быть измерен как угол между двумя положениями бинормали: в M и M1 (подробно см. [2]).
Дата добавления: 2018-09-23; просмотров: 264; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!