Радиус кривизны. Круг и центр кривизны
Величина
(2.10)
называется радиусом кривизны в соответствующей точке. Это естественно, поскольку именно так обстоит дело с окружностью
Если по нормали к кривой L отложить R в сторону вогнутости кривой, то получится центр кривизны C (рис. 19).
Рис. 19
Окружность, очерченная из C радиусом R, называется кругом (окружностью) кривизны. Можно доказать, что окружность кривизны есть предельное положение окружности, проведенной через 3 точки M1, M0, M2 на кривой, когда эти точки сливаются в одну M0, т.е. когда M1 ® M0,
M2 ® M0. Поэтому в некотором смысле бесконечно малая дуга окружности кривизны еще теснее заменяет бесконечно малую дугу кривой, чем бесконечно малый отрезок касательной прямой: ведь касательная – это предельное положение секущей, а у секущей лишь две общие с кривой точки.
Если построение центров кривизны провести для всех точек данной линии, то совокупность этих центров составит новую кривую, которая для первоначальной называется ее эволютой, а заданная первоначальная кривая по отношению к своей эволюте называется ее эвольвентой (более подробно эти вопросы см. [2], гл. VI, §§6–7).
Пространственные кривые
Векторное уравнение пространственной кривой
Кривая линия в пространстве может быть задана как пересечение двух поверхностей:
F(x, y, z) = 0;
F(x, y, z) = 0.
Например, линия
|
|
|
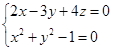
есть эллипс, получающийся от среза прямого кругового цилиндра (второе уравнение) плоскостью (первое уравнение).
Более удобным во многих вопросах является задание линии параметрическими уравнениями:
. (2.11)
Координаты x, y, z текущей по кривой точки задаются как функции от параметра t, меняющегося на каком-то интервале. Например, линию из предыдущего примера можно задать такими уравнениями:
.
Первые два из этих уравнений на плоскости xOy изображают окружность, а в пространстве дают координаты x и y любой точки на цилиндрической поверхности, основанием которой служит эта окружность, координата z найдена из уравнения плоскости.
Рассмотрим в пространстве вектор
( 
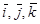– орты) (2.12)
с переменными координатами x, y и z. Мы сталкиваемся здесь с новым видом функциональной зависимости: аргументом этой функции является обычная переменная величина t, а значением функции – переменная векторная величина. Обычная величина t характеризуется только своими численными значениями, но значения переменной векторной величины – это векторы, а векторы характеризуются не только своими размерами, но и направлением. Когда в одном описании одновременно встречаются и обычные, и векторные величины, то обычные величины именуют скалярными и тем отличают от векторных. Мы уже встречались с переменными векторными величинами, когда в разделе 1.3 рассматривали поле градиента скалярной функции.
|
|
|
Векторная функция (2.12) задает нашу пространственную линию и служит заменой параметрических уравнений (2.11) этой линии (рис. 20).
Рис. 20
При изменении t конец вектора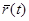 
(этот вектор называют радиус-вектором) описывает кривую. И эта кривая служит изображением функции 
. Ее называют годографом этой функции.
Дата добавления: 2018-09-23; просмотров: 358; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!