Достаточный признак экстремума

 

Пусть в некоторой внутренней точке (x₀, y₀) области D функция f(x, y) имеет непрерывные частные производные до третьего порядка включительно.

Если выполнены равенства (1.28) и выражение

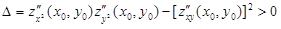,                                   (1.29)

то в точке (x₀, y₀) – экстремум. При этом если наряду с (1.28) и (1.29) еще ,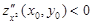
то в (x₀, y₀) – максимум, а если 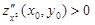, то в(x₀, y₀) – минимум.

Если же выполнены условия (1.28), но D < 0, то экстремума нет. В случае, когда D = 0, экстремум может быть, а может и не быть – здесь наш признак “молчит”.

Доказательство опустим.

 

 

Наибольшее и наименьшее значения в области

 

Наибольшее и наименьшее значения функции, непрерывной в ограниченной замкнутой области, существуют. Где их искать? Среди критических точек внутри области, но они могут также оказаться и среди граничных точек.

Пример. Найти наибольшее значение функции z = (1 – x – y)xy в области D: x ³ 0, y ³ 0,
2 – x – y ³ 0 (рис. 9).

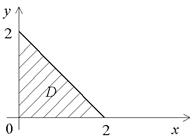
Рис. 9

Область ограничена осями координат и прямой x + y = 2; она замкнута.

Стационарные точки:

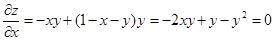
2x + y = 1;

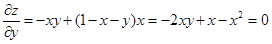
x + 2 y = 1.

Решаем систему:

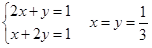 – стационарная точка.

Исследование на границе: x = 0, z = 0, y = 0, z = 0; x + y = 2, 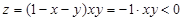. Таким образом, на границе z либо равно 0, либо принимает отрицательные значения. Значит, наибольшее значение – в стационарной точке и оно равно .

 

 

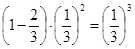Функции трех и более переменных. Скалярное поле

Функция трех переменных

 

Пусть D – некоторое множество точек в трехмерном пространстве. Если каждой точке P Î D поставлено в соответствие по некоторому правилу число u: P ® u, то на множестве D задана функция u = f(P). Аргумент этой функции – точка P, значение – переменная величина u. Поскольку каждая точка P определяется тремя координатами x, y, z: P(x, y, z), то u есть функция трех независимых переменных, заданная на множестве D:

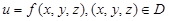,                                               (1.30)

где D – область определения функции f.

Пример. u – объем параллелепипеда со сторонами x, y, z: u = xyz. Функция задана на множестве точек (x, y, z), у которых 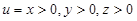. Область определения D этой функции – первый октант пространства.

 

 

Внутренние и граничные точки

 

Определяются дословно так же, как в случае двух переменных, но теперь d-окрестность
точки x₀, y₀, z₀ – это внутренность шара радиуса d с центром (x₀, y₀, z₀).

 

 

Поверхности уровня

 

Если задана функция u = f(x, y, z), то множество точек, в которых она принимает одно и то же значение C, – множество уровня (уровня C); обычно это поверхность уровня. Ее уравнение:

f(x, y, z) = C.                                                           (1.31)

Давая С различные значения, получаем семейство поверхностей уровня, дающее опреде-ленное представление о некоторых свойствах функции.

Пример. 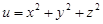. Поверхности уровня 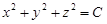,  – это сферы радиуса . При С = 0 сфера вырождается в точку – начало координат.

 

 

Функции любого числа переменных

 

Задано некоторое множество D “объектов” P, каждый из которых является каким-то набором из n чисел: P(x₁,…,x_n). Такие объекты трактуются как точки n-мерного пространства Rⁿ
(R³ – обычное трехмерное пространство, R² – плоскость, R¹ = R – числовая ось). Вводится расстояние в Rⁿ между любыми двумя точкам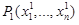и  и :

.

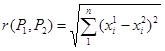Определяется d-окрестность точки P₀ – это множество всех точек P, для которых r(P, P₀) < d. После этого понятия внутренней или граничной точки множества D, открытой и замкнутой области описываются дословно так же, как в R² и R³.

Если каждой точке P из множества D, лежащего в Rⁿ, поставлено в соответствие по некоторому правилу число u: P ® u, то на множестве D задана функция точки P: u = f(P). Поскольку каждая точка определяется набором своих координат, то u = f(x₁,…x_n) – функция n независимых переменных. Множество D – область определения этой функции.

Пример. 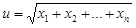; D – состоит из точек P, для которых сумма координат ³ 0.

 

 

---

Дата добавления: 2018-09-23; просмотров: 193; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!