Геометрическое изображение функции двух переменных
Пусть в области D задана функция z = f(P). Поставим в каждой точке PÎD “столбик” высотой z = f(P) (откладываем z по оси Oz – оси аппликат). В результате над областью D “натянется крыша” – поверхность, опирающаяся на все построенные “столбики” (рис. 3).
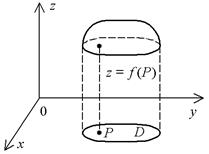
Рис. 3
Конечно, некоторые части этой “крыши” окажутся не над D, а под D, если в соответствующих точках у функции отрицательные значения. Эта поверхность и есть геометрическое изображение функции z = f(P) = f(x, y). Уравнение z = f(x, y), связывающее три координаты (x, y, z) точек поверхности, – уравнение этой поверхности.
Пример. z = x2 + y2 – параболоид вращения (рис. 4).
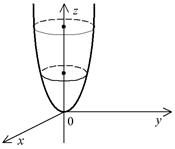
Рис. 4
Линии уровня
Возьмем какое-либо значение z = C из области значений функции z = f(x, y). Совокупность точекна плоскости xOy, в которых принимается это значение, будет называться множеством уровня (уровня C). Чаще всего это линия, линия уровня C. Получается эта линия как проекция на плоскость xOy линии пересечения поверхности z = f(x, y) с горизонтальной плоскостью z = C (рис. 5).
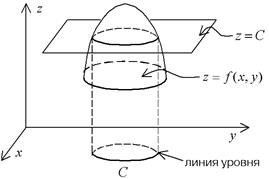
Рис. 5
Для поверхности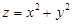 
из предыдущего примера линиями уровня будут окружности 
, 
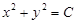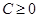. При C = 0 окружность выродится в точку (0, 0). Нанеся на плоскость xOy достаточно частую сетку линий уровня, у каждой из которых проставлен ее уровень C, получим достаточно ясное представление о рельефе поверхности z = f(x, y). Этим часто пользуются в топографии: здесь, конечно, уравнение поверхности (холмов, впадин и т.п.) отсутствует, но из непосредственных измерений строится сетка линий уровня изучаемого рельефа, и эта сетка дает плоское изображение пространственного рельефа данной местности.
|
|
|
Предел и непрерывность функции двух переменных
Пусть функция f(P) = f(x, y) определена в некоторой области D, а точка P0 – либо точка этой области, либо граничная для D; в самой точке P0 функция может быть и не определена (если D – открытая область и P0 лежит на ее границе). В соответствии с общими взглядами на предел приходим к такому определению: число a есть предел функции f(P) при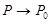 
(или в точке P0), если для 
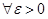найдется d > 0 такое, что во всех точках P (кроме, быть может, самой точки P0) области D, попавших в d-окрестность точки P0, выполняется неравенство:
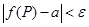. (1.1)
То же самое в символической записи:
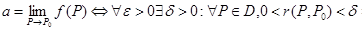
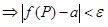, (1.2)
где r(P, P0) – расстояние от P до P0.
Аналогичным образом можно определить, что означает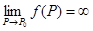 
.
Если теперь f(P) определена в замкнутой области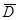 
, то она непрерывна в точке 
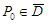(неважно, внутренней или граничной), если
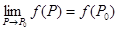. (1.3)
Точки, в которых условие непрерывности (1.3) нарушено, называются точками разрыва. Для функций двух переменных точки разрыва могут заполнять целые линии.
|
|
|
Примеры.
1. 
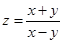. Функция определена во всех точках (x, y), у которых x ¹ y. На прямой y = x она не определена и поэтому эта прямая состоит из точек разрыва функции.
2. 
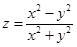. Функция определена всюду, кроме точки (0, 0). Покажем, что 
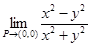не существует. Действительно, если P(x, 0) движется по оси абсцисс, то 
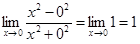. Если же 
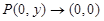по оси ординат, то 
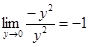. Таким образом, ни для какого a угодить условию (1) невозможно.
3. Функция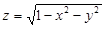 
определена всюду в замкнутом круге 
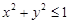и, как можно проверить, опираясь на обычные свойства предела, непрерывна в этом круге.
Свойства непрерывных функций
Для свойств непрерывных на замкнутом интервале функций также справедливы утверждения: если f(x, y) непрерывна в замкнутой, ограниченной области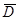 
, то она: 1) достигает там своего наибольшего и наименьшего значений; 2) ограничена; 3) принимает все значения, промежуточные между наименьшим и наибольшим.
Дата добавления: 2018-09-23; просмотров: 285; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!