ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Составьте логическую схему базы знаний по теме юниты:
2. Решите самостоятельно следующие задачи:
Вариант 1
1. Найти область определения функции  .
.
2. Построить линии уровня функции z = x + y.
3. Вычислить частные производные первых и вторых порядков функции двух переменных 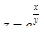 .
.
4. Вычислить полный дифференциал функции  в точке
в точке  .
.
5. Исследовать на экстремум функцию  .
.
6. Найти наибольшее и наименьшее значения функции  в прямоугольнике, ограниченном прямыми x = –1, x = 1, y = 0, y = 2.
в прямоугольнике, ограниченном прямыми x = –1, x = 1, y = 0, y = 2.
7. Найти градиент функции 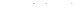 в точке
в точке 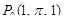 .
.
8. Найти производную функции  в направлении вектора
в направлении вектора  в точке
в точке  .
.
9. Написать уравнение нормали к эллипсоиду 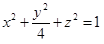 в точке
в точке 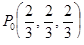 .
.
10. Вычислить двойной интеграл 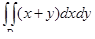 , где D – область, ограниченная линиями y = x, y = 1, x = 0.
, где D – область, ограниченная линиями y = x, y = 1, x = 0.
Вариант 2
1. Найти область определения функции  .
.
2. Построить линии уровня функции 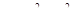 .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных  .
.
4. Вычислить полный дифференциал функции 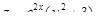 в точке
в точке 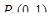 .
.
5. Исследовать на экстремум функцию 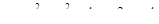 .
.
6. Найти наибольшее и наименьшее значения функции  в прямоугольнике, ограниченном прямыми x = 0, x = 2, y = –1, y = 1.
в прямоугольнике, ограниченном прямыми x = 0, x = 2, y = –1, y = 1.
7. Найти градиент функции  в точке
в точке 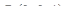 .
.
8. Найти производную функции 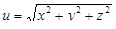 в направлении вектора
в направлении вектора  в точке
в точке 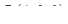 .
.
9. Провести нормальную плоскость к кривой  в точке
в точке 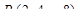 .
.
10. Вычислить двойной интеграл 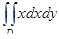 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 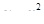 ,
, 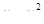 .
.
Вариант 3
|
|
|
1. Найти область определения функции 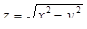 .
.
2. Построить линии уровня функции  .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных 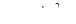 .
.
4. Вычислить полный дифференциал функции 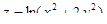 в точке
в точке  .
.
5. Исследовать на экстремум функцию 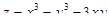 .
.
6. Найти наибольшее и наименьшее значения функции 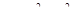 в круге
в круге 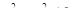 .
.
7. Найти градиент функции 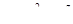 в точке
в точке  .
.
8. Найти производную функции  в направлении вектора
в направлении вектора  в точке
в точке 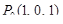 .
.
9. Провести касательную прямую к кривой 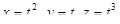 при t = 2.
при t = 2.
10. Вычислить двойной интеграл 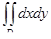 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 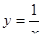 , y = x, y = 4x(x > 0).
, y = x, y = 4x(x > 0).
Вариант 4
1. Найти область определения функции  .
.
2. Построить линии уровня функции  .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных  .
.
4. Вычислить полный дифференциал функции  в точке
в точке  .
.
5. Исследовать на экстремум функцию 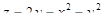 .
.
6. Найти наибольшее и наименьшее значения функции 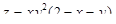 в треугольнике x = 0, y = 0, y + x = 6.
в треугольнике x = 0, y = 0, y + x = 6.
7. Найти градиент функции  в точке
в точке  .
.
8. Найти производную функции  в направлении биссектрисы первого коорди-натного угла в точке
в направлении биссектрисы первого коорди-натного угла в точке 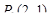 .
.
9. Провести касательную прямую к винтовой линии x = cos t, y = sin t, z = t в точке, отвечающей значению 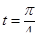 .
.
10. Вычислить двойной интеграл 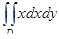 , где D – область, ограниченная линиями y = x, x = 0, y = 1.
, где D – область, ограниченная линиями y = x, x = 0, y = 1.
|
|
|
Вариант 5
1. Найти область определения функции 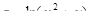 .
.
2. Построить линии уровня функции 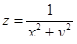 .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных 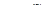 .
.
4. Вычислить полный дифференциал функции 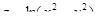 в точке
в точке 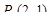 .
.
5. Исследовать на экстремум функцию 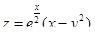 .
.
6. Найти наибольшее и наименьшее значения функции 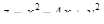 в прямоугольнике, ограниченном прямыми x = 1, x = 3, y = –1, y = 1.
в прямоугольнике, ограниченном прямыми x = 1, x = 3, y = –1, y = 1.
7. Найти градиент функции 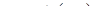 в точке
в точке 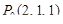 .
.
8. Найти производную функции 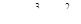 в направлении вектора
в направлении вектора  в точке
в точке  .
.
9. Провести касательную плоскость к поверхности  в точке
в точке 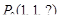 .
.
10. Вычислить двойной интеграл 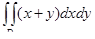 , где D – область, ограниченная линиями y = x2, x = 2, y = 0.
, где D – область, ограниченная линиями y = x2, x = 2, y = 0.
Вариант 6
1. Найти область определения функции 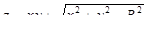 .
.
2. Построить линии уровня функции 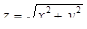 .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных  .
.
4. Вычислить полный дифференциал функции 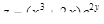 в точке
в точке 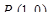 .
.
5. Исследовать на экстремум функцию 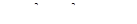 .
.
6. Найти наибольшее и наименьшее значения функции 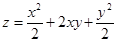 в прямоугольнике, ограниченном прямыми x = –1, x = 1, y = –1, y = 1.
в прямоугольнике, ограниченном прямыми x = –1, x = 1, y = –1, y = 1.
7. Найти градиент функции  в точке
в точке 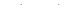 .
.
8. Найти производную функции  в направлении вектора
в направлении вектора 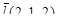 в точке
в точке  .
.
9. Написать уравнение нормали к поверхности 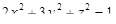 в точке
в точке  .
.
|
|
|
10. Вычислить двойной интеграл 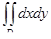 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 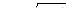 ,
,
y = –2x – 3, y = 3.
Вариант 7
1. Найти область определения функции 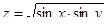 .
.
2. Построить линии уровня функции 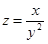 .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных  .
.
4. Вычислить полный дифференциал функции 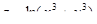 в точке
в точке 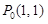 .
.
5. Исследовать на экстремум функцию 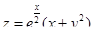 .
.
6. Найти наибольшее и наименьшее значения функции 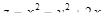 в прямоугольнике, ограниченном прямыми x = –3, x = 0, y = 1, y = –1.
в прямоугольнике, ограниченном прямыми x = –3, x = 0, y = 1, y = –1.
7. Найти градиент функции 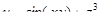 в точке
в точке  .
.
8. Найти производную функции 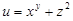 в направлении вектора
в направлении вектора 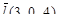 в точке
в точке  .
.
9. Написать уравнение касательной плоскости к поверхности 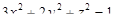 в точке
в точке  .
.
10. Вычислить двойной интеграл 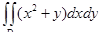 , где D – область, ограниченная линиями x2 = y, x = 0, y = 1.
, где D – область, ограниченная линиями x2 = y, x = 0, y = 1.
Вариант 8
1. Найти область определения функции 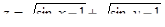 .
.
2. Построить линии уровня функции 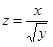 .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных
z = cos(xy).
4. Вычислить полный дифференциал функции 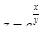 в точке
в точке  .
.
5. Исследовать на экстремум функцию 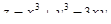 .
.
6. Найти наибольшее и наименьшее значения функции 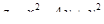 в прямоугольнике, ограниченном прямыми x = –1, x = 1, y = 0, y = 4.
в прямоугольнике, ограниченном прямыми x = –1, x = 1, y = 0, y = 4.
7. Найти градиент функции 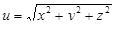 в точке
в точке  .
.
8. Найти наибольшую скорость возрастания функции z = x2 – 2 xy + 3y при переходе через точку P0 (1, 2).
|
|
|
9. Провести касательную прямую к плоской линии, заданной уравнением 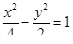 в точках (4,?).
в точках (4,?).
10. Вычислить двойной интеграл  , где D – область, ограниченная линиями y = 0, x = 2,
, где D – область, ограниченная линиями y = 0, x = 2, 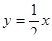 .
.
Вариант 9
1. Найти область определения функции 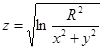 .
.
2. Построить линии уровня функции  .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных  .
.
4. Вычислить полный дифференциал функции  в точке
в точке  .
.
5. Исследовать на экстремум функцию  .
.
6. Найти наибольшее и наименьшее значения функции  в прямоугольнике, ограниченном прямыми x = 1, x = –1, y = 0, y = 5.
в прямоугольнике, ограниченном прямыми x = 1, x = –1, y = 0, y = 5.
7. Найти градиент функции 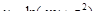 в точке
в точке  .
.
8. Найти наибольшую скорость возрастания функции 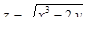 при переходе через точку
при переходе через точку  .
.
9. Провести нормальную плоскость к кривой x = t, y = t2, z = –t3 в точке (1,1, –1).
10. Вычислить двойной интеграл 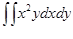 , где D – область, ограниченная линиями y = 4 – x2, x – y + 2 = 0.
, где D – область, ограниченная линиями y = 4 – x2, x – y + 2 = 0.
Вариант 10
1. Найти область определения функции 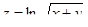 .
.
2. Построить линии уровня функции  .
.
3. Вычислить частные производные первых и вторых порядков функции двух переменных 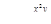 .
.
4. Вычислить полный дифференциал функции  в точке
в точке  .
.
5. Исследовать на экстремум функцию 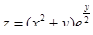 .
.
6. Найти наибольшее и наименьшее значения функции 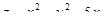 в прямоугольнике, ограниченном прямыми x = 0, x = 6, y = –1, y = 1.
в прямоугольнике, ограниченном прямыми x = 0, x = 6, y = –1, y = 1.
7. Найти градиент функции 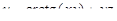 в точке
в точке  .
.
8. Найти производную функции 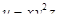 в направлении ее градиента в точке
в направлении ее градиента в точке  .
.
9. Написать уравнение касательной плоскости к эллипсоиду 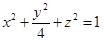 в точке
в точке 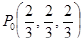 .
.
10. Вычислить двойной интеграл 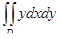 , где D – область, ограниченная линиями y = x,
, где D – область, ограниченная линиями y = x,
y = 0, x = 1.
ТРЕНИНГ КОМПЕТЕНЦИЙ
Дата добавления: 2018-09-23; просмотров: 253; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
