Длина дуги плоской кривой в декартовых координатах
Пусть дуга AB задана уравнением 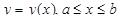 , где функция y(x) – непрерывна и имеет непрерывную производную на отрезке [a, b]. Тогда ее длина s вычисляется по формуле (длины дуги кривой в декартовых координатах)
, где функция y(x) – непрерывна и имеет непрерывную производную на отрезке [a, b]. Тогда ее длина s вычисляется по формуле (длины дуги кривой в декартовых координатах)
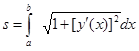 . (3.6)
. (3.6)
Доказательство. Разобьем отрезок [a, b] на n частей точками 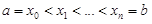 и впишем в дугу AB ломаную
и впишем в дугу AB ломаную 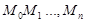 , абсциссами вершин которой были бы точки деления
, абсциссами вершин которой были бы точки деления 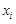
отрезка [a, b] (рис. 15). Пусть 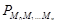 – периметр ломаной,
– периметр ломаной, 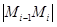 – длина звена
– длина звена 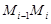 . Тогда
. Тогда 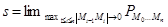 . Положим
. Положим 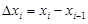 ,
, 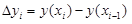 . По теореме Пифагора длина звена
. По теореме Пифагора длина звена 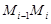 ломаной будет равна
ломаной будет равна 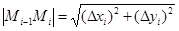 . Так как y(x) – дифференцируемая функция, то по теореме Лагранжа существует точка
. Так как y(x) – дифференцируемая функция, то по теореме Лагранжа существует точка 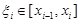 такая, что
такая, что 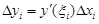 .
.
Тогда 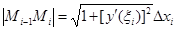 и
и 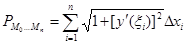 . По условию производная
. По условию производная 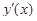 непрерывна. Следовательно, функция
непрерывна. Следовательно, функция 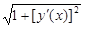 непрерывна. При
непрерывна. При 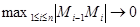 будет также
будет также 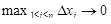 . Поэтому существует конечный предел
. Поэтому существует конечный предел
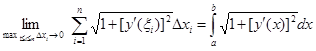 .
.
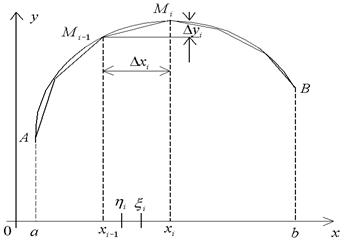
Рис. 15
Тем самым доказана справедливость формулы (3.6).
Пример. Вычислить длину дуги параболы 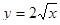 ,
, 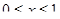 .
.
Решение. Функция 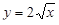 непрерывна на отрезке [0, 1], ее производная
непрерывна на отрезке [0, 1], ее производная 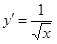 непрерывна на полуинтервале (0, 1] и
непрерывна на полуинтервале (0, 1] и 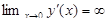 . Поэтому для длины данной дуги параболы по формуле (3.6) получаем несобственный интеграл
. Поэтому для длины данной дуги параболы по формуле (3.6) получаем несобственный интеграл 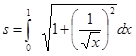 . Определение таких несобственных интегралов было рассмотрено в разделе 2.4.2. По формуле (2.14) вычислим
. Определение таких несобственных интегралов было рассмотрено в разделе 2.4.2. По формуле (2.14) вычислим
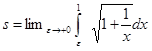 .
.
Имеем
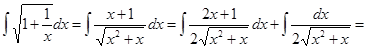
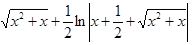 .
.
Тогда
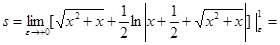
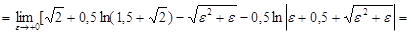
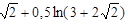 .
.
Длина дуги плоской кривой, заданной параметрическими уравнениями
Пусть дуга AB задана параметрическими уравнениями
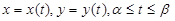 , (*)
, (*)
|
|
|
где x(t), y(t) – непрерывно дифференцируемые функции на отрезке 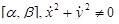 и x(t) – монотонная функция. Тогда длина s дуги AB вычисляется по формуле
и x(t) – монотонная функция. Тогда длина s дуги AB вычисляется по формуле
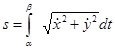 . (3.7)
. (3.7)
Действительно, пусть сначала функция x(t) монотонно возрастает на отрезке 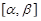 . При сделанных предположениях относительно функций x(t) и y(t) уравнения (*) определяют дифференцируемую функцию y = f(x) и длина дуги может быть вычислена по формуле
. При сделанных предположениях относительно функций x(t) и y(t) уравнения (*) определяют дифференцируемую функцию y = f(x) и длина дуги может быть вычислена по формуле 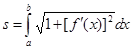 , где
, где 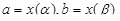 . Сделаем в этом интеграле замену переменной x = x(t). Учитывая, что
. Сделаем в этом интеграле замену переменной x = x(t). Учитывая, что 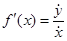 и
и 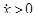 , получим
, получим
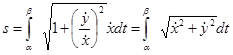 .
.
В случае, когда функция x(t) монотонно убывает на отрезке 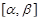 , будет выполняться неравенство a > b и длина дуги будет равна
, будет выполняться неравенство a > b и длина дуги будет равна 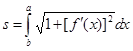 . Делая в интеграле замену переменной x = x(t) и учитывая, что теперь
. Делая в интеграле замену переменной x = x(t) и учитывая, что теперь 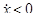 и
и 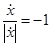 , получим
, получим
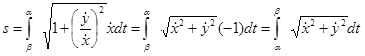 .
.
Пример. Вычислить длину дуги полукубической параболы 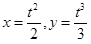 , отсеченной
, отсеченной
прямой x = 1 (рис. 16).
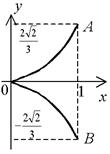
Рис. 16
Решение. Длина s дуги AOB равна удвоенной длине дуги AO. Значение параметра t, соответствующее точке A пересечения параболы с прямой, найдем из системы уравнений 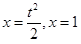 . Получим
. Получим 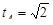 . Аналогично t0 = 0. Тогда
. Аналогично t0 = 0. Тогда
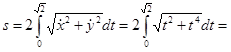
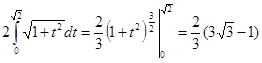 .
.
Замечание. Для длины s дуги пространственной кривой x = x(t), y = y(t), z = z(t), 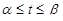 ,
,
где x(t), y(t), z(t) – непрерывно дифференцируемые на отрезке 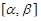 функции, может быть получена формула
функции, может быть получена формула 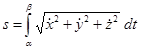 .
.
|
|
|
Длина дуги кривой в полярных координатах
Пусть полюсом и полярной осью полярной системы координат являются начало координат O и ось x декартовой системы координат. Обозначим через 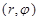 – полярные координаты точки (x, y), так что
– полярные координаты точки (x, y), так что 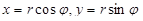 .
.
Пусть дуга AB задана уравнением 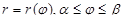 , где
, где 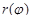 – непрерывно дифференци-руемая функция на отрезке
– непрерывно дифференци-руемая функция на отрезке 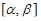 . Тогда длина s дуги AB вычисляется по формуле
. Тогда длина s дуги AB вычисляется по формуле
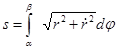 . (3.8)
. (3.8)
Действительно, при 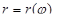 будем иметь параметрические уравнения дуги AB: x = r(j)cosj,
будем иметь параметрические уравнения дуги AB: x = r(j)cosj,
y = r(j)sinj, a £ j £ b.
Тогда по формуле (3.7) длина s дуги AB будет равна интегралу .
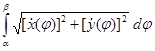 .
.
Найдя 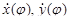 и преобразовывая подкоренное выражение, получим:
и преобразовывая подкоренное выражение, получим:
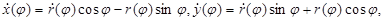
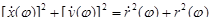 и
и 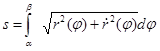 .
.
Пример. Вычислить длину кардиоиды 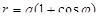 .
.
Решение. Длина s всей кардиоиды равна удвоенной длине ее дуги, вдоль которой j изменяется от 0 до p (рис. 17), так что
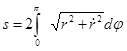 .
.
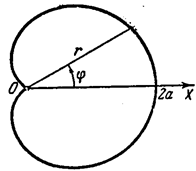
Рис. 17
Имеем:
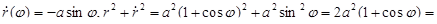
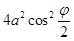
и 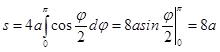 .
.
Дата добавления: 2018-09-23; просмотров: 677; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
