Несобственные интегралы от неограниченных функций на конечном промежутке
Пусть функция f(x) непрерывна на полуинтервале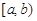 
и неограничена в окрестности точки b. Тогда для любого положительного числа e такого, что 
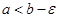, функция f(x) непрерывна на отрезке 
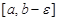и, следовательно, интегрируема на нем. Несобственный интеграл 
определим как предел определенного интеграла 
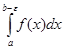при стремлении e к 0 (рис. 4):
. (2.13)
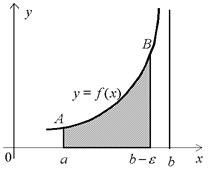
Рис. 4
Если в правой части этого равенства предел интеграла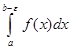 
при 
существует и конечен, то говорят, что несобственный интеграл 
сходится, в противном случае – расходится.
Аналогично для функции f(x), непрерывной на полуинтервале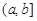 
и неограниченной в окрестности точки a, определим несобственный интеграл 
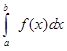от функции f(x) на отрезке [a, b] согласно равенству
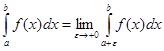, (2.14)
где e – произвольное положительное число такое, что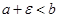 
.
Если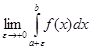 
существует и конечен, то говорят, что несобственный интеграл 
сходится, в противном случае – расходится.
Пусть теперь функция f(x) непрерывна во всех точках отрезка [a, b], кроме внутренней точки c, и неограничена в окрестности этой точки. Тогда несобственный интеграл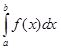 
определим согласно равенству
. (2.15)
Несобственный интеграл 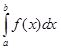сходится, если сходится каждый из двух интегралов в правой части этого равенства, и расходится в противном случае.
Пример. Проверить, что несобственный интеграл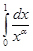 
сходится при 
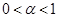и расходится при 
.
|
|
|
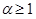Решение. Функция 
непрерывна на полуинтервале (0, 1] и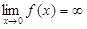 
.
Тогда
.
Пусть 0 < a < 1. Тогда
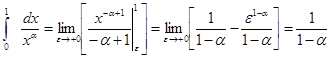, так как 
.
Пусть a > 1. Тогда
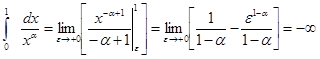, так как 
.
Пусть a = 1. Тогда
.
Следовательно, при 0 < a < 1 данный несобственный интеграл сходится, а при 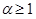расходится.
3. Геометрические и механические приложения
определенного интеграла
В главе 2 мы уже говорили о задачах, решение которых приводит к использованию опреде-ленного интеграла: задачи о вычислении массы неоднородного стержня, работы переменной силы. Рассмотрим ряд геометрических приложений определенного интеграла.
Площадь плоской фигуры
Площадь плоской фигуры в декартовых координатах
Как мы знаем из геометрического смысла определенного интеграла (см. 2.1.3.), площадь S криволинейной трапеции aABb, ограниченной отрезком [a, b] оси x, графиком непрерывной неотрицательной функции f(x) и прямыми x = a, x = b (см. рис. 1), вычисляется по формуле
.
Рассмотрим теперь вычисление площади областей более общего вида.
I. Пусть область D ограничена прямыми x = a, x = b и непрерывными кривыми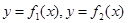 
, где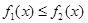 
для любых 
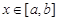(рис. 5, а). Такие области называются правильными относительно оси y. Тогда ее площадь S вычисляется по формуле
|
|
|
. (3.1)
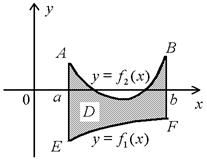
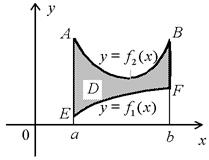
а) б)
Рис. 5
Действительно, в случае 
область D есть разность двух криволинейных трапеций aABb и aEFb (рис. 5,б). Общий же случай сводится к предыдущему с помощью сдвига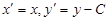 
вдоль оси y вниз, где константа 
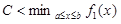(так как при этом разность ординат не меняется).
II. Пусть область D ограничена прямыми y = c, y = d и непрерывными кривыми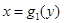 
, 
, где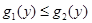 
для любых 
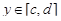(рис. 6). Такие области называются правильными относительно оси x. Тогда ее площадь S вычисляется аналогично по формуле
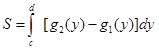. (3.2)
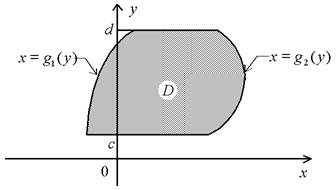
Рис. 6
III. Область D может быть разбита на конечное число областей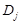 
I-го и II-го типов. Тогда, вычисляя площади каждой из областей 
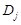, соответственно, по формулам (3.1) и (3.2) и складывая их, получим площадь области D.
Пример 1. Вычислить площадь области, ограниченной кривыми 
и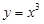 
(рис. 7).
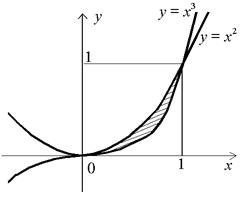
Рис. 7
Решение. Будем рассматривать нашу область как правильную относительно оси y: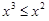 
для любых 
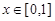. Тогда по формуле (3.1) получим
.
Пример 2. Вычислить площадь области, ограниченной параболой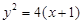 
и прямой 
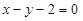(рис. 8).
|
|
|
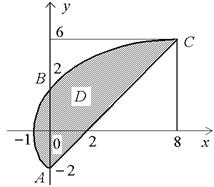
Рис. 8
Решение. Будем рассматривать данную область как правильную относительно оси x. Тогда следует разрешить уравнения параболы и прямой относительно x и найти ординаты точек пересечения параболы с прямой. Имеем:
,
.
Решая систему этих уравнений, получим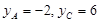 
. Тогда 
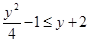для любых 
и по формуле (3.2) вычислим
.
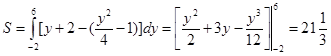Дата добавления: 2018-09-23; просмотров: 256; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!