Определение определенного интеграла Римана
Пусть на отрезке [a, b] оси x определена функция f(x). Разобьем отрезок [a, b] произвольным образом на n частей точками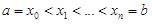 
. На каждом отрезке 
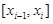длины 
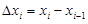выберем произвольную точку 
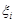. Составим сумму 
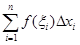, называемую интегральной суммой Римана для функции f( x) на отрезке [ a, b]. Определенным интегралом Римана от функции f( x) на отрезке [ a, b] называется число, обозначаемое символом 
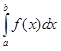и равное пределу интегральных сумм при стремлении к нулю максимальной из длин отрезков разбиения
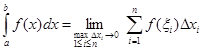, (2.1)
если этот предел существует, конечен и не зависит от способа разбиения отрезка [a, b] на части и выбора точек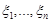 
на отрезках 
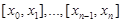. Число a называется нижним пределом интегрирования, число b – верхним пределом интегрирования. Функция f(x), для которой существует определенный интеграл 
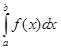, называется интегрируемой на отрезке [a, b]. Под пределом интегральных сумм в правой части равенства (2.1) понимается число J, удовлетво-ряющее условию: для любого (сколь угодно малого) положительного числа e найдется такое поло-жительное число d, что при 
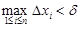и любом выборе точек 
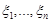выполняется неравенство
.
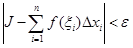Дополнение к определению определенного интеграла
Выше, вводя определенный интеграл, мы полагали a < b. Положим по определению:
1) 
,
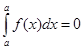2) 
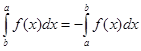
для любых a и b (при перестановке пределов интегрирования определенный интеграл меняет знак).
Пусть функция f(x) непрерывна на отрезке [a, b]. Положим на каждом отрезке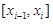 
|
|
|
,
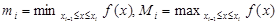и пусть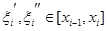 
– точки, в которых 
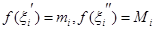, так что для любого 
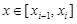выполняются неравенства 
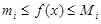. Суммы 
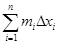и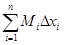 
называются, соответственно, нижними и верхними интегральными суммами. Очевидно, при одном и том же разбиении
отрезка [a, b] всякая интегральная сумма не меньше нижней и не больше верхней интегральных сумм:
.
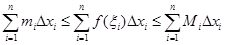Отсюда следует, что для существования определенного интеграла необходимо и достаточно, чтобы существовал общий конечный предел нижних и верхних интегральных сумм при стремлении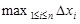 
к 0. Можно доказать, что если функция f(x) непрерывна на отрезке [a, b], то определенный интеграл 
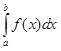существует. Другими словами: всякая непрерывная на отрезке функция интегрируема на этом отрезке. Интегрируемыми являются также кусочно непрерывные функции, то есть функции, имеющие на отрезке лишь конечное число точек разрыва 1-го рода. Можно также доказать, что всякая интегрируемая на отрезке функция ограничена на этом отрезке.
2.1.3. Геометрический смысл верхних и нижних интегральных сумм
и определенного интеграла от неотрицательной функции
Пусть на отрезке [a, b] функция f(x) неотрицательна. Назовем криволинейной трапецией фигуру, ограниченную отрезком [a, b] оси x, дугой AB графика функции f(x) и прямыми x = a и x = b (рис. 1).
|
|
|
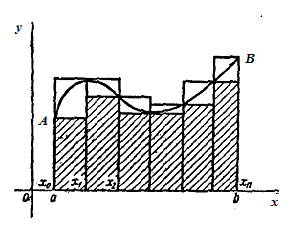
Рис. 1
Каждый член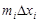 
нижней интегральной суммы равен площади прямоугольника высоты 
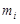, имеющего основанием отрезок 
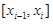, а вся нижняя интегральная сумма равна площади, составленной из таких прямоугольников ступенчатой фигуры, вписанной в криволинейную трапецию (на рисунке эта ступенчатая фигура заштрихована). Аналогично верхняя интегральная сумма равна площади описанной около криволинейной трапеции ступенчатой фигуры. Тогда определенный интеграл, являющийся общим пределом нижних и верхних интегральных сумм, равен общему пределу площадей, вписанных в криволинейную трапецию и описанных около нее ступенчатых фигур, который и принимается за площадь криволинейной трапеции. Таким образом, мы приходим к следующему геометрическому смыслу определенного интеграла: определенный интеграл 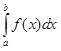от неотрицательной на отрезке [a, b] функции f(x) равен площади криволинейной трапеции aABb.
Дата добавления: 2018-09-23; просмотров: 202; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!