Понятие неопределенного интеграла
Современная
Гуманитарная
Академия
Дистанционное образование
РУ.01.2
Рабочий учебник
Фамилия, имя, отчество обучающегося __________________________________________________
Направление подготовки ______________________________________________________________
Номер контракта _____________________________________________________________________
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Юнита 3
Интегральное исчисление функций одной переменной
МОСКВА 2009
Разработано Е.А. Кошелевой, канд. техн. наук, доц.
Под ред. Б.П. Осиленкера, д-ра физ.-мат. наук, проф.
Рекомендовано Учебно-методическим советом в качестве учебного пособия для студентов СГА
КУРС: МАТЕМАТИЧЕСКИЙ АНаЛИЗ
Юнита 1. Элементы математической логики. Теория множеств. Функции.
Юнита 2. Дифференциальное исчисление функций одной переменной.
Юнита 3. Интегральное исчисление функций одной переменной.
Юнита 4. Дифференциальное и интегральное исчисление функций нескольких переменных.
Юнита 5. Дифференциальные уравнения.
Юнита 6. Ряды. Ряды Фурье.
ЮНИТА 3
Рассмотрены вопросы интегрирования функций одной переменной. Определяется первообразная функции, вводится понятие определенного интеграла от функции, заданной на отрезке. Приводятся геометрические, механические и физические приложения интегралов.
Рабочий учебник составлен на основе дидактических единиц учебников, имеющих гриф Министерства образования и науки Российской Федерации или Учебно-методического объединения:
|
|
|
1. Ильин, В. А. Высшая математика [ЭР] : учебник для ВУЗов / В. А. Ильин, А. В. Куркина. - М. : Проспект, 2008.
2. Кудрявцев, Л. Д. Краткий курс математического анализа [ЭР] / Л. Д. Кудрявцев. - М. : Физматлит, 2005. Т. 2.
3. Кудрявцев, Л. Д. Математический анализ [Текст] : в 3 т / Л. Д. Кудрявцев. - М. : Дрофа, Т. 1, 2004. Т. 2, 2004, Т. 3, 2006.
Для студентов Современной Гуманитарной Академии
_____________________________________________________________________________________
© СОВРЕМЕННАЯ ГУМАНИТАРНАЯ АКАДЕМИЯ, 2009
(настоящее учебное пособие не может быть полностью или частично воспроизведено, тиражировано
и распространено в качестве официального издания без разрешения руководства СГА)
Соответствие системы менеджмента качества СГА в сфере создания информационных образовательных ресурсов требованиям международного стандарта ISO 9001:2000 (ГОСТ Р ИСО 9001-2001)
подтверждено Сертификатом соответствия Стандарт-тест
ОГЛАВЛЕНИЕ
Стр.
Дидактический план.. 4
ЛИТЕРАТУРА.. 5
ПЕРЕЧЕНЬ УМЕНИЙ.. 7
Тематический обзор. 10
1. Неопределенный интеграл.. 10
1.1. Определение неопределенного интеграла, его свойства; таблица интегралов от основных элементарных функций. 10
|
|
|
1.1.1. Понятие неопределенного интеграла. 10
1.1.2. Основные свойства неопределенного интеграла. 11
1.1.3. Таблица основных интегралов. 11
1.2. Замена переменной и интегрирование по частям в неопределенном интеграле. 12
1.2.1. Замена переменной. 12
1.2.2. Интегрирование по частям.. 14
1.3. Интегрирование рациональных функций. 14
1.4. Методы интегрирования некоторых тригонометрических и иррациональных выражений. 18
2. Определенный интеграл.. 21
2.1. Определение определенного интеграла, условия его существования. Свойства определенного интеграла. 21
2.1.1. Задачи, приводящие к понятию определенного интеграла. 21
2.1.2. Определение определенного интеграла Римана. 23
2.1.3. Геометрический смысл верхних и нижних интегральных сумм и определенного интеграла от неотрицательной функции. 24
2.1.4. Основные свойства определенного интеграла. 25
2.2. Интеграл с переменным верхним пределом, его непрерывность и дифференцируемость. Формула Ньютона–Лейбница. 27
2.2.1. Интеграл с переменным верхним пределом.. 27
2.2.2. Формула Ньютона–Лейбница. 28
2.3. Замена переменной и интегрирование по частям в определенном интеграле. 29
2.3.1. Замена переменной в определенном интеграле. 29
2.3.2. Интегрирование по частям в определенном интеграле. 29
|
|
|
2.4. Несобственные интегралы.. 30
2.4.1. Несобственные интегралы от непрерывных функций на бесконечном промежутке. 30
2.4.2. Несобственные интегралы от неограниченных функций на конечном промежутке. 32
3. Геометрические и механические приложения определенного интеграла 33
3.1. Площадь плоской фигуры.. 33
3.1.1. Площадь плоской фигуры в декартовых координатах. 33
3.1.2. Площадь плоской фигуры в полярных координатах. 36
3.1.3. Площадь плоской фигуры в случае параметрического задания граничной кривой. 37
3.2. Объем тела вращения. 38
3.2.1. Формула для вычисления объема тела через площади его параллельных сечений. 38
3.2.2. Формула для вычисления объема тела вращения. 38
3.3. Длина дуги кривой. 39
3.3.1. Длина дуги плоской кривой в декартовых координатах. 39
3.3.2. Длина дуги плоской кривой, заданной параметрическими уравнениями. 41
3.3.3. Длина дуги кривой в полярных координатах. 42
3.3.4. Дифференциал переменной длины дуги. 43
3.4. Площадь поверхности вращения. 44
Задания для самостоятельной работы... 46
ТРЕНИНГ УМЕНИЙ.. 52
ГЛОССАРИЙ.. 66
Дидактический план
Неопределенный интеграл, его свойства. Методы интегрирования: замена переменной и интегрирование по частям, интегрирование рациональных функций и рационализирующие подстановки для некоторых классов интегралов от тригонометрических и иррациональных выражений.
|
|
|
Определенный интеграл как предел интегральных сумм, его свойства и связь с неопреде-ленным интегралом. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.
Несобственные интегралы.
Геометрические и механические приложения определенного интеграла: площадь плоской фигуры, объем тела вращения, длина дуги, площадь поверхности вращения, масса и центр тяжести неоднородного стержня.
ЛИТЕРАТУРА *
1. Бугров, Я. С. Высшая математика [Текст] : в 3 т / Я. С. Бугров, С. М. Никольский. – М. : Дрофа, Т. 1, 2006. Т. 2, 2007. Т. 3, 2005. (Гриф МО РФ).
2. Данилов Ю. М., Журбенко Л. Н., Никонова Г. А., Никонова Н. В., Нуриева С. Н. Математика. Гриф МО РФ [Текст]: Учеб. пособие - ("Высшее образование") / Данилов Ю.М., Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-002673-2.
3. Ермаков В.И. Справочник по математике для экономистов. Гриф МО РФ [Текст]: Учебное пособие - 3-е изд., перераб. и доп. - ("Высшее образование") / Ермаков В.И. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-003542-0.
4. Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Дегтярева О.М. Математика в примерах и задачах. Гриф МО РФ [Текст]: Учеб. пособие - ("Высшее образование") / Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Дегтярева О.М. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-003449-2.
5. Ильин, В. А. Высшая математика [ЭР] : учебник для ВУЗов / В. А. Ильин, А. В. Куркина. - М. : Проспект, 2008. (с грифом УМО).
6. Клюшин В. Л. Высшая математика для экономистов. Гриф МО РФ [Текст]: Учеб. пособие - ("Учебники РУДН") / Клюшин В.Л. - М.: ИНФРА-М,-2009. - ISBN: 978-5-16-002752-4.
7. Кудрявцев, Л. Д. Краткий курс математического анализа [ЭР] / Л. Д. Кудрявцев. - М. : Физматлит, 2005. Т. 2. (с грифом УМО) Электронная библиотека "Мир книг" (www.mirknig.su).
8. Кудрявцев, Л. Д. Математический анализ [Текст] : в 3 т / Л. Д. Кудрявцев. - М. : Дрофа,
Т. 1, 2004. Т. 2, 2004, Т. 3, 2006. (с грифом МО РФ).
9. Кузнецов, Б. Т. Математика [Текст] : учебник для студентов вузов, обучающихся по специальностям экономики и управления / Б. Т. Кузнецов. - 2-е изд., перераб. и доп. - М. : ЮНИТИ-ДАНА, 2004. - 719 с. - ISBN 5-238-00754-Х.
10. Малыхин В. И. Высшая математика. Гриф МО РФ [Текст]: Учебное пособие - 2-е изд., перераб. и доп. - ("Высшее образование") / Малыхин В.И. - М.: ИНФРА-М,-2009. - ISBN: 5-16-002625-8.
11. Пискунов, Н. С. Дифференциальные и интегральные исчисления [Текст] : в 2 т /
Н. С. Пискунов. – М. : Интеграл-Пресс, 2007. (Гриф МО РФ).
12. Фихтенгольц, Г. М. Курс дифференциального и интегрального исчисления [Текст] : в 3 т / Г. М. Фихтенгольц. - М. : Физматлит, Т. 1, 2007. Т. 2 , 206. Т. 3, 2008. (Гриф МО РФ).
ПЕРЕЧЕНЬ УМЕНИЙ
| № п/п | Умение | Алгоритм |
| 1 | Найти интеграл 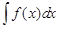 , использовав таблицу основ-ных интегралов и основные свойства неопределенного ин-теграла:
1) , использовав таблицу основ-ных интегралов и основные свойства неопределенного ин-теграла:
1) 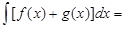
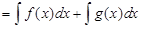 ;
2) ;
2) 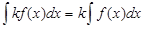 k = const, k ¹ 0
k = const, k ¹ 0
| 1. Использовать свойства неопределенного интеграла. 2. Использовать таблицу основных интегралов и вычис-лить имеющиеся неопределенные интегралы. 3. Записать ответ |
| 2 | Найти интеграл 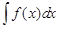 мето-дом замены переменной мето-дом замены переменной
| 1. Подобрать замену переменной:
 или или 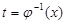 .
2. Выразить подынтегральную функцию через новую переменную .
2. Выразить подынтегральную функцию через новую переменную
 .
3. Выразить dx через t и dt, используя равенства .
3. Выразить dx через t и dt, используя равенства
 или
или 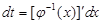 .
4. Записать данный интеграл по формуле замены пере-менной .
4. Записать данный интеграл по формуле замены пере-менной
 .
5. Применить к полученному интегралу основные свойства неопределенного интеграла и воспользоваться таблицей основных интегралов.
6. Вернуться от переменной t к исходной переменной x, подставив .
5. Применить к полученному интегралу основные свойства неопределенного интеграла и воспользоваться таблицей основных интегралов.
6. Вернуться от переменной t к исходной переменной x, подставив 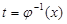
|
| 3 | Найти интеграл 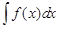 мето-дом интегрирования по частям мето-дом интегрирования по частям
| 1. Представить подынтегральное выражение  в виде произведения в виде произведения 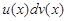 .
2. Найти .
2. Найти  и и 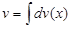 .
3. Применить формулу интегрирования по частям: .
3. Применить формулу интегрирования по частям:
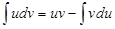 .
4. Найти интеграл .
4. Найти интеграл  .
5. Подставить результат в найденное в пункте (3) выражение .
5. Подставить результат в найденное в пункте (3) выражение
|
| 4 | Вычислить интеграл от дробно-рациональной функции | 1. Убедиться, что данная функция является правильной дробью. В противном случае выделить целую часть. 2. Представить дробь в виде суммы многочлена и правильной рациональной дроби. 3. Разложить знаменатель дроби на произведение линей-ных и квадратичных множителей, используя раздел 1.3 юниты. 4. Разложить правильную дробь на сумму простейших дробей. 5. Используя свойства интеграла и табличные формулы, найти интегралы от каждого слагаемого |
| № п/п | Умение | Алгоритм |
| 5 | Вычисление определенного интеграла 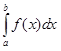 по формуле Ньютона–Лейбница по формуле Ньютона–Лейбница
| 1. Найти одну из первообразных F(x) функции f(x).
2. Вычислить значение первообразной F(x) в точках x = a и x = b.
3. Вычислить значение определенного интеграла по формуле
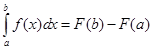
|
| 6 | Вычисление определенного интеграла 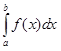 методом замены переменной методом замены переменной
| 1. Выбрать замену переменной  ( (  – моно-тонная непрерывно дифференцируемая функция).
2. Перейти в подынтегральном выражении от переменной x к новой переменной t: – моно-тонная непрерывно дифференцируемая функция).
2. Перейти в подынтегральном выражении от переменной x к новой переменной t:
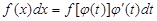 .
3. Найти пределы интегрирования по новой переменной t из равенств: .
3. Найти пределы интегрирования по новой переменной t из равенств:
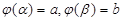 .
4. Записать данный интеграл по формуле замены пере-менной .
4. Записать данный интеграл по формуле замены пере-менной
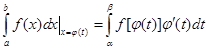 .
5. Вычислить определенный интеграл в правой части последнего равенства по формуле Ньютона–Лейбница .
5. Вычислить определенный интеграл в правой части последнего равенства по формуле Ньютона–Лейбница
|
| 7 | Применение определенного интеграла к вычислению: а) площадей плоских фигур; б) объемов тел вращения | а. Вычисление площадей плоских фигур
1. Построить данные кривые и ограниченную ими область.
2. Определить, является ли данная область правильной относительно оси Oy –
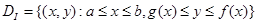 или правильной относительно оси Ox –
или правильной относительно оси Ox –
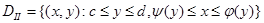 ,
и если такой не является, то разбить ее на конечное число областей указанного вида.
3. Вычислить площадь каждой из областей типа ,
и если такой не является, то разбить ее на конечное число областей указанного вида.
3. Вычислить площадь каждой из областей типа 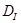 по формуле по формуле
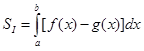 ,
а площадь каждой из областей типа ,
а площадь каждой из областей типа 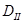 по формуле по формуле
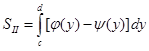 .
4. Сложить полученные значения площадей всех областей.
б. Вычисление объемов тел вращения
1. Построить кривые и область, ими ограниченную.
2. Если данная область – криволинейная трапеция .
4. Сложить полученные значения площадей всех областей.
б. Вычисление объемов тел вращения
1. Построить кривые и область, ими ограниченную.
2. Если данная область – криволинейная трапеция
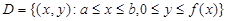 ,
то объем тела, образованного вращением области D вокруг оси Ox, вычислить по формуле ,
то объем тела, образованного вращением области D вокруг оси Ox, вычислить по формуле

|
| № п/п | Умение | Алгоритм |
В случае, когда данная область – область типа
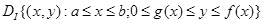 ,
объем тела, образованного вращением области ,
объем тела, образованного вращением области 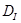 вокруг оси Ox, вычислить по формуле вокруг оси Ox, вычислить по формуле

|
Тематический обзор *
Неопределенный интеграл
1.1. Определение неопределенного интеграла, его свойства;
таблица интегралов от основных элементарных функций
В этой главе будет рассматриваться задача, обратная задаче нахождения производной функции, а именно, задача восстановления функции по ее производной.
Понятие неопределенного интеграла
Функция F(x) называется первообразной функции f( x) на промежутке ( a; b), если она дифференцируема на этом интервале и в каждой его точке 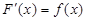 .
.
Например, первообразными функции  являются функции
являются функции  и
и 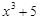 , так как
, так как 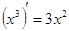 и
и  .
.
Заметим, что вообще, если F(x) первообразная f(x), то F(x) + C, где C – произвольная постоянная, также является первообразной f(x), так как 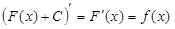 . Таким образом, по производной функция восстанавливается неоднозначно.
. Таким образом, по производной функция восстанавливается неоднозначно.
Убедимся, что всякая первообразная функции f(x) содержится в множестве функций F(x) + C при некотором значении C. Действительно, пусть 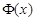 – какая-нибудь отличная от F(x) первообразная функции f(x). Положим
– какая-нибудь отличная от F(x) первообразная функции f(x). Положим  . Тогда
. Тогда
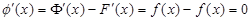 .
.
Согласно известному из дифференциального исчисления условию постоянства функции получаем, что 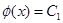 или
или  , где C1 – константа, равная, например,
, где C1 – константа, равная, например, 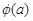 . Следовательно,
. Следовательно, 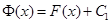 и
и 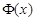 принадлежит совокупности первообразных F(x) + C
принадлежит совокупности первообразных F(x) + C
при C = C1.
Определение. Совокупность всех первообразных функции f(x) называется неопределенным интегралом от функции f(x). Он обозначается символом 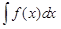 . При этом функцию f(x) называют подынтегральной функцией, выражение
. При этом функцию f(x) называют подынтегральной функцией, выражение  – подынтегральным выражением, знак
– подынтегральным выражением, знак 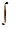 – знаком интеграла.
– знаком интеграла.
Из определения и изложенного выше следует, что если F(x) – какая-нибудь первообразная функции f(x), то
 , (1.1)
, (1.1)
где C – произвольная постоянная. Нахождение неопределенного интеграла 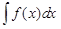 называется интегрированием функции f(x).
называется интегрированием функции f(x).
Отметим, что всякая непрерывная функция имеет в области непрерывности первообразную.
Дата добавления: 2018-09-23; просмотров: 188; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
