Замена переменной и интегрирование по частям в определенном интеграле
Замена переменной в определенном интеграле
Пусть функция f(x) непрерывна на некотором интервале, функция 
монотонна, непре-рывно дифференцируема на отрезке [a, b] и ее значения принадлежат интервалу непрерывности функции f(x). (Тем самым на отрезке [a, b] определена и непрерывна сложная функция 
.) Пусть 
.
Тогда справедливо равенство (формула замены переменной в определенном интеграле)
. (2.8)
Доказательство. Обозначим через F(x) первообразную функции f(x) (она существует, так как функция f(x) непрерывна). Функция 
по условию монотонна, непрерывно дифференцируема и ее значения принадлежат интервалу непрерывности функции f(x). Тогда справедлива формула (1.2) замены переменой в неопределенном интеграле и функция 
является первообразной функции 
. По формуле Ньютона–Лейбница имеем:
,
.
Но так как 
, 
, то правые части этих равенств равны. Тогда равны и левые части и формула (2.8) верна.
Замечание. Если при замене переменной в неопределенном интеграле мы от новой переменной t возвращались к первоначальной переменной x, то при замене переменной в определенном интеграле в этом нет необходимости.
Пример. Вычислить интеграл 
.
Решение. Положим 
. Имеем: x = 0 при t = 0, x = 2 при 
. На отрезке 
функция 2sint монотонна, непрерывно дифференцируема и ее значения не выходят за пределы отрезка [0,2], на котором подынтегральная функция 
непрерывна. Следовательно, можно воспользоваться заменой переменной . Тогда 
и
|
|
|
.
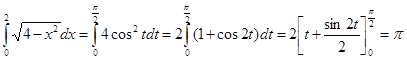Интегрирование по частям в определенном интеграле
Пусть функции u(x) и v(x) непрерывно дифференцируемы на отрезке [a, b]. Тогда справедливо равенство
. (*)
Доказательство. Продифференцируем произведение функций u(x) и v(x):
.
Проинтегрируем это равенство на отрезке [a, b]:
.
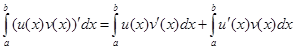Применяя к интегралу в левой части этого равенства формулу Ньютона–Лейбница, получим
.
Отсюда следует доказываемое утверждение. Равенство (*) с учетом того, что 
, записывают короче в виде
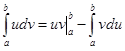(2.9)
и называют формулой интегрирования по частям в определенном интеграле.
Пример. Вычислить интеграл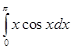 
.
Решение. Положим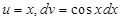 
. Найдем отсюда 
, 
. Тогда
.
Несобственные интегралы
Несобственные интегралы являются обобщением понятия определенного интеграла на случаи: 1) когда областью интегрирования является не отрезок [a, b], а полупрямые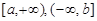 
или вся прямая 
; 2) когда функция имеет точки разрыва 2-го рода, в окрестностях которых функция неограничена.
Несобственные интегралы от непрерывных функций на бесконечном промежутке
|
|
|
Пусть функция f(x) непрерывна на полупрямой 
. Тогда для любого числа b, b > a, функция f(x) непрерывна на отрезке [a, b] и определенный интеграл 
существует. Будем рассматривать его как функцию верхнего предела b и перейдем к пределу при 
. Положим
. (2.10)
Стоящий в левой части этого равенства интеграл называется несобственным интегралом от функции f(x) на промежутке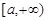 
. На рис. 3 в случае неотрицательной функции f(x) проиллюстрировано вычисление площади фигуры, ограниченной снизу полупрямой 
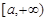, сверху графиком функции f(x) и слева прямой x = a, как предела площади криволинейной трапеции aABb при 
.
Рис. 3
Если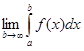 
существует и конечен, то говорят, что несобственный интеграл 
сходится. В противном случае (когда предел бесконечен или не существует) говорят, что несобственный интеграл расходится.
Аналогично вводится несобственный интеграл от функции f(x), непрерывной на полупрямой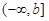 
:
(2.11)
и говорят, что он сходится, если этот предел существует и конечен, и расходится – в противном случае.
Несобственный интеграл от непрерывной функции на всей прямой 
определяется равенством
|
|
|
, (2.12)
где c – произвольно фиксированная точка. При этом говорят, что он сходится, если сходится каждый из двух несобственных интегралов в правой части этого равенства, и расходится, если хотя бы один из несобственных интегралов справа расходится.
Пример 1. 
, данный несобственный интеграл сходится.
Пример 2. 
, но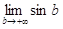 
не существует. Следовательно, данный несобственный интеграл расходится.
Пример 3.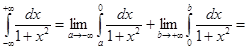 
.
Таким образом, данный несобственный интеграл сходится и равен p.
Дата добавления: 2018-09-23; просмотров: 723; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!