Интегрирование рациональных функций
1. Рациональными функциями называются многочлены P(x) и рациональные дроби  , представляющие собой отношение двух многочленов P(x) и Q(x). Приведем необходимые для дальнейшего сведения из алгебры о рациональных функциях. Доказательства приведенных ниже утверждений можно найти в [5].
, представляющие собой отношение двух многочленов P(x) и Q(x). Приведем необходимые для дальнейшего сведения из алгебры о рациональных функциях. Доказательства приведенных ниже утверждений можно найти в [5].
Пусть 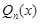 – многочлен степени n, где
– многочлен степени n, где  . Число a называется корнем или нулем многочлена
. Число a называется корнем или нулем многочлена 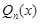 , если
, если 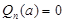 .
.
Теорема Безу. Многочлен 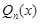 делится на x – a без остатка тогда и только тогда, когда число a является корнем многочлена
делится на x – a без остатка тогда и только тогда, когда число a является корнем многочлена 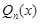 .
.
Таким образом, 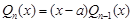 . Корень a называется k-кратным, если
. Корень a называется k-кратным, если 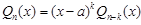 , где
, где  . При k = 1 корень называется простым.
. При k = 1 корень называется простым.
Будем рассматривать многочлены с действительными коэффициентами. Квадратный трехчлен 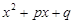 , где p, q – действительные числа, при
, где p, q – действительные числа, при 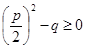 имеет действительные корни x1, x2 и, следовательно, разлагается на линейные множители с действительными коэффициентами
имеет действительные корни x1, x2 и, следовательно, разлагается на линейные множители с действительными коэффициентами 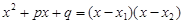 , а при
, а при 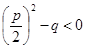 имеет комплексно сопряженные корни
имеет комплексно сопряженные корни  ,
,  , где
, где 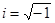 , и на линейные множители с действительными коэффициентами не разлагается. В курсе алгебры доказывается, что всякий отличный от константы многочлен с действительными коэффициентами произвольной степени разлагается на линейные или квадратичные множители с действительными коэффициентами.
, и на линейные множители с действительными коэффициентами не разлагается. В курсе алгебры доказывается, что всякий отличный от константы многочлен с действительными коэффициентами произвольной степени разлагается на линейные или квадратичные множители с действительными коэффициентами.
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. В противном случае называется неправильной. Всякую неправильную рациональную дробь можно, деля числитель на знаменатель, представить в виде суммы многочлена, называемого целой частью дроби, и правильной рациональной дроби.
|
|
|
Например: 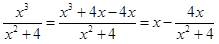 .
.
Будем теперь рассматривать правильные рациональные дроби с действительными коэффи-циентами многочленов в числителе и знаменателе. Среди них назовем простейшими дроби вида:
1. 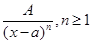 ,
,
2. 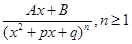 ,
,
где 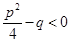 .
.
Теорема. Пусть 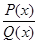 – правильная рациональная дробь, у которой P(x) и Q(x) – многочлены с действительными коэффициентами и разложение знаменателя Q(x) на линейные и квадратичные множители имеет вид
– правильная рациональная дробь, у которой P(x) и Q(x) – многочлены с действительными коэффициентами и разложение знаменателя Q(x) на линейные и квадратичные множители имеет вид
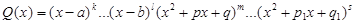 ,
,
где 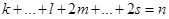 , n – степень многочлена Q(x),
, n – степень многочлена Q(x),  .
.
Тогда дробь 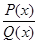 представима в виде суммы простейших дробей поправилу:
представима в виде суммы простейших дробей поправилу:
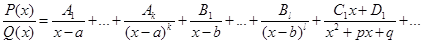
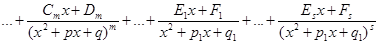 , (1.4)
, (1.4)
где 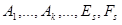 – действительные числа, называемые неопределенными коэффициентами.
– действительные числа, называемые неопределенными коэффициентами.
Тождество (1.4) называется разложением дроби на простейшие. Неопределенные коэффи-циенты находятся однозначно.
Практическое правило нахождения неопределенных коэффициентов:
1. Умножаем равенство (1.4) на общий знаменатель всех дробей. Получим тождественное равенство двух многочленов.
2. Далее возможны два варианта.
Первый вариант основывается на том, что два многочлена тождественно равны тогда и только тогда, когда их коэффициенты при одинаковых степенях равны. Поэтому, раскрывая скобки и приводя в правой части подобные члены, приравниваем коэффициенты при одинаковых степенях x в правой и левой частях равенства. Получаем систему линейных алгебраических уравнений относительно неопределенных коэффициентов.
|
|
|
Пример. Разложить дробь 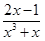 на простейшие.
на простейшие.
Решение. Разложим знаменатель на линейные и квадратичные множители с действительными коэффициентами 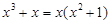 и запишем разложение данной дроби на простейшие с неопределенными коэффициентами:
и запишем разложение данной дроби на простейшие с неопределенными коэффициентами:
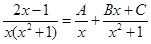 .
.
Умножая это равенство на общий знаменатель 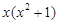 , получим
, получим
 .
.
Приравниваем коэффициенты при одинаковых степенях x в правой и левой частях этого равенства.
При 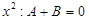 .
.
При 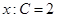 .
.
При  .
.
Тогда 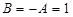 и
и 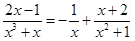 .
.
Второй вариант составления системы относительно неопределенных коэффициентов: не раскрывая скобок, даем аргументу x столько различных значений, сколько имеется неопреде-ленных коэффициентов, используя в первую очередь корни знаменателя. (Нужно при этом следить за тем, чтобы уравнения в системе были независимыми.)
Пример. Разложить дробь 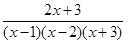 на простейшие.
на простейшие.
Решение. Представим дробь в виде суммы простейших с неопределенными коэффициентами
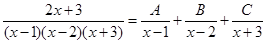 .
.
Умножая это равенство на общий знаменатель, получим
|
|
|
 .
.
Будем давать x последовательно значения 1, 2, –3. Получим систему
5 = –4A, 7 = 5B, –3 = 20C,
откуда 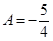 ,
, 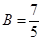 ,
, 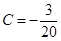 и
и
 .
.
2. Перейдем к методам интегрирования простейших дробей. Для интеграла от дроби 1-го типа имеем:
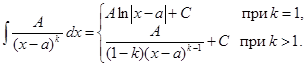
Рассмотрим интеграл от дроби 2-го типа при k = 1:
 ,
,
где 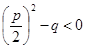 .
.
Выделим в числителе производную квадратного трехчлена 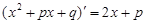 и преобра-зуем интеграл в сумму двух интегралов:
и преобра-зуем интеграл в сумму двух интегралов:
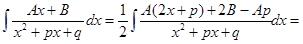
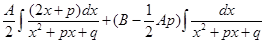 .
.
Замена переменной 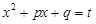 в первом интеграле приводит его к табличному интегралу (III). Второй интеграл после выделения из квадратного трехчлена полного квадрата суммы
в первом интеграле приводит его к табличному интегралу (III). Второй интеграл после выделения из квадратного трехчлена полного квадрата суммы 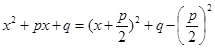 и замены переменной
и замены переменной 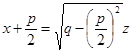 преобразуется в табличный интеграл (X). В итоге получим
преобразуется в табличный интеграл (X). В итоге получим
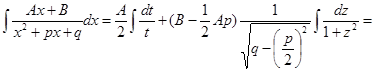
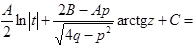
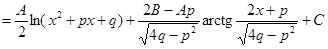 .
.
Интеграл  , где
, где 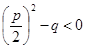 и k > 1, после выделения в числителе произ-водной квадратного трехчлена
и k > 1, после выделения в числителе произ-водной квадратного трехчлена 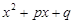 представляют, как и выше, в виде суммы двух интегралов, один из которых заменой
представляют, как и выше, в виде суммы двух интегралов, один из которых заменой 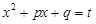 сводится к табличному интегралу (II), а второй интегрированием по частям сводится к рассмотренным выше интегралам.
сводится к табличному интегралу (II), а второй интегрированием по частям сводится к рассмотренным выше интегралам.
Итак, интегралы от простейших рациональных дробей выражаются через элементарные функции. А так как всякая рациональная дробь представима в виде суммы многочлена и простейших дробей, то интегралы от всякой рациональной функции выражаются через элемен-тарные функции.
Пример. Найти  .
.
|
|
|
Решение. Выделяем целую часть дроби
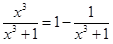 .
.
Разлагаем знаменатель дроби на множители с действительными коэффициентами  . Разлагаем дробь
. Разлагаем дробь 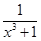 на простейшие:
на простейшие:
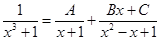 .
.
Умножая это равенство на общий знаменатель, получаем
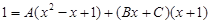 .
.
Приравниваем коэффициенты при одинаковых степенях x справа и слева.
При x2:.. A + B = 0.
При x:.. –A + B + C = 0.
При x0:.. A + C = 1.
Отсюда 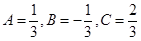 и
и 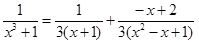 .
.
Тогда

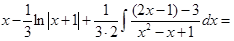
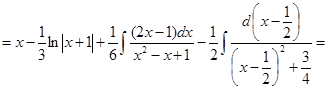
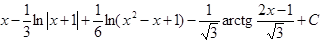 .
.
Дата добавления: 2018-09-23; просмотров: 196; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
