Основные свойства неопределенного интеграла
1. Так как операция интегрирования есть операция, обратная дифференцированию, то справедливы равенства:
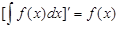 ;
; 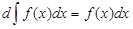 ;
;
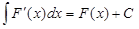 ;
; 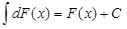 .
.
Справедливость следующих равенств легко установить дифференцированием их левых и правых частей.
2. 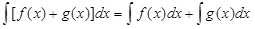 .
.
3. 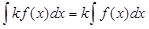 ,
,
где k – постоянный множитель, отличный от нуля.
Всякая формула дифференцирования, прочитанная справа налево, порождает формулу интегрирования.
Таблица основных интегралов
Каждое из приведенных ниже равенств рассматривается в области, где подынтегральная функция и ее первообразная непрерывны. В правых частях этих равенств C – произвольная постоянная.
Из таблиц производных следуют формулы:
I.  .
.
II.  ,
,  .
.
III.  .
.
IV. 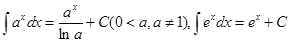 .
.
V.  .
.
VI. 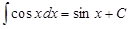 .
.
VII. 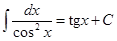 .
.
VIII.  .
.
IX. 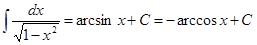 .
.
X.  .
.
Следующие две формулы нетрудно проверить дифференцированием.
XI. 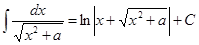 .
.
XII. 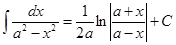 ,
, 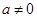 .
.
Рассмотренные свойства и таблица интегралов позволяют уже находить интегралы от простейших функций.
Пример. Найти  .
.
Решение. Воспользуемся свойствами 2 и 3 и табличным интегралом (II). Получим
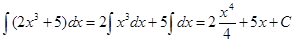 .
.
Заметим, что результат дифференцирования элементарных функций является снова элемен-тарной функцией, тогда как операция интегрирования элементарных функций может привести к новым функциям, которые не могут быть представлены в виде суперпозиций элементарных функций. Например, доказано, что следующие интегралы существуют, но не выражаются через элементарные функции:
 – интеграл Пуассона,
– интеграл Пуассона,
|
|
|
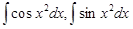 – интегралы Френеля,
– интегралы Френеля,
 – интегральный логарифм,
– интегральный логарифм,
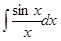 – интегральный синус,
– интегральный синус,
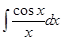 – интегральный косинус.
– интегральный косинус.
Перейдем к рассмотрению основных методов интегрирования.
Замена переменной и интегрирование по частям в неопределенном интеграле
Замена переменной
Пусть функция  монотонна и имеет непрерывную производную на некотором проме-жутке изменения переменной t, функция f(x) непрерывна на интервале, принадлежащем области значений функции
монотонна и имеет непрерывную производную на некотором проме-жутке изменения переменной t, функция f(x) непрерывна на интервале, принадлежащем области значений функции  , так что определена сложная функция
, так что определена сложная функция 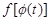 . Тогда справедливо равенство
. Тогда справедливо равенство
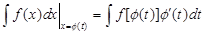 , (1.2)
, (1.2)
называемое формулой замены переменной в неопределенном интеграле.
Действительно, дифференцируя левую часть этого равенства по t по правилу дифферен-цирования сложной функции, получим
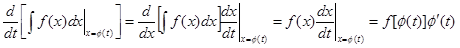 .
.
Отсюда следует, что левая часть равенства (1.2) является неопределенным интегралом по переменной t от функции  , то есть совпадает с правой частью этого равенства. Формула (1.2) может быть записана и так:
, то есть совпадает с правой частью этого равенства. Формула (1.2) может быть записана и так:
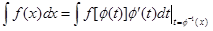 ,
,
где функция 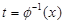 обратная функции
обратная функции  .
.
Замена переменной в неопределенном интеграле 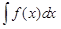 во многих случаях позволяет свести его к более простому или даже табличному интегралу по переменной t, найти его и затем вернуться к переменной x.
во многих случаях позволяет свести его к более простому или даже табличному интегралу по переменной t, найти его и затем вернуться к переменной x.
|
|
|
Примеры
а. Линейная замена переменной
Пример 1. Найти 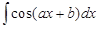 (
(  ).
).
Решение. Введем переменную 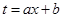 . Тогда
. Тогда  , откуда
, откуда 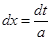 . Используя формулу замены переменной (1.2) и табличный интеграл (VI), получаем
. Используя формулу замены переменной (1.2) и табличный интеграл (VI), получаем
 .
.
Пример 2. Найти 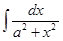 .
.
Решение. Положим 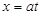 . Тогда
. Тогда 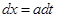 . Используя формулу замены переменных (1.2) и табличный интеграл (X), получим
. Используя формулу замены переменных (1.2) и табличный интеграл (X), получим
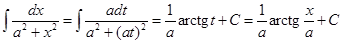 ,
,
так что мы можем записать табличный интеграл (X) в более общем виде:
X. 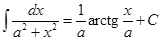 .
.
Аналогично получается табличный интеграл (IX):
IX. 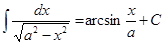 .
.
б. Замена переменной, приводящая к логарифму
Если надо проинтегрировать дробь 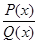 , производная знаменателя которой
, производная знаменателя которой 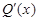 лишь постоянным множителем отличается от числителя P(x), то замена Q(x) = t приведет к табличному интегралу (III).
лишь постоянным множителем отличается от числителя P(x), то замена Q(x) = t приведет к табличному интегралу (III).
Пример 3. Найти  .
.
Решение. Имеем  . Положим
. Положим 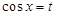 . Тогда
. Тогда  и
и 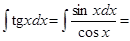
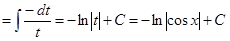 .
.
в. Степенная замена
Пример 4. Вычислить 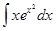 .
.
Решение. Положим 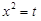 . Тогда
. Тогда 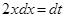 , откуда
, откуда 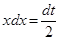 . По формуле замены переменной (1.2), используя табличный интеграл (IV), получим
. По формуле замены переменной (1.2), используя табличный интеграл (IV), получим
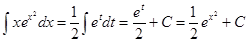 .
.
Интегрирование по частям
Пусть  и
и  – непрерывно дифференцируемые функции на некотором промежутке. Тогда дифференциал их произведения равен
– непрерывно дифференцируемые функции на некотором промежутке. Тогда дифференциал их произведения равен 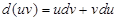 . Интегрируя это равенство по переменной x, получим
. Интегрируя это равенство по переменной x, получим 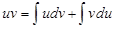 , откуда
, откуда
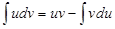 . (1.3)
. (1.3)
Это равенство называется формулой интегрирования по частям. Она позволяет нахождение одного интеграла свести к нахождению более простого интеграла. Рассмотрим два класса функций f(x), которые целесообразно интегрировать по частям, и укажем, что в этих случаях при представлении подынтегрального выражения f(x)dx в виде произведения udv следует брать в качестве u, а что в качестве dv. Ниже через P(x) обозначен многочлен.
|
|
|
I. 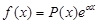 . Следует полагать
. Следует полагать  .
.
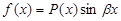 . Следует полагать
. Следует полагать 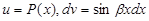 .
.
 . Следует полагать
. Следует полагать  .
.
II. 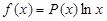 . Следует полагать
. Следует полагать 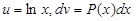 .
.
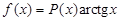 . Следует полагать
. Следует полагать  .
.
 . Следует полагать
. Следует полагать 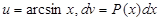 .
.
Пример 1. Найти 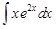 .
.
Решение. Положим u = x, 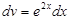 . Тогда
. Тогда 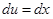 ,
, 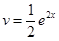 и по формуле интегрирования по частям получим
и по формуле интегрирования по частям получим
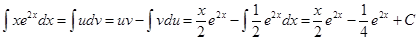 .
.
Пример 2. Найти 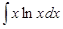 .
.
Решение. Положим 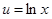 ,
,  .
.
Тогда 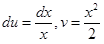 и по формуле интегрирования по частям будем иметь
и по формуле интегрирования по частям будем иметь
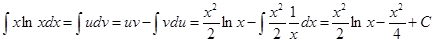 .
.
Дата добавления: 2018-09-23; просмотров: 189; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
