Основные свойства определенного интеграла
1. 
(ибо при 
любая интегральная сумма равна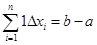 
).
2. Линейность определенного интеграла. Для любых двух интегрируемых на отрезке [a, b] функций f(x) и g(x) и любых чисел l и m справедливо равенство
. (2.2)
Действительно, пусть разбиение отрезка [a, b] на отрезки 
и точки 
i = 1,…,n, будут общими для всех трех интегралов в равенстве (2.2). Тогда для интегральных сумм этих интегралов, как для сумм из конечного числа слагаемых, справедливо равенство
.
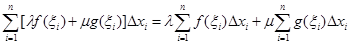Переходя в этом равенстве к пределу при 
, получим доказываемое утверждение.
3. Аддитивность определенного интеграла по области интегрирования. Если отрезок [a, b] разбит точкой c на два отрезка [a, c] и [c, b] и f(x) интегрируема на отрезке [a, b], то
. (2.3)
Действительно, так как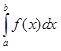 
не зависит от способа разбиения отрезка [a, b] на n частей, то можно рассматривать лишь те разбиения, для которых точка c входит в число точек деления. Тогда это разбиение отрезка [a, b] порождает разбиения отрезков [a, c] и [c, b]: 
и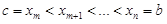 
и справедливо равенство
.
Переходя в этом равенстве к пределу при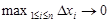 
и учитывая, что при этом будет также 
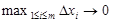и 
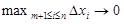, получим доказываемое утверждение.
Следствие. Равенство (2.3) справедливо при любом расположении трех точек a, b, c. Действительно, в случае a < b < c по доказанному имеем
,
откуда
.
Доказательство в остальных четырех случаях аналогично.
|
|
|
Следующие два свойства могут быть доказаны подобно тому, как доказывались свойства 1 и 2.
4. Монотонность определенного интеграла. Если функции f(x) и g(x) интегрируемы на отрезке [a, b] и 
для любых 
, то
. (2.4)
5. Оценка модуля интеграла. Если функция f(x) интегрируема на отрезке [a, b], то
. (2.5)
Для непрерывной на отрезке [a, b] функции f(x) из свойств 1, 4 и 5 вытекает
следствие: 
. (2.5’)
6. Теорема о среднем. Если f(x) непрерывна на отрезке [a, b], то существует по крайней мере одна точка 
на отрезке [a, b] такая, что
. (2.6)
Доказательство. Пусть 
, так что 
для любых 
. Тогда, в силу монотонности и линейности определенного интеграла, имеем
и, деля на (b – a), получаем
.
Так как непрерывная на отрезке функция принимает все промежуточные значения между наименьшим и наибольшим, то найдется по крайней мере одна точка 
на отрезке [a, b] такая, что
,
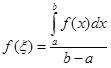откуда следует доказываемое равенство (2.6).
Геометрический смысл теоремы о среднем. Для непрерывной на отрезке [a, b] неотрица-тельной функции f(x) найдется на отрезке [a, b] по крайней мере одна точка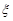 
такая, что криволи-нейная трапеция aABb равновелика прямоугольнику, основанием которого служит отрезок [a, b],
а высота равна значению функции 
(рис. 2).
|
|
|
Рис. 2
Интеграл с переменным верхним пределом, его непрерывность и дифференцируемость. Формула Ньютона–Лейбница
Интеграл с переменным верхним пределом
В этом параграфе установим связь определенного интеграла с неопределенным. Введя понятие интеграла с переменным верхним пределом, мы покажем, что в случае, когда подынтегральная функция непрерывна, он является первообразной этой функции.
Предварительно заметим, что: 1) определенный интеграл как предел интегральных сумм не зависит от того, какой буквой обозначается переменная интегрирования: 
;
2) функция, интегрируемая на отрезке [a, b], будет интегрируема и на отрезке [a, x] при любом 
.
Пусть f(x) непрерывна на отрезке [a, b]. Для любого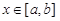 
положим 
.
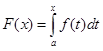(Здесь для того чтобы подчеркнуть, что функция F(x) является функцией переменного верхнего предела, переменная интегрирования обозначена другой буквой.)
Докажем, что:
1) F(x) непрерывна на отрезке [a, b];
2) F(x) дифференцируема в каждой точке интервала (a, b) и 
(производная интеграла по переменному верхнему пределу равна значению подынтегральной функции от значения аргумента, равного верхнему пределу).
|
|
|
Дадим аргументу x приращение Dx такое, что 
, и найдем соответствующее приращение функции F(x):
.
Используя свойство аддитивности определенного интеграла и теорему о среднем, получим
,
где точка расположена между точками x и x + Dx. При 
имеем 
, и в силу непрерывности функции f(x) будет 
. Тогда:
1) 
и, следовательно, F(x) – непрерывная функция на отрезке [a, b];
2) 
,
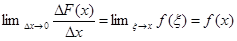то есть F(x) – дифференцируемая функция и 
.
Таким образом, всякая непрерывная на отрезке [a, b] функция f(x) имеет первообразную, равную интегралу 
, и тогда согласно определению неопределенного интеграла имеет место равенство
.
Формула Ньютона–Лейбница
Пусть функция f(x) непрерывна на отрезке [a, b]. Если функция F(x) – первообразная функции f(x), то
(формула Ньютона-Лейбница).
Доказательство. Наряду с F(x) первообразной функции f(x) является функция 
. А так как всякие две первообразные одной и той же функции отличаются на константу, то справедливо равенство
. (2.7)
|
|
|
Полагая в этом равенстве сначала x = b, а затем x = a, получим
,
.
Вычитая из первого равенства второе, получим формулу Ньютона–Лейбница. Разность 
в правой части этой формулы записывают также в виде 
.
Пример. Вычислить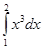 
.
Решение. Имеем
.
Дата добавления: 2018-09-23; просмотров: 500; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!