Методы интегрирования некоторых тригонометрических и иррациональных выражений
В этом параграфе для интегралов от некоторых классов тригонометрических и иррацио-нальных выражений будут даны рационализирующие подстановки, то есть замены переменной, приводящие исходный интеграл к интегралу от рациональной дроби. Ниже через 
будем обозначать рациональные функции своих аргументов.
I. 
.
Интегралы от выражений, рационально зависящих от sinx и cosx, всегда сводятся к интегралу от рациональной дроби универсальной подстановкой:
.
Действительно:
,
,
, 
.
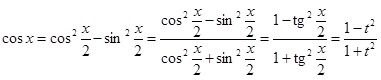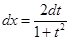Подставляя в подынтегральное выражение вместо sinx, cosx и dx их выражения через t и dt, получим интеграл от рациональной дроби (формулу интегрирования тригонометрических выражений):
.
Пример
.
Однако в частных случаях предпочтительнее использование других подстановок, которые приводят к интегрированию более простых рациональных дробей, чем при использовании универсальной подстановки. А именно:
а) если подынтегральная функция нечетна относительно sinx, то есть при замене sinx на –sinx она лишь меняет знак, то делают подстановку cosx = t;
б) если подынтегральная функция нечетна относительно cosx, то есть при замене cosx на –cosx она лишь меняет знак, то делают подстановку sinx = t;
в) если подынтегральная функция при замене одновременно и sinx, и cosx на –sinx и –cosx не меняется, то делают подстановку tgx = t.
Примеры:
1. Найти 
.
Решение. Подынтегральная функция меняет знак при замене cosx на –cosx (имеет место случай б). Используем замену переменной sinx = t. Тогда 
, 
и
.
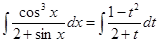Интегрируя, получим
.
Возвращаясь к переменной x, будем иметь
.
2. Найти 
.
Решение. Подынтегральная функция при замене sinx и cosx на –sinx и –cosx не меняется (имеет место случай в). Используем замену переменной tgx = t. Тогда 
, 
,
и
.
II. 
, где m, n – целые неотрицательные числа. К этим интегралам применяют так называемый метод понижения степени: с помощью известных формул из тригонометрии
исходный интеграл преобразуется в сумму интегралов от произведений степеней sin2x и cos2x с меньшими показателями.
Пример
.
III. Интегралы вида
сводятся к табличным с помощью формул:
,
,
.
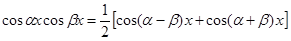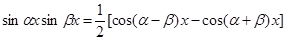Пример
.
IV. Рассмотрим рационализирующие подстановки для интегралов от иррациональных выражений вида
,
где n,…,m – целые числа.
Пусть s – наименьшее общее кратное чисел n,…m. Тогда замена переменной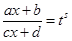 
приведет исходный интеграл к интегралу от рациональной дроби.
Пример.Найти 
.
Решение. Наименьшее общее кратное чисел 2 и 3 равно 6. Положим 
. Тогда 
, 
, 
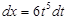и
.
V. Интегралы вида:
а)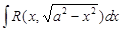 
, б) 
, в) 
тригонометрическими подстановками, соответственно: а) 
, б) 
, в) 
сводятся к уже рассмот-ренным интегралам вида 
.
Пример.
Найти 
.
Решение. Положим 
. Тогда 
, 
и исходный интеграл преобразуется в интеграл 
вида II. Интегрируя его, получим
.
Возвращаясь к переменной x, окончательно будем иметь
.
(Заметим, что в интеграле 
использование тригонометрической подстановки нецелесообразно, так как гораздо проще интеграл берется с помощью степенной подстановки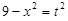 
. Действительно, дифференцируя это равенство, получим 
или 
. Тогда получим
).
К рассмотренным интегралам могут быть преобразованы интегралы 
, если из квадратного трехчлена выделить полный квадрат суммы и сделать линейную замену переменной.
Отметим, что существуют другие методы интегрирования интегралов , которые мы здесь не рассматриваем.
Определенный интеграл
2.1. Определение определенного интеграла, условия его существования.
Свойства определенного интеграла
Дата добавления: 2018-09-23; просмотров: 245; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!